This is going to be the first of a series of commentary posts on the types of problems that I help teachers learn to use to teach math with problem-based learning.  The type of PBL that I am a supporter of is what I call Relational Problem-Based Learning in which the construction of knowledge comes from the discussion of scaffolded problems.  I’ll give specific examples of the problems that the students and teacher discuss and the ways in which the discussion builds on prior knowledge.

A great example of this is the way that the Pythagorean Theorem and the concept of Pythagorean Distace are connected so nicely. The prior knowledge that is assumed (and triggered with basic problems of finding legs, hypotenuses, simplifying radicals, etc.) is basic use of the Pythagorean Theorem.

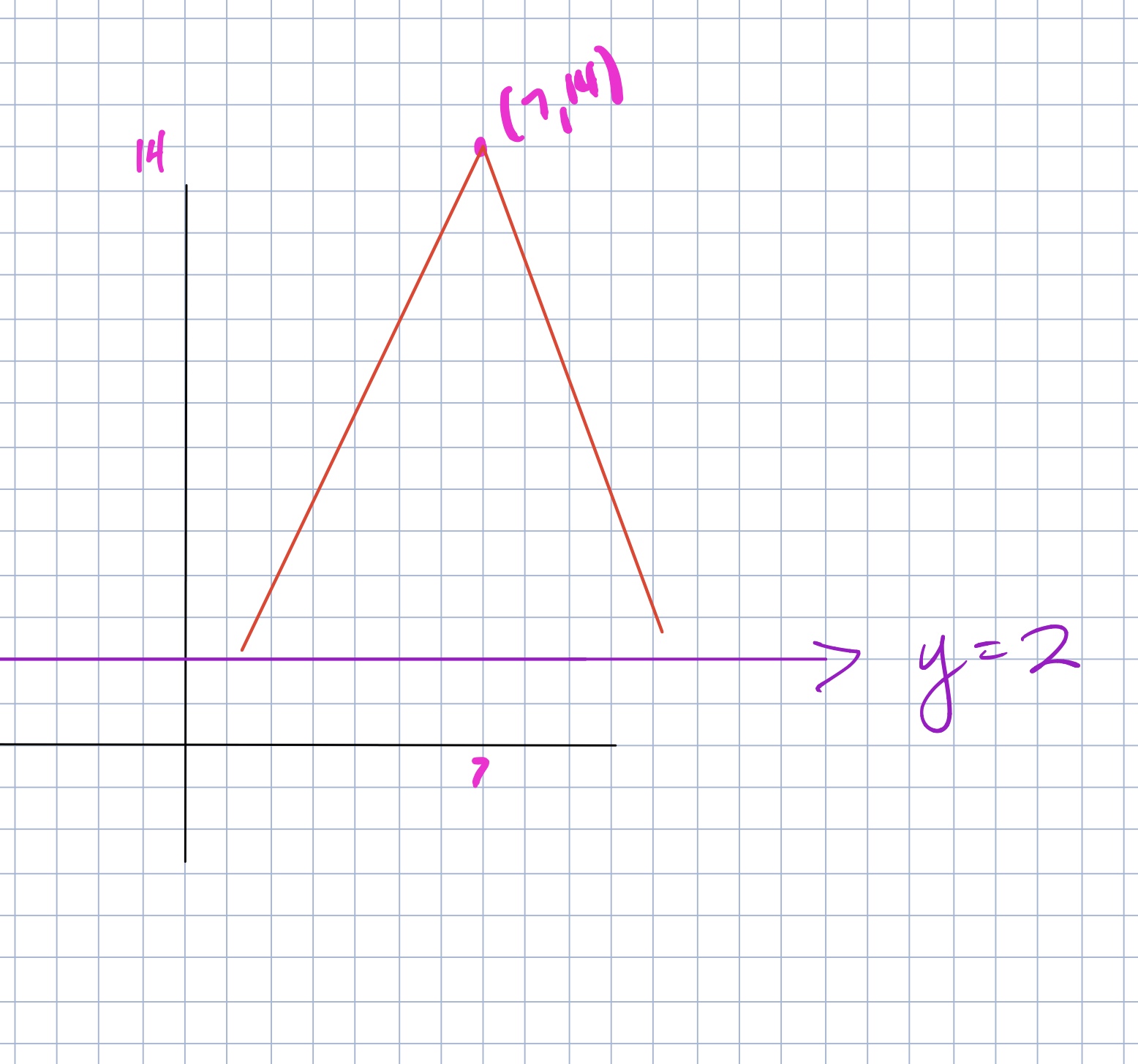
Number 9 in the Avenues Math 2 book (adapted from the PEA Materials) says:

Two different points on the line y = 2 are each exactly 13 units from the point (7, 14). Draw a picture of this situation, and then find the coordinates of these points.

This problem is usually done within the first week or so of school. When doing this problem for homework without having previously discussed something like this in class, many students are capalble of graphing the line y=2 (although you can probably guess the most common error!) and the point (7,14).  However, many students often are still confused about what the distance “13 units” means. Many student come to class with something like this, which is a totally acceptable attempt actually.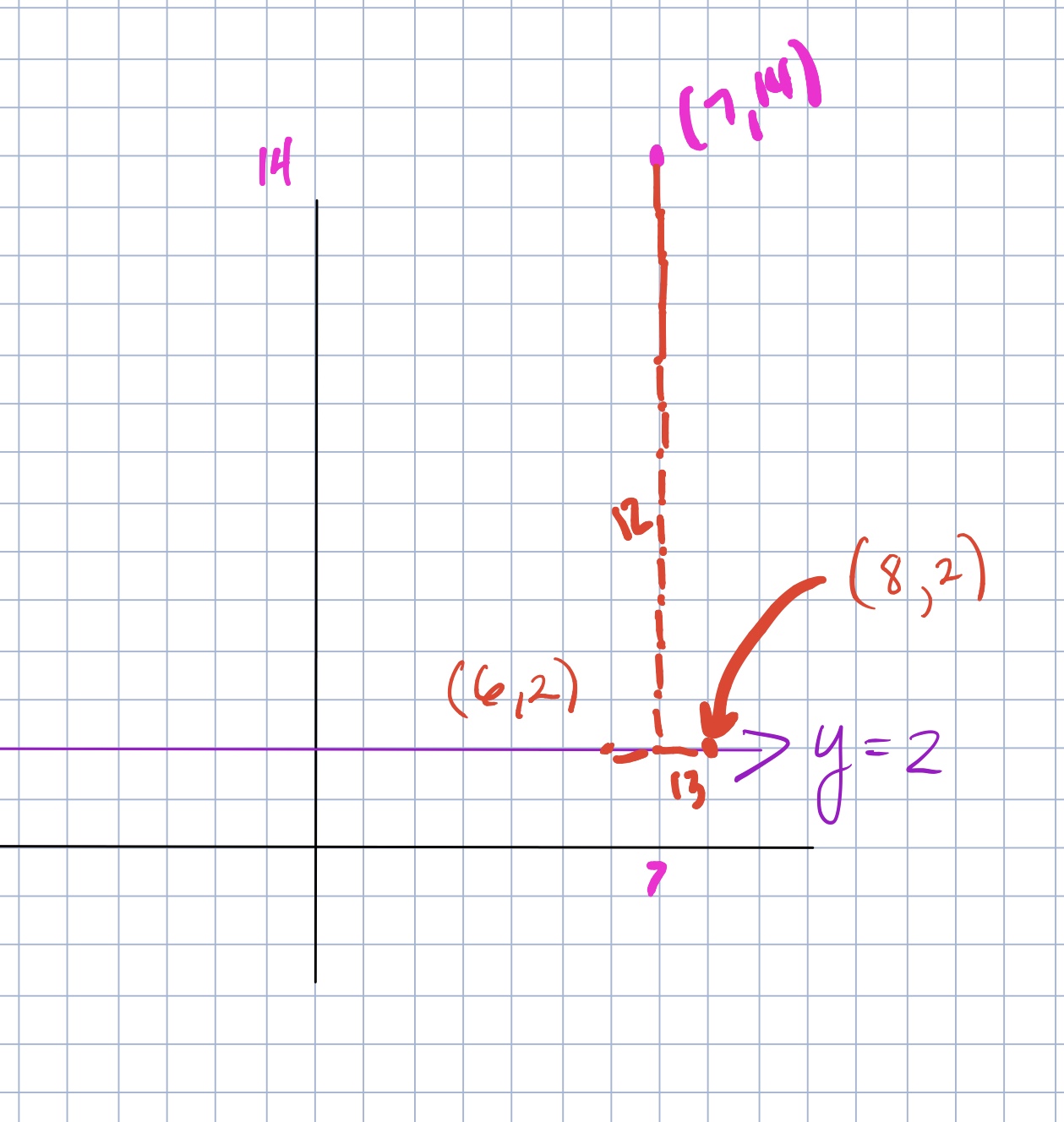

This first attempt is a great conversation starter about what Pythagorean distance in the geometry that we are studying means.  In fact for any kids who live in a city, it’s a great opportunity to talk about “Taxi-Cab” Geometry and how that is a different way of measuring distance.  The interesting thing is that many students who come to class with this type of inital definition of distance oftentimes live in a city.  I find it really important to validate their idea of distance but just to say that it’s just not the Pythagorean Definition of distance and if they want to learn more about Taxi-Cab Distance, I have readings on it. (see here and here).  This is consistent with Chris Emdin’s opening talk at the NCTM annual this year about privileging all students intuition about math.

Generally, the discussion that follows is that some other students says that they did not think of the distance that way.  They saw it “straight” there.  If not other students says this, which is usually rare, but could happen, Then it is the teachers responsibility to bring up the idea of a more direct distance.  What I usually do is ask “What other ways are there to think about distance?” Some student usually says something like “as the crow flies” or “straight there” – which is really funny.  They have the idea but don’t really know how to say what they mean.

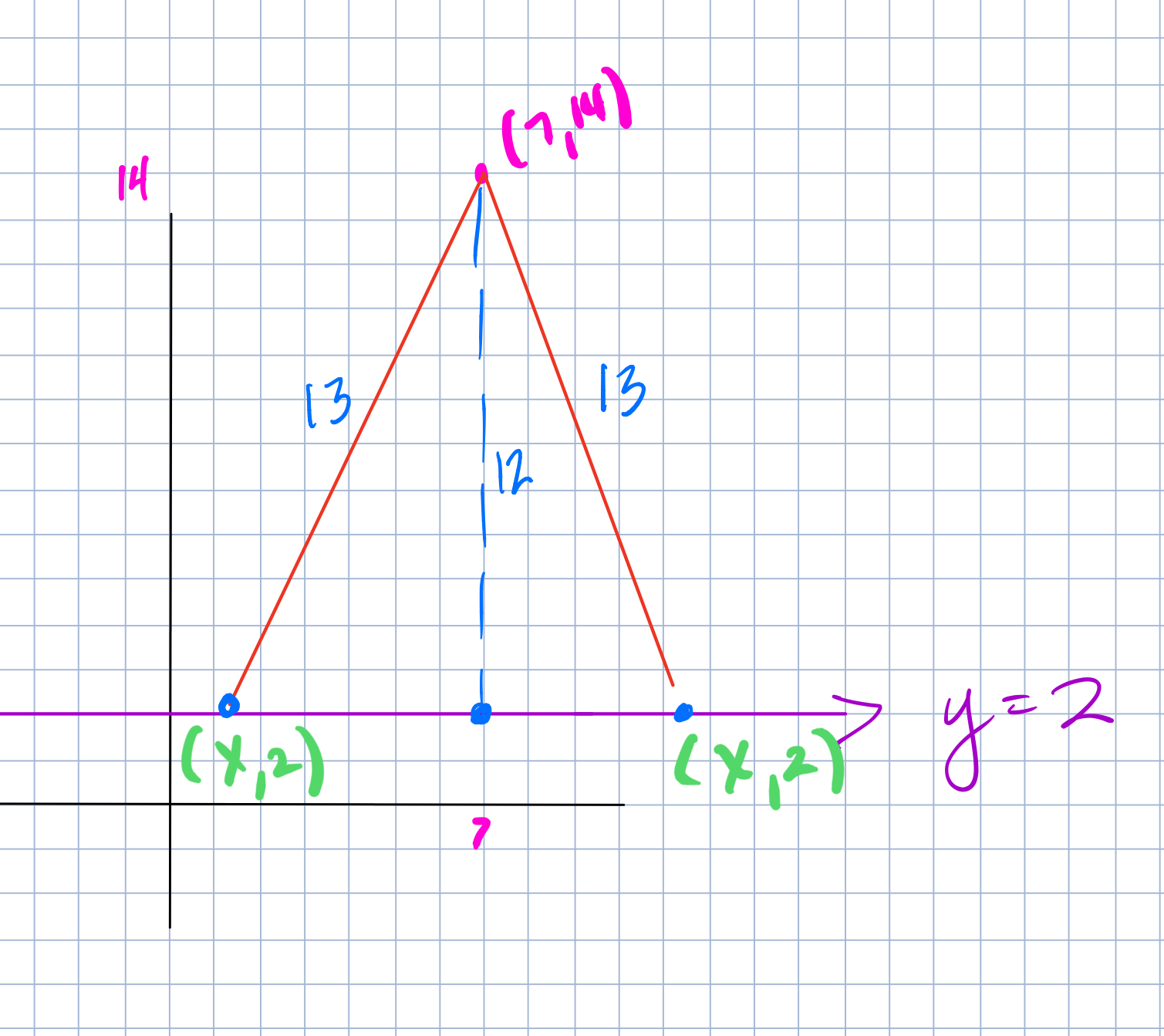
They can sometimes draw a picture like this:

But the idea that they need to figure out the coordinates that are on the line y=2 is very difficult.  The students don’t know where to put the points there on the line y=2, so it’s hard for them to label them – what do they do?  At this point, if a student can’t say that the distance is supposed to be 13.  They need a question that is leading them to the right direction.  A few different directions can be taken:

1. Ask the students if the fact that the vertical direction was 12 is helpful at all – that was something that a student realized and is actually important to the solution of the problem.
2. Ask the students where the distance that is supposed to be 13 is represented in the diagram they’ve drawn now
3. have the students turn and talk to each other to think about ways in which they might visualize the “two different points that are 13 units away”

In my experience, what follows from these teacher actions is some productive struggle, as long as you are patient.  When students get to this point:

The next difficulty is figuring out the coordinates.  This is where the Pythagorean Theorem comes in.  Even if the students can see the 12 and the 13, it might be difficult for them to get to the point where they realize that there is a right triangle in the diagram.  This should be a whole class conversation in order to optimize the likelihood of a student seeing the right angle.  Finding the missing side, does not even guarantee being able to find the coordinates.

So in order to have students to be able to add and subtract 5 from 7, students need to be able to have the coordinates of the point that is directly below (7,14) on the line y=2, which is (7,2).  I always try my hardest not to just come out and ask “What are the coordiantes of the point right below (7,14) becasue that is just basically telling them what they need to find.  I try to ask them what do they need to know in order to find the coordinates.

It is very satisfying when students finally see that it is really just an application of the Pythagorean Theorem.  I wrote a blogpost about one conversation with a student about just this problem a while ago.

Just another note on alternate perspectives:  I have had students do this by looking at this problem as a circle intersecting the line y=2.  Of coruse, they don’t know how to do that right now, but students who are technologically savvy end up doing in on geogebra and having stuch a great concept of what 13 units away means that they get the right answers without using the Pythagorean theorem.. It is a great way to try to get students to even see that the “radius” they are using is the hypotenuse of a right triangle.