Tag: PBLCurricula

Teaching Circle Concepts with PBL

In a traditional Geometry text, there is a chapter on circles – usually around 8 or 9 – right? Where they introduce a definition, the equation in a big blue box and students learn how to write equations, find the area, circumference and do some interesting problems negative space if they are lucky.  The question then is how are circles connected to the rest of the geometry curriculum?  There is so much more that students could be able to see that goes unseen when circles are compartmentalized like this.  Circles are often introduced in middle school mathematics classes and by the time they get to high school geometry students have seen area and circumference and perhaps even understand a little bit of the irrationality of pi.  What then can a PBL curriculum do to help students understand circle concepts more deeply and in a more connected way?

One of the first types of problems that students are asked to do in the curriculum that I have adapted goes like this:

Find two lattice points that are 5 units away from each other that are not horizontal nor vertical.

This question is clearly asking for two integer-values points on the coordinate plane that are 5 units from each other but students can’t just count them since the distance is diagonal.  This is often a difficult idea for students at first who are not comfortable with the idea of Pythagorean distance (see previous post about Pythagorean distance).  However, since the beginning of the Math 2 book has so much work with the Pythagorean Theorem, it may be that students are thinking of the distance as the hypotenuse of a right triangle and can think of the 3-4-5 that has shown up in many other problems.  It does take some time for students to be able to think of two points like (1,2) and (4,6) as 5 units away from each other.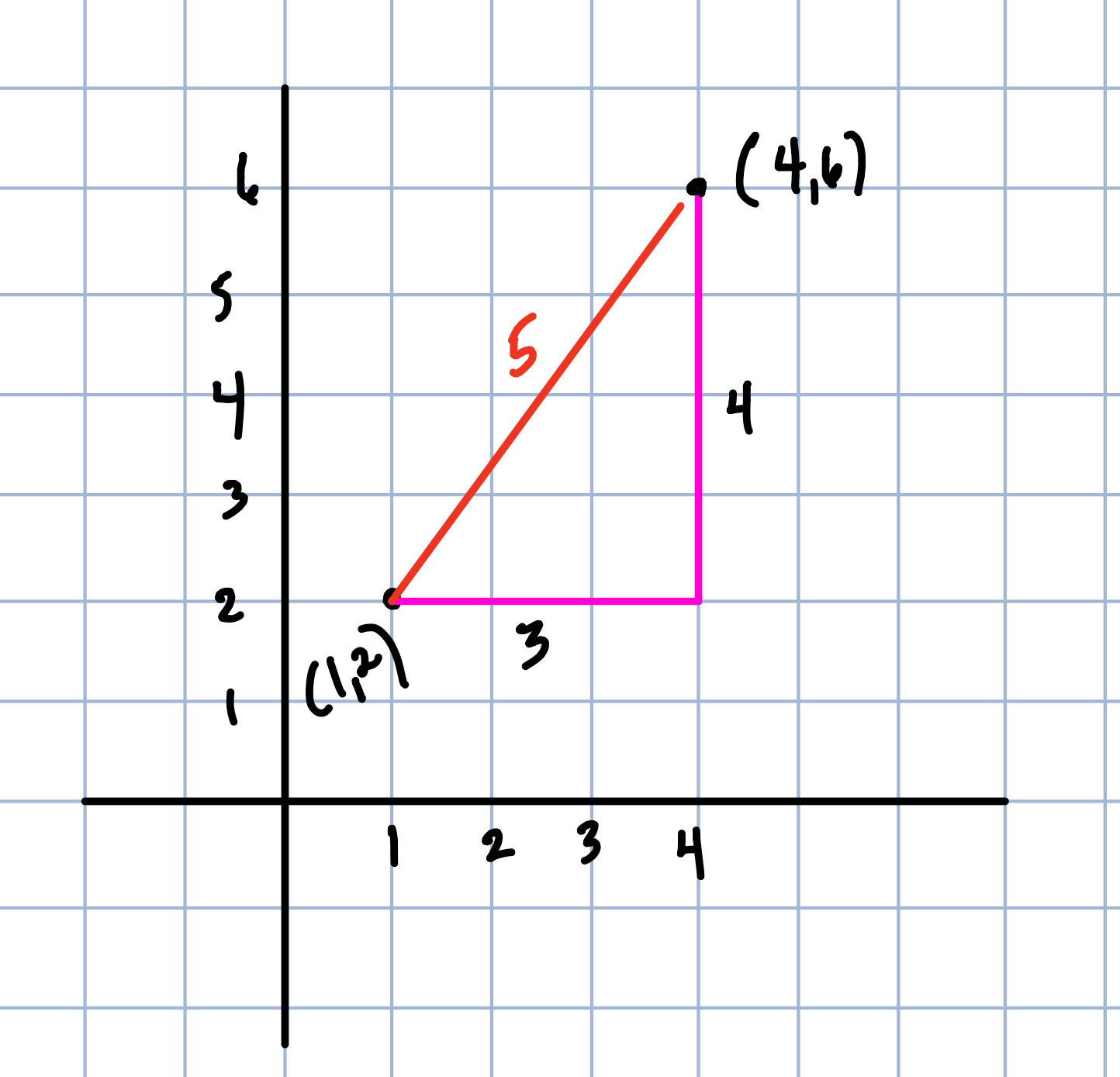

Students are asked other questions about the configuration of points that meet certain criteria and how it would be represented algebraically.  For example:

Describe the set of points that are all 3 units away from the x-axis.  How would you describe this configuration in an equation?

This is trying to get students used to visualizing ALL points that satisyfing a given distance condition and when other conic sections are discussed in later courses, they are prepared to be thinking of configurations as a set of points.  So finally when they are asked to

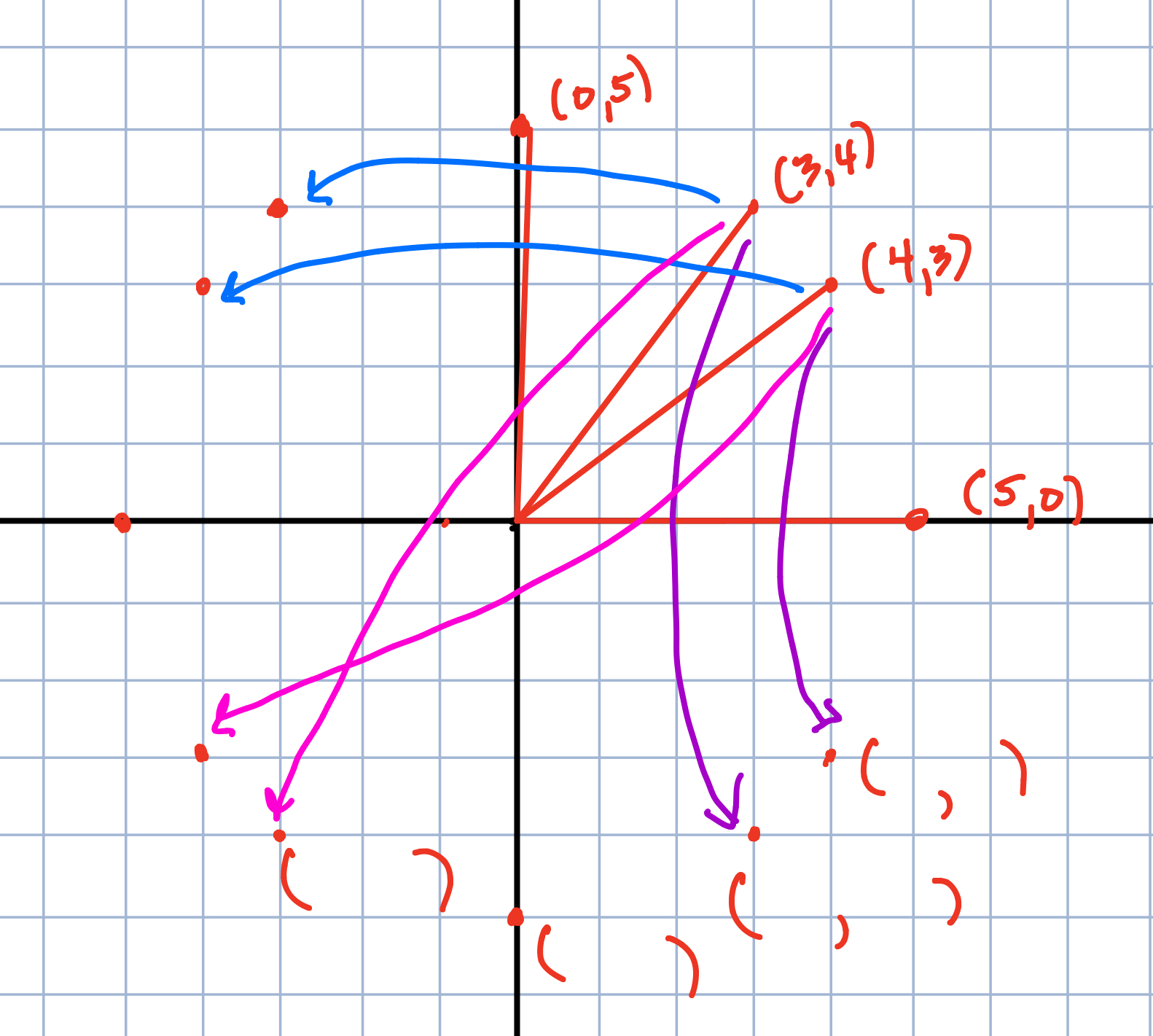
Write an equation using the distance formula that says that P=(x,y) is 5 units from (0,0).  Plot several such points.  What is the configuration of all such points called? How many are lattice points?  [See here for a wonderful journal entry by a student on this question].

This question is the first time that circles are actually introduced and the word “circle” isn’t even in the problem.  The discussion that occurs can be very deep and interesting (as is what happened when the student who wrote that journal entry presented this problem) or it could be very straightforward and benign.  I have been impressed over the year with how well some students understand that a circle must contain points that are all the same distance from the point that is the center.  It is introduced with the distance formula because so much of their work to the point has been based on the distance formula.

Students have a great time discussing the number of lattice points that lie on the circle and where they are.  If they can harken back to the earlier problem about points that are 5 units apart, they recall the 3-4-5 right triangle easily and get the lattice points in the first quadrant.

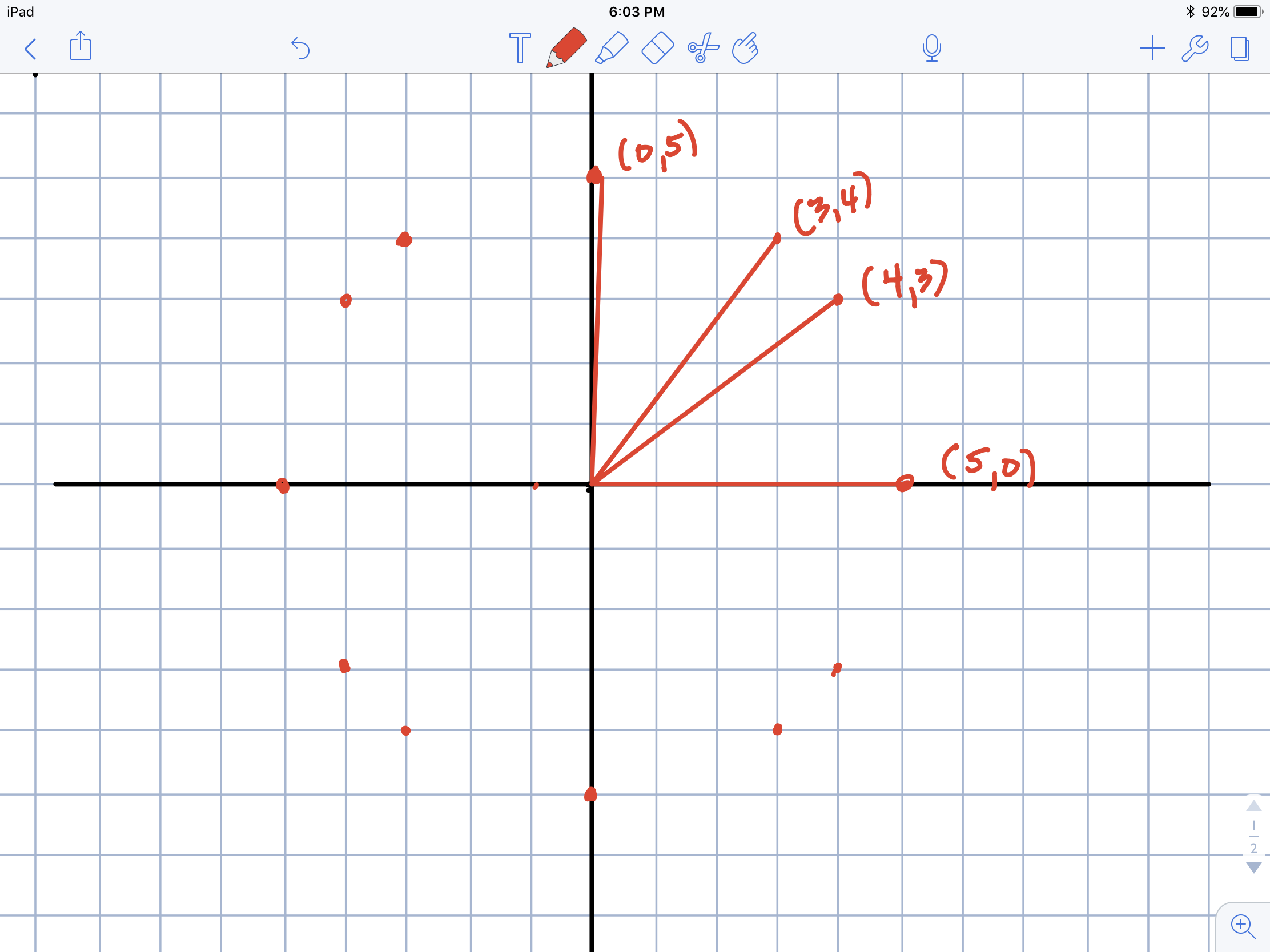
Most students can then use their knowledge of transformations and the symmetry that the circle has and find the coordinates of the of the other lattice points.  This is also a wonderful conversation about reflection over the axes or origin.

 

If the student presenting this problem leaves the equation in the distance formula form without simplifying, that’s even better and sets up the next question:

Explain how you could use the Pythagorean Theorem to obtain the same result.

At this point, it is important to connect the distance of five units, the center of the origin and the idea of the radius being a hypotenuse of a right triange with the coordinates the students just found.  This will be so important later on when students work with the unit circle in trigonometry for thefirst time.

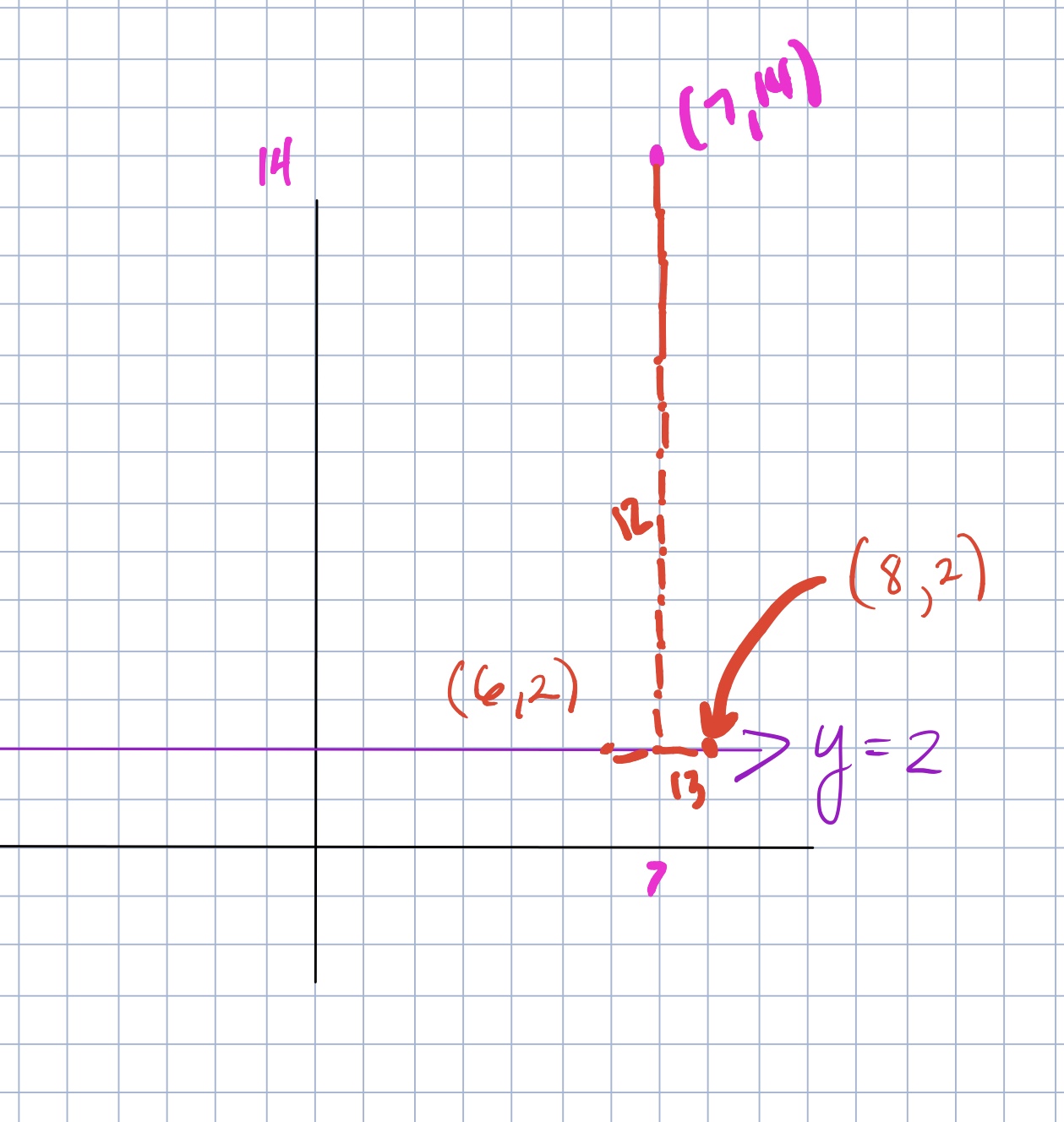
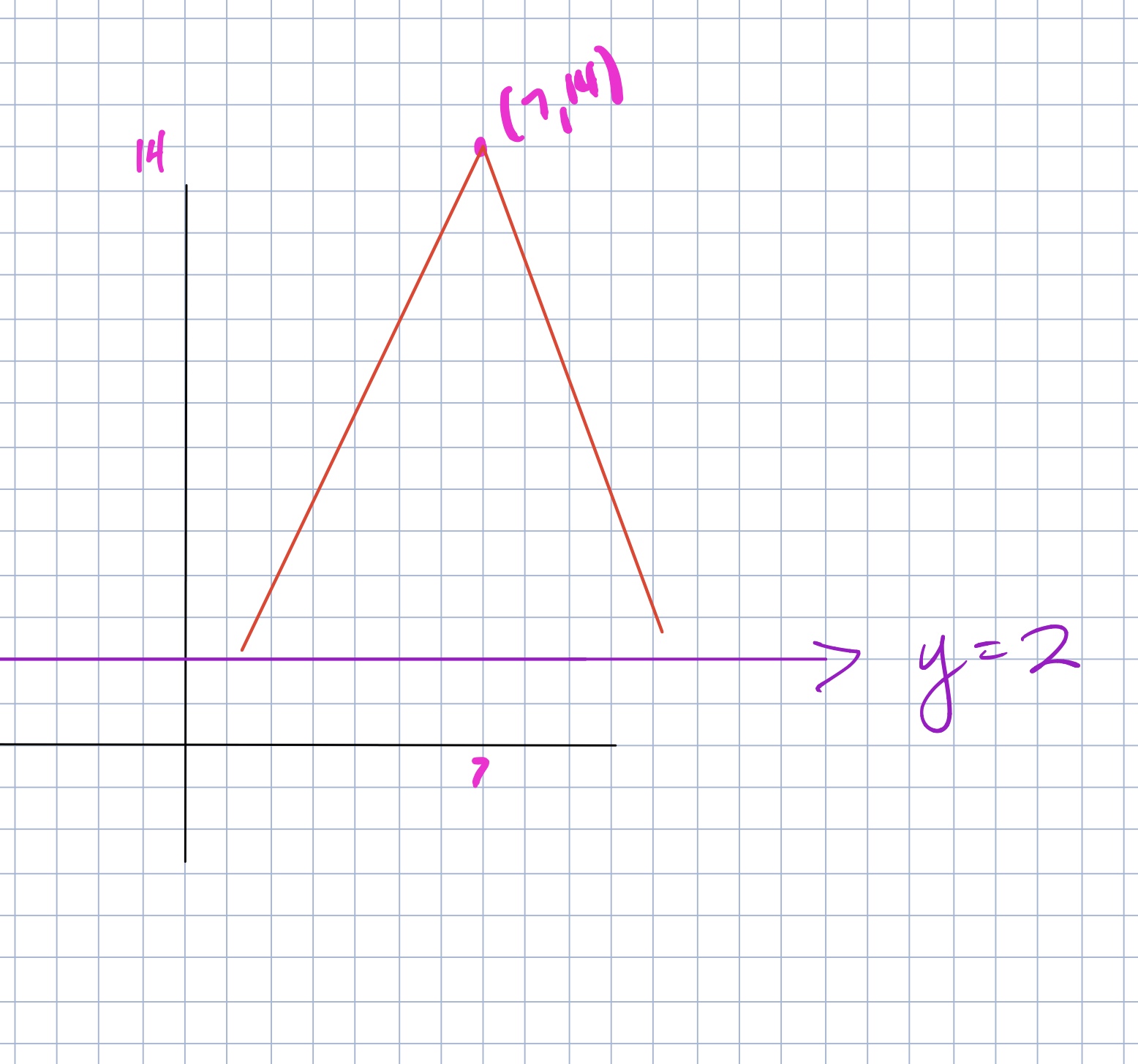
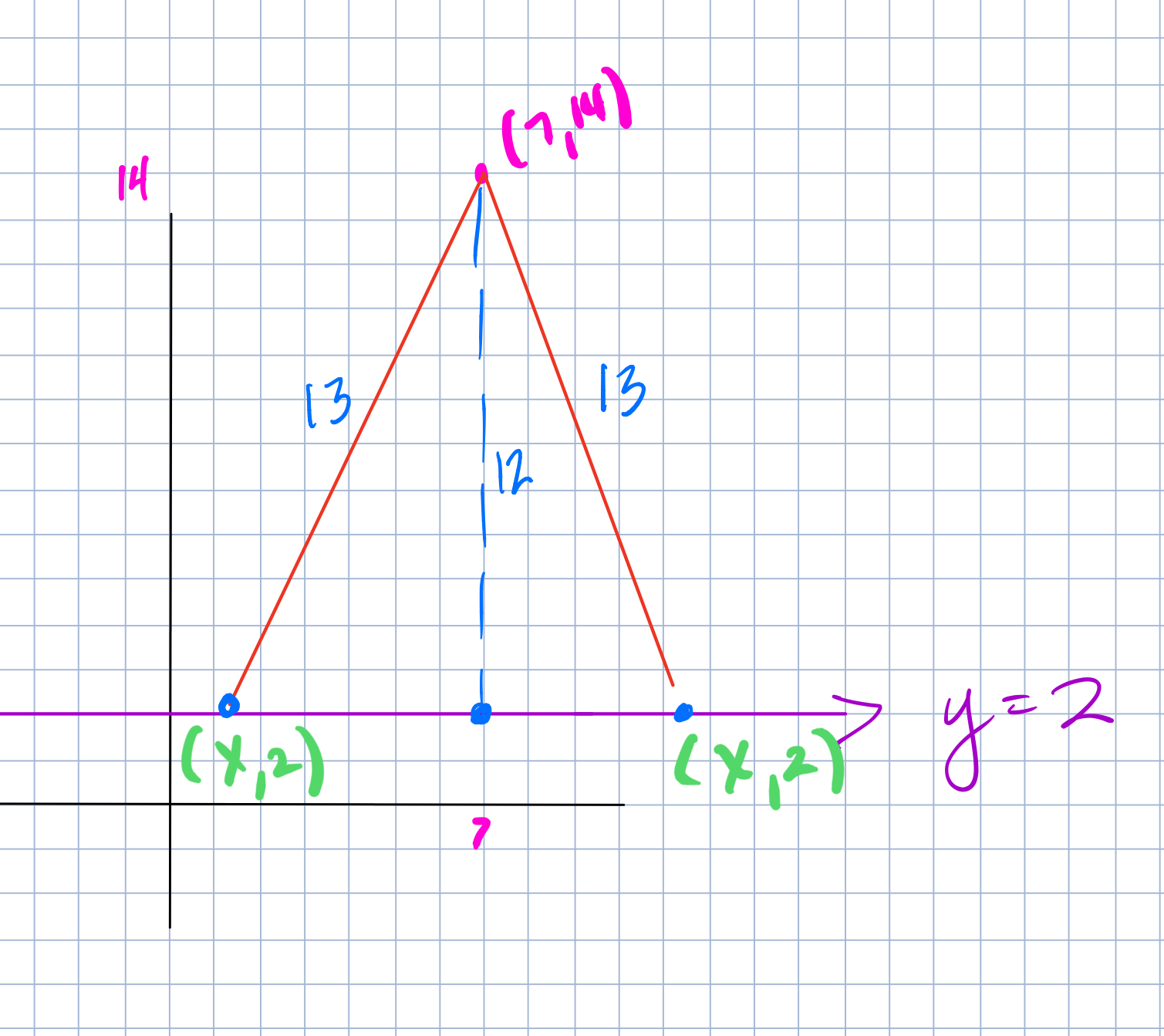
Ask students to start by drawing right triangles where they think they might be in the circle.  Interestingly (and maybe obviously) many of them try to draw it like this (see below) where the right angle is at the origin.  This is a great time for a conversation about where the points are that are “5 units away from the origin,” where that distance is, and which point are they saying is on the circle with the right triangle.  If some student can connect the idea that the radius is supposed to be the hypotenuse and let another student co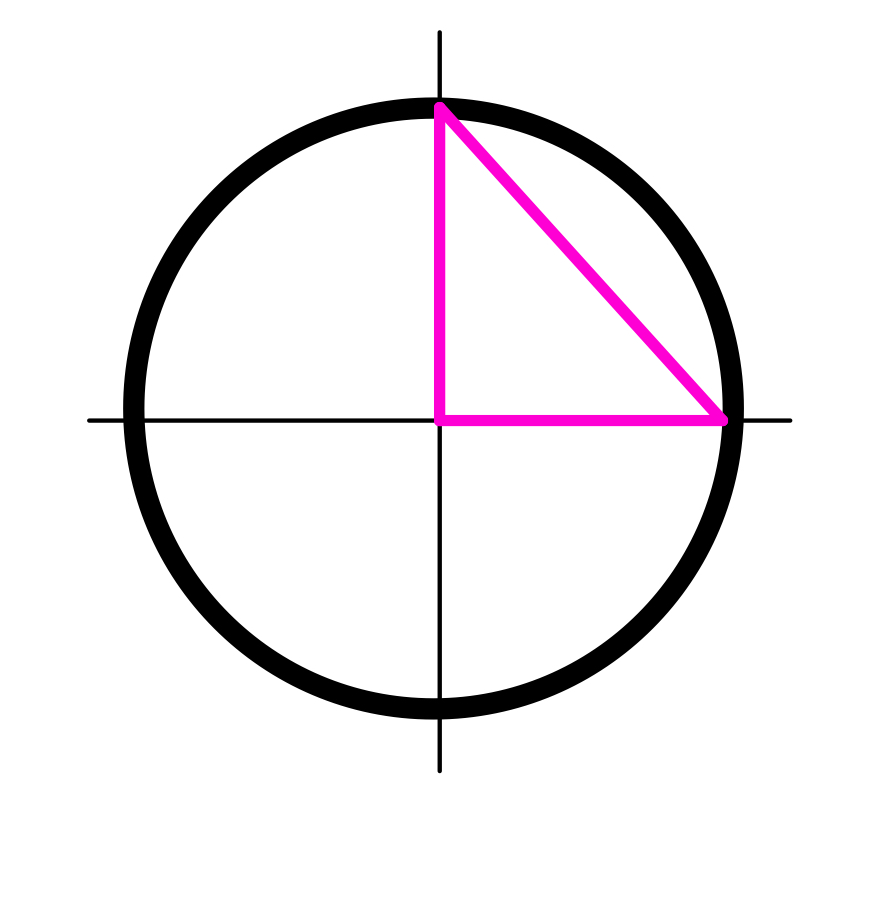me up to the board and make an attempt at the drawing, it is much better than the teacher drawing it for them.  As the discussion moves forward and a student can draw the correct right triangle, I have always tried to get other students to draw other triangles.  The first that usually happens is that students generally draw the right triangles that have the lattice points as the point on the circle.  It takes some time for students to think about the idea that (x, y) can be any point such that x²+y²=25.  This takes some time and discussion.

With a group that is ready, I have also asked students to find the y-coordinates that corresponds to the point on the circle that has the x coordinate that is equal to 1 or 2 and see what they come up with.  This is a great time to see if they truly understand what the equation is telling them.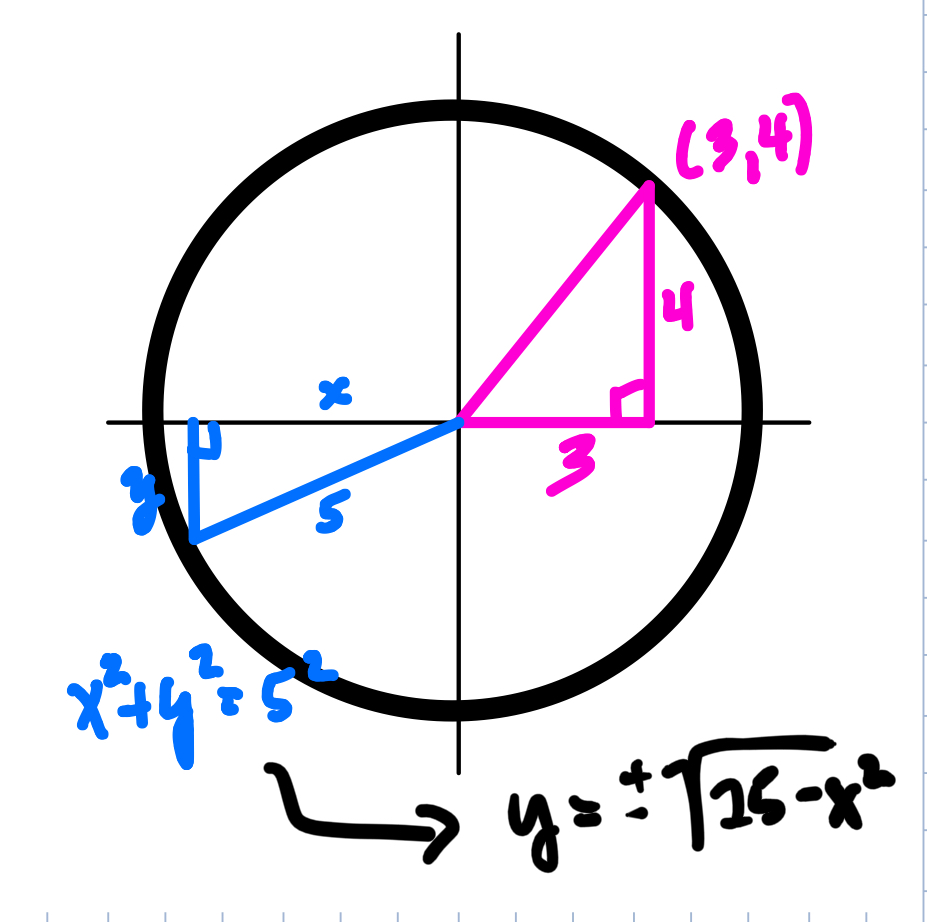

There are many more problems that come after this – some ask for what circles have in common from their equations, some ask for lengths of chords, some are area and circumference problems.  I will write another post on how inscribed angles and arcs are introduced but the idea that circles are all connected to the distance formula and the Pythagorean Theorem is a deep one that runs through the whole curriculum and is important for students to see the connections between the right triangles and the circle itself.

Teaching Pythagorean Distance with PBL

This is going to be the first of a series of commentary posts on the types of problems that I help teachers learn to use to teach math with problem-based learning.  The type of PBL that I am a supporter of is what I call Relational Problem-Based Learning in which the construction of knowledge comes from the discussion of scaffolded problems.  I’ll give specific examples of the problems that the students and teacher discuss and the ways in which the discussion builds on prior knowledge.

A great example of this is the way that the Pythagorean Theorem and the concept of Pythagorean Distace are connected so nicely. The prior knowledge that is assumed (and triggered with basic problems of finding legs, hypotenuses, simplifying radicals, etc.) is basic use of the Pythagorean Theorem.

Number 9 in the Avenues Math 2 book (adapted from the PEA Materials) says:

Two different points on the line y = 2 are each exactly 13 units from the point (7, 14). Draw a picture of this situation, and then find the coordinates of these points.

This problem is usually done within the first week or so of school. When doing this problem for homework without having previously discussed something like this in class, many students are capalble of graphing the line y=2 (although you can probably guess the most common error!) and the point (7,14).  However, many students often are still confused about what the distance “13 units” means. Many student come to class with something like this, which is a totally acceptable attempt actually.

This first attempt is a great conversation starter about what Pythagorean distance in the geometry that we are studying means.  In fact for any kids who live in a city, it’s a great opportunity to talk about “Taxi-Cab” Geometry and how that is a different way of measuring distance.  The interesting thing is that many students who come to class with this type of inital definition of distance oftentimes live in a city.  I find it really important to validate their idea of distance but just to say that it’s just not the Pythagorean Definition of distance and if they want to learn more about Taxi-Cab Distance, I have readings on it. (see here and here).  This is consistent with Chris Emdin’s opening talk at the NCTM annual this year about privileging all students intuition about math.

Generally, the discussion that follows is that some other students says that they did not think of the distance that way.  They saw it “straight” there.  If not other students says this, which is usually rare, but could happen, Then it is the teachers responsibility to bring up the idea of a more direct distance.  What I usually do is ask “What other ways are there to think about distance?” Some student usually says something like “as the crow flies” or “straight there” – which is really funny.  They have the idea but don’t really know how to say what they mean.

They can sometimes draw a picture like this:

But the idea that they need to figure out the coordinates that are on the line y=2 is very difficult.  The students don’t know where to put the points there on the line y=2, so it’s hard for them to label them – what do they do?  At this point, if a student can’t say that the distance is supposed to be 13.  They need a question that is leading them to the right direction.  A few different directions can be taken:

  1. Ask the students if the fact that the vertical direction was 12 is helpful at all – that was something that a student realized and is actually important to the solution of the problem.
  2. Ask the students where the distance that is supposed to be 13 is represented in the diagram they’ve drawn now
  3. have the students turn and talk to each other to think about ways in which they might visualize the “two different points that are 13 units away”

In my experience, what follows from these teacher actions is some productive struggle, as long as you are patient.  When students get to this point:

The next difficulty is figuring out the coordinates.  This is where the Pythagorean Theorem comes in.  Even if the students can see the 12 and the 13, it might be difficult for them to get to the point where they realize that there is a right triangle in the diagram.  This should be a whole class conversation in order to optimize the likelihood of a student seeing the right angle.  Finding the missing side, does not even guarantee being able to find the coordinates.

So in order to have students to be able to add and subtract 5 from 7, students need to be able to have the coordinates of the point that is directly below (7,14) on the line y=2, which is (7,2).  I always try my hardest not to just come out and ask “What are the coordiantes of the point right below (7,14) becasue that is just basically telling them what they need to find.  I try to ask them what do they need to know in order to find the coordinates.

It is very satisfying when students finally see that it is really just an application of the Pythagorean Theorem.  I wrote a blogpost about one conversation with a student about just this problem a while ago.

Just another note on alternate perspectives:  I have had students do this by looking at this problem as a circle intersecting the line y=2.  Of coruse, they don’t know how to do that right now, but students who are technologically savvy end up doing in on geogebra and having stuch a great concept of what 13 units away means that they get the right answers without using the Pythagorean theorem.. It is a great way to try to get students to even see that the “radius” they are using is the hypotenuse of a right triangle.