Tag: Boaler

Teaching Students to Become Better “Dancers”

So the other day I read a tweet by Justin Lanier that really sparked my interest.

 We all know the scenario in classroom discourse where a student asks a question – a really great question – and you know the answer, but you hedge and you say something like, “That’s a great question! I wonder what would happen if…”  So you reflect it back to the students so that they have something to think about for a little while longer, or maybe even ask a question like “Why would it be that way?” or “Why did you think or it like that?”  to try to get the student to think a bit more.  But what Justin, and the person who coined the phrase “authentic unhelpfulness” Jasmine Walker (@jaz_math), I believe were talking about was hedging because you really don’t know the answer – sincere interest in the uniqueness of the question – not because you’re so excited that student has helped you move the conversation forward, but because of your own excitement about the possibilities of the problem solving or the extension of the mathematics.

I think what got me so excited about this idea was how it connected to something that I was discussing earlier this summer with a group of teachers in my scaffolding in PBL workshop in late June.  In a PBL curriculum, the need to make sure that students have the right balance of scaffolded problems and their own agency is part of what Jo Boaler called the “Dance of Agency” in a paper she wrote in 2005 (see reference).  My understanding of this balance goes something like this:

(c) Schettino 2013

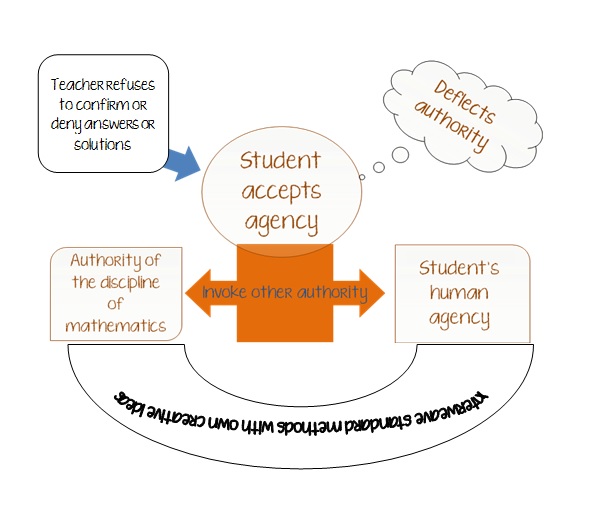
So initially, the student is confused (or frustrated) that the teacher refuses to answer the question although you are giving lots of support, advice and encouragement to follow their instincts.  The student has no choice but to accept the agency for his or her learning at that point because the teacher is not moving forward with any information.  But at that point usually what happens is that a student doesn’t feel like she has the authority (mathematical or otherwise) to be the agent of her own learning, so she deflects the authority to some other place.  She looks around in the classroom and uses her resources to invoke some other form of authority in problem solving.  What are her choices?

She’s got the discipline of mathematics – all of her prior knowledge from past experiences, she’s got textbooks, the Internet, her peers who know some math, other problems that the class has just done perhaps that she might be able to connect to the question at hand with previous methods that she might or might know how they work or when they were relevant – that discipline has had ways in which it has worked for her in the past and lots of resources that can help even if it may not be immediately obvious.

But she’s also got her own human agency which is most often expressed in the form of asking questions, seeing connections, drawing conclusions, thinking of new ideas, finding similarities and differences between experiences and thinking about what is relevant and what is not.  These pieces of the puzzle are not only important but a truly necessary function of the “dance of agency” and imperative to problem solving.

Interweaving both of these types of agency (and teaching kids to do this) have become more important than ever.  Yes, being able to use mathematical procedures is still important, but more important is the skill for students to be able to apply their own human agency to problem and know how and when to use which mathematical procedure, right?  This “dance” is so much more important to have every day in the classroom and if what initiates it is that deflection of authority then by all means deflect away – but the more we can “dance” with them, with “authentic unhelpfulness” and sincere deflection because we need to practice our own human agency, the more we are creating a true community of practice.

Boaler, J. (2005). Studying and Capturing the complexity of practice – the Case of the ‘Dance of Agency’

Linking Theory to Practice: A Shout-Out to ‘savedabol’

This past January, I gave a key-note address at the ISOMA conference in Toronto and posted my slides from that talk on my academia.edu site that I thought would be a good place for me to easily give other people access to my work. (along with my website).  Academia.edu is great because it gives you lots of information about the stats of surfers who come and look at your information.  All of a sudden I saw that this powerpoint had more than something like 400 views and I couldn’t believe it.  I had to see who was searching and looking at this slideshow.

I quickly realized that someone had seen it, liked it and posted something about it on reddit.  There were only a few comments but one of them went something like this:

“I think the single worst part of being a teacher is sitting through PowerPoints like this, while some earnest non-classroom pedagogue tells us the bleeding obvious.”

Whooo – that one stung…my first instinct was to try and find out who that person was and defend myself to the ends of the earth.  Anyone who calls me a non-classroom pedagogue deserves to be righted…but then I kept reading…and someone with the alias ‘savedabol’ wrote this:

‘Carmel Schettino (the author) led a seminar I took at the Exeter math conference last summer. She is incredible. I can assure you that she is not a non-classroom pedagogue. She has been in the classroom nonstop for at least 20 years (that I know of). She is particularly scholarly when it comes to PBL and other ed topics, but that doesn’t make her irrelevant to what we do every day. Near the end she gives some great resources.’

I can’t tell you how affirmed I felt by ‘savedabol’ and I want to just let them know how nice that was of them to share their thoughts about my work with them.  I have been in the classroom non-stop since 1990 (except for two terms of maternity leave and one term of a sabbatical when I was a full-time student myself) and I pride myself in researching as much as possible about what I do.

I do wish that the first poster had had the chance to hear me speak instead of jumping to the conclusions they had – and it definitely got me thinking about something that was discussed last year at the PME-NA conference in October 2012.  I was one of maybe just a few people in the special category of math teacher/educator/researcher/doctoral students at this research conference where many of the math research folks were talking about ways in which they could breach the great divide of the theory people (them) and the practice people (us).

For many years I have lived this double life of both theory and practice and I have to say, I love it.  Having just finished up my Ph.D. and teaching full time was probably one of the toughest things I’ve had to do in my life, but having my mind constantly in both arenas has only helped me be a better teacher and a better researcher.

Jo Boaler is a great researcher at Stanford University who is doing great work in outreach between theory and practice this summer by offering a free online course called “How to Learn Math.”  It’s a course for k-12 teachers that is grounded in the most recent research in math education.  What a great idea!  She is sharing some of her wisdom freely online with k-12 teachers who want to spend some time learning about new ideas themselves.  I know I’m in.

In August 2008, the NCTM put together a special Research Agenda Project to work on recommendations for just this cause and you can see their report here.  One of the major recommendations that came out of their work was to not only emphasize the need for communication between researchers and practitioners, but in my view to help them realize that this communication would benefit both parties equally.  We all have something to share with each other and I know that I appreciate every classroom practitioners’ experiences.  I learn something from every teacher that ends up in my workshop every summer and often end up using many of their ideas as they do mine.

So let’s keep supporting each other both in real life and virtually, and realize that often times, the “bleeding obvious” is something that needs to be stated and discussed over and over again to be sure that we are still talking about it with the right people.