Returning from vacation is always a tough time, but the other day in my honors geometry class, I decided to present them with a problem that had at its heart the Pythagorean Theorem – which we’ve been using since the beginning of the year – and I wanted to see what they would do with it.  So I showed them this video I found on line.  It poses an interesting question regarding buying android tablets and what size you might want.  Before we watched it, I had them search online to compare the prices of some well-known tablet brands and see if there was a major difference in their 7 inch size tablet vs. their 10 inch size tablet.  We came up with some prices that looked like this:

We talked about how, in most cases the price of the 10 inch tablet was about 1.5 or 1.6 times the price of the 7 inch tablet.  Was that reasonable?  Did it make sense?  10:7 was only about 1.4.  So then we watched the video:

Visit NBCNews.com for breaking news, world news, and news about the economy

I posed the question to them, “Do you think what this guy is saying is true?  Is the 10 inch table really twice as big as the 7 inch? If so, what evidence can you give to say that it is and how can we justify whether or not any of these tablets really are?”

Great conversation ensued.  I was so excited.  One group of students started trying to find numbers that the dimensions of the two tablets could be.  Of course, the first thing they assumed was that the one with the 10-inch diagonal screen would have width of 6 and height of 8 (don’t we all just love those Pythagorean Triples?) but then they realized when they did that there could be so many other triangles that could have a hypotenuse that was 10 as well.

Another group started trying to compare the areas of the screens to see if they could find dimensions of two tablets that actually had one area that was twice as big as the other one (that kept the diagonals 7 and 10).  This was an interesting group because they had thought through the concept of “twice as big” but hadn’t made the jump to what it would mean for one to be that much bigger.

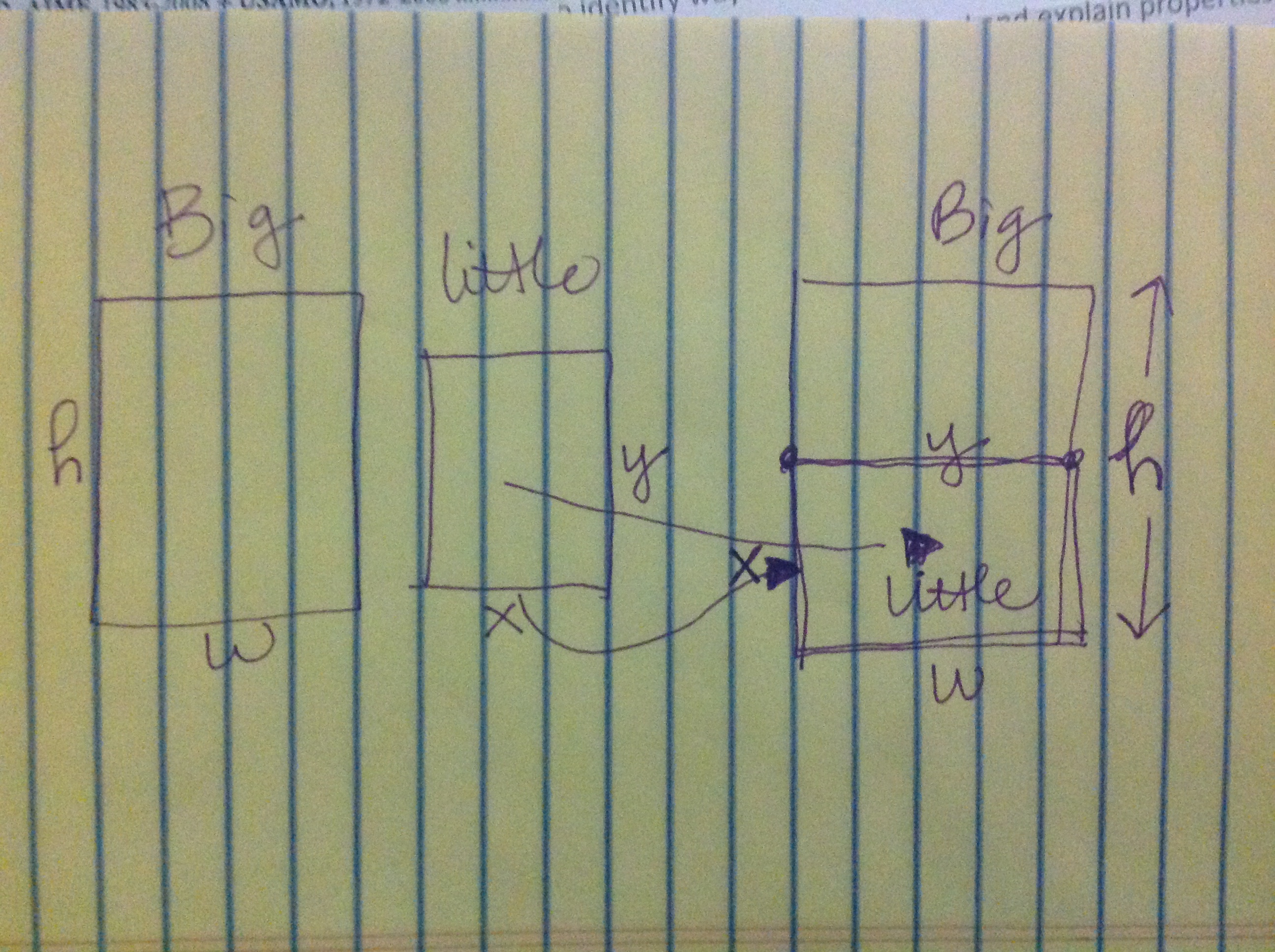
I was then called over to a group where a girl was trying to explain her idea of how to make two 7 inch tablets fit into the 10 inch tablet.  I’ll call her Tracy.  Tracy said something like this to me: “If ttwo small ones fit into one of the big one, that would mean that the height of the big one is twice as big as the width of the little one” and she proceeded to go up to the board and draw a picture like this:

This started everyone talking.  It actually became really cool for a while.  They soon realized that you could let the dimensions of the smaller tablet be w and 1/2h while the dimensions of the bigger one were h and w.  This combined with the Pythagorean Theorem allowed them to solve a quadratic system of equations to find the dimensions of both tablets, if it were true that the 10 inch tablet were truly “twice as big” as the 7 inch. (I believe the 10 inch tablet had to be 8.24 inches by 5.65 inches approx).

We were unable to confirm all of this by finding dimensions online so if anyone can do this, please let me know!  But what was the most amazing part of this problem solving exercise for me and my students was the engagement that I observed from their interest in the problem and their own motivation to come up with a way to justify or debunk the claim made in the video.  We are going to write up some paragraphs about their findings and present them to each other next time we meet.

I was very proud of the way they were not afraid to experiment with different ideas initially and how Tracy moved through her own ideas and took risks with the group and those around her, eventually getting her and others to the path that made sense to many of them.  It was really a group effort and worked well.  If anyone else tries this, please let me know how it goes.