Category: Uncategorized

Sharing in Chicago! PME-NA 2013

So tomorrow I’m off to PME-NA 2013 in Chicago which is one of my most favorite conferences for mathematics education research.  I will be presenting my research findings from my dissertation on Saturday morning and I’m so lucky to be going.  I’ve posted my PMENA handout  for anyone interested in having it.  I’m also posting  the powerpoint on my slideshare site.

Buyer Beware…when using rubrics for critical thinking skills

One of my goals in my work is often to help classroom mathematics teachers to be more deliberate in the ways in which they assess problem solving.  Although many people can be cynical about rubrics, I think that students can find them at least helpful to know what a teacher expects of them.  I have some students who told me that they pull out my rubric for grading journal writing almost every time they go to write a journal entry this fall.

However, a rubric that is vague and ambiguous about expectations can cause more harm than good.  Just throwing a rubric around that students can look at, or one that you can post on your website that you can show an administrator and say, “See, I have a rubric for that” isn’t necessarily a good thing.  Especially for problem solving.  Problem solving as a process is a very difficult thing to nail down for students especially in terms of the levels of how they can improve in their work.

I recently ran across this rubric that posted on a website under the title “Awesome Problem Solving Rubric for Teachers.”

Is this an “Awesome Rubric” for teachers?

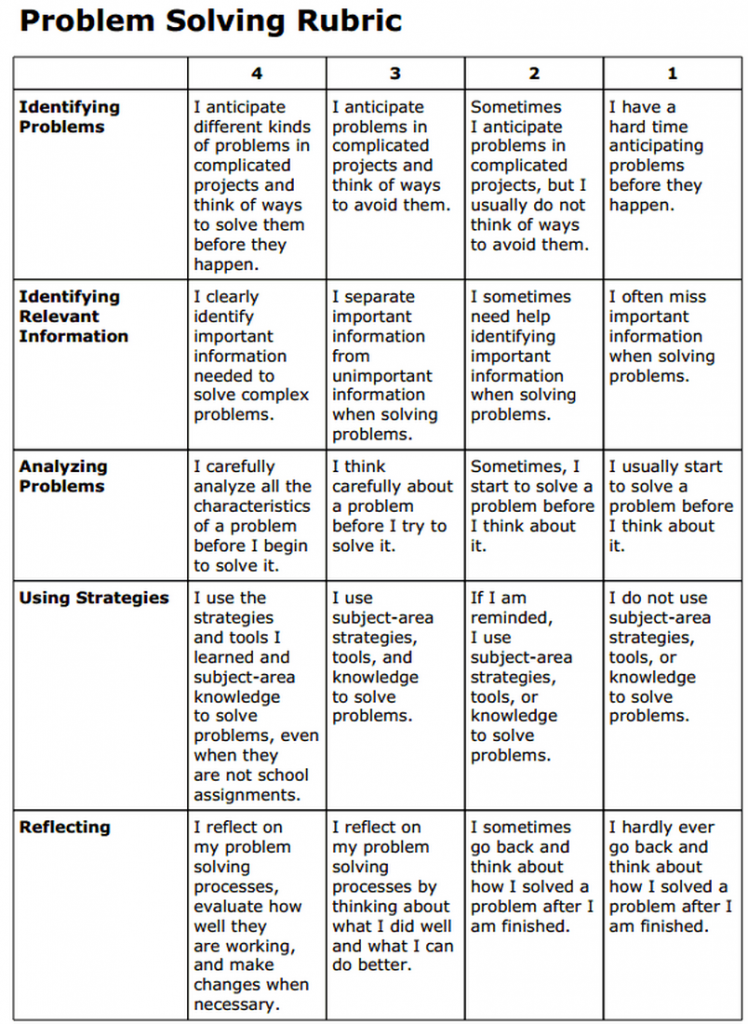
As I read through this, at first glance the categories look pretty good – Identify the problem, identify relevant information, analyze the problem, use strategies and reflect on the process.  Sounds like a pretty standard problem solving process –very similar in many ways to Polya’s process or the steps that Jo Boaler discussed in her online course How to Learn Math this summer.

The graded level descriptors of how a student might be able to see where their work “fits” in the rubric seems to only put the behaviors on a “continuum” of Always- sometimes- never instead of trying to describe actions that the student could do that describe a mediocre way of using a strategy.    For example, analyzing a problem can be so much more descriptive than just “I think carefully” about the problem before a student starts.

They could:

1. listen deliberately to others’ ideas and reflect on them in writing or verbally

2. question the given information of a problem – does it make sense in a realistic way?

3. think about the representations they can come up with for the problem – does a graphical approach make the most sense?  Why?  Would making a geometric representation be better, if so why?

4.  In comparing a new problem to ones I’ve already done, can I list the similarities and differences?  What is this question asking that others I’ve done not asked?

How many students can really ascertain what “thinking carefully” about a problem is?  I have found that more and more we need to erase as much ambiguity as possible to help students learn to be critical thinkers.  As we feel the need to teach critical thinking, reasoning skills and sense making, it is even more imperative to have rubrics that are as precise as possible.

Now, I don’t claim that mine are perfect, but my rubrics and student feedback forms have gotten some pretty good reviews from teachers and successful feedback from students.  I work on them every summer and am continually editing in order to be more deliberate about the feedback I give my students.

I also highly recommend the rubrics from the Buck Institute Website under their “tools” category.  I also adapted one of their critical thinking rubrics that was aligned to the Common Core and changed it directly for my PBL curriculum – more for presentation of problems and novel problem solving.  I’m still working on it because I have to think about exemplars for what would be above standards, but let me know if you have any feedback.

Critical Thinking rubric for PBL

So, I would just warn anyone to beware of “awesome rubrics” for teachers that they find on the internet because something that might seem awesome at first glance might end up doing more harm than good.

Minimizing Shame in the PBL Classroom…and maybe Daring Greatly?

I recently read a blogpost by one of my favorite authors, Brene Brown, of TED talk fame, and the author of a great book about vulnerability called Daring Greatly.  In her blogpost Brene wrote about some reactions to a comment she made on Oprah Winfrey’s Super Soul Sunday show where she talked about shame in schools about which she received a great deal of criticism in the blogosphere and on twitter.

I kept reading as I was shocked that anyone would be offended by anything that Brene Brown could say – especially teachers.  She has always been extremely inspiring and very supportive of teachers – as a teacher herself, her book, Daring Greatly, has a whole chapter on how schools can support a community to come together around vulnerability and become closer and foster creativity and innovation in this way.

However, she talks about the research that she has done about learning and teaching.  She says,

“As a researcher, I do believe that shame is present in every school and in every classroom. As long as people are hardwired for connection, the fear of disconnection (aka shame) will always be a reality. ..Based on my work, I do believe that shame is still one of the most popular classroom management tools.”

Think about it.  When you talk to adults about their memories of school, and specifically math classrooms, many people will tell stories of being embarrassed or humiliated about getting something wrong, about feeling less than adequate or unworthy of being in the class they were in.  Even if the teacher was not doing anything deliberate, if a student has the courage to answer a teacher initiated question and get it wrong, the response that is given can make or break their self-worth that day.

I’ve been giving this a lot of thought in the context of the PBL Classroom – How are we supposed to be teaching students how to take risks and not be afraid to be wrong and make mistakes in their learning if they have this fear of shame that is so deeply entrenched in our culture?  Especially in mathematics classrooms, how are we supposed to undo so many negative experiences that may have affected a student’s ability to allow themselves to be vulnerable and learn in this way?

PBL relies on the fact that a student is willing and able to make connections and conjecture regularly – numerous times in a class and on their own during “homework” time.  Being wrong and uncertain is really the norm and not the anomaly in this classroom.  As October rolls around and I hear more from students (and parents) about the discomfort they are feeling, I really do understand how different this is for everyone.  However, I do think we need to rely on the fact that students can be resilient and strong when pushed to try new things and to learn in a way that is good for them.  It is just that resilience that will make them better leaders, learners and more creative in the work force later on in life.

In talking to some students recently, I asked them where they thought they would learn more, in a classroom where it was laid out for them what they had to do or where they had to make choices about methods and sometimes it would be unclear.  I could tell that one girl was really struggling with that question.  She knew that it would be easier in the other classroom, but also knew that she would learn more and wanted to stay where her learning would be more effective.

What can I do to help this process go more smoothly?  Make sure that they know that I am working hard NOT to use shame as a classroom management tool.  That I am sincerely interested in the mistakes that they are making and how it is helping their learning.  I want them to grow from their errors and misconceptions and find ways to use those to their advantage.  I want to add to their self-worth not only as a math student, but as a problem solver in every way.

As Brene Brown says:

“I don’t believe shame-free exists but I do believe shame-resilience exists and that there are teachers creating worthiness-validating, daring classrooms every single today.”

I can be truly aware of the language that I use and the questions that I ask in order to make sure that everyone’s voice is heard and that my students know that I want to hear their ideas.  It’s really the only way to get them to Dare Greatly!

PS – Check out the wonderful quote by Teddy Roosevelt that I use in my PBL classes about Daring Greatly that Brene Brown used for the title of her book.

Anja S. Greer Conference 2013

What a great time we had this week in my courses!  I am so excited by all of the folks that I met and the CwiC sessions of other leaders that I went to.  Pretty awesome stuff presented by Maria Hernandez from NCSSM, my great colleague Nils Ahbel, Tom Reardon, Ian Winokur, Dan Teague, Ken Collins and many others.  I was so busy that I didn’t get to see many other people’s sessions so I feel somewhat “out of it” unfortunately.

I want to thank everyone that came to my CwiC’s and remind them to be sure to go and pick up my materials on the server before they leave.

For my participants – here are the links to the course evaluations:

Moving Forward with PBL: Course Evaluation

Scaffolding and Developing a PBL Course:  Course Evaluation

Defying Gravity as a Means to Learning from Mistakes

There’s a lot of blogging, writing and research (and anecdotal stories) out there these days about trying to foster the value in students for the appreciation in failing.   I even wrote a blog entry two years ago entitled “modeling proper mistake-making” way before I read anything or watched any videos on the Internet.  From teaching with PBL for over 17 years, I am a pro at making mistakes and watching students struggle with the concept of accepting the idea of learning from their mistakes.  This is so much easier said than done, but it is clearly something that grow to love even if only for a short time.

Last April, I had the pleasure of hearing Ed Burger at the NCTM national conference where he spoke about having students in his college-level classes required to fail before they could earn an A in his class.  In his August 2012 essay “Teaching to Fail” from Inside Higher Ed (posted at 3:00 am, which I thought was kind of funny), he talks about attempting to make a rubric for the “quality of failure” on how well a student had failed at a task.  I thought this was an interesting concept.  I mean, in order to fail well, can’t you just really screw up, like not do it at all?  Prof. Burger states that allowing students to freely reflect on their “false starts and fruitful iterations” as well as how their understanding “evolved through the failures” can be extremely beneficial.  He also states:

“To my skeptical colleagues who wonder if this grading scheme can be exploited as a loophole to reward unprepared students, I remind them that we should not create policies in the academy that police students, instead we should create policies that add pedagogical value and create educational opportunity.”

Last year for the first time, I tried a similar experiment wherein I gave students an assignment to write a paper in my honors geometry class.  They had to choose from three theorems that we were not going to prove in class.  However, it was clear that they could obviously just look up the proof on the Internet or in a textbook or somewhere, since they clearly have been proven before.  The proof was only 10 or 20% of their grade.  The majority of the paper’s grade was writing up the trials and failures in writing the proof themselves.  This proved to be one of the most exciting projects of the year and the students ate it up.  I even told them that I didn’t care if they looked up the proof as long as they cited it, but I still had kids coming to me to show my how they were failing because they wanted a hint in order to figure it out themselves.  It was amazing.

This past week I showed my classes Kathryn Schultz’ TED talk entitled “On Being Wrong” in which she talked about the ever popular dilemma of the Coyote who chases the Road Runner, usually off a cliff.

My students loved her analogy of the “feeling of being wrong” to when the Coyote runs off the cliff and then looks down and of course, has to fall in order to be in agreement with the laws of gravity.  However, I proposed a different imaginary circumstance.  Wouldn’t it be great if we could run off the cliff, i.e. take that risk, and before looking down and realizing that vulnerability and scariness, just run right back on and do something else?  No falling, no one gets hurt, no one looks stupid because you get flattened when you hit the ground?  Maybe that’s not the “feeling of being wrong” but it’s the “feeling of learning.”

Next blog entry on creating the classroom culture for “defying gravity.”

Some (hopefully) helpful Mobile Technology (i.e. iPad) information

This past week I spoke with many teachers who are being asked to implement an iPad program in their schools this coming year and feel as though they are lost in the woods. Although their schools are doing what they can to support math teachers in their endeavors, the truth is that the “mobile technology of the future” (i.e. the direction that most technology coordinators say that education is moving) really has not caught up with the needs of mathematics educators. In a presentation I gave last week, I made the distinction between three different types of apps that exist out there for math teachers to use. I believe that the “tool apps” are useful when you want the mobile device to replace an actual tool or a skill that students have learned or that you feel can be replaced but a short cut. Great examples of these are ruler or protractor apps. However, beware of apps that are tools for doing the quadratic formula – just pop in a, b, and c and 30 “practice” problems can be done in 5 minutes (although I could go off on having students do 30 of the same type of problem for homework too). These apps are not necessarily made to aid in the process of learning for students.

Secondly, there are the “review apps” – the ones that are created to help students prepare for standardized tests, name all the theorems in geometry from A to Z, list all the possible types of polygons and their interior angles, etc. These are helpful apps for reference once a student has learned the material and for reviewing for end of year exams, etc. However, once again they do not necessarily aid in the learning of the material.

The third kind of app is what I was truly looking for – these “teaching apps” are really “understanding apps.” They make the process of understanding a concept or whatever is going on in the classroom more productive, efficient, interesting or engaging. I have to say that sadly, these apps are far and few between. I have surfed many a math app blog on the internet and there is no distinction between these three categories and in my mind, teachers want a distinction. Many of the ratings in the iTunes store are made by students so I recommend reading the review and if it says something like “This app is great. It let me do my homework in 5 minutes” (5 stars), my guess is it’s not necessarily the app you are looking for. Here is the list of apps I gave out at my CwiC session that I found useful and within this third categories of math education apps.

The last thing I had to comment on was the fact that the iPad (and mobile devices in general) have a way to go before they catch up with the old Tablet PC when it comes to digital ink. Writing, for a mathematics teacher, is still the easiest way to put equations into lesson plans, tests, board presentations, problems, correcting papers, etc. So although we are not artists looking for the best stylus for drawing or sketching, we actually do drawing and sketching. We are not business-people who take notes during hugely important meeting with clients, but it still is annoying when your stylus makes noise on the glass screen in a meeting with administrators or even in class with students. And having a wrist guard or palm protector that actually works (and doesn’t make the screen move or leave marks) in the note-taking app, is extremely important to us. We also need drawing tools like geometry shapes, coordinate axes, and hopefully (dare I ask) access to symbolic text, like Greek letters.

At the conference I got into a great conversation with some teachers about different styli and which were the best. I found a Great Stylus Video Review online that I highly recommend if you are looking for a new stylus for your mobile device for writing or doing mathematics. I think I might actually order the Maglus from overseas to see how good it is.

Keep in touch about the mobile apps you are using, cause I’d love to hear about them. I do believe that someday the devices and their technology will catch up with the needs of math teachers, but for now, I sort of miss my Tablet PC and OneNote for writing – 🙁 But I am loving playing with all these new apps. I’m like a kid in a candy store, but hopefully more productive.

Problem-Based Assessment?

This time of year always has me and my colleagues thinking about the way we cumulatively assess our students in the PBL courses. Since cooperation and problem solving are so important to us we are committed to having some type of collaborative experience as part of the final “exam” but we also have a committment to assessing the content knowledge as well. It’s a difficult thing to balance though, as many of you know. However, since we have come to the decision that this course is really about depth and not breadth, we do not believe that the main focus should be on testing memorization of fact or to see if they can do “one of every problem” that we covered this year.

We have split our two hour final “exam” into a group problem solving experience from which the students receive part of their exam grade (and they turn in one paper as a group). The rest of the exam grade comes from an individual 40-minute performance they do on their own. In general, the grades come out very much as we expect for individual students. During the group problem solving part (approximately one hour and 20 minutes), the teachers walk around and observe the interactions in the groups – who’s leading, who’s following, who’s just sitting back and others do the work. This factors into their grade. We also allow students to give feedback into how the group worked together and for alternative answers if they require it.

If anyone has questions about the way we write questions or would like to talk about assesment in PBL, please post some questions in the Forum about it. Looking forward to doing some more work about assessment in my course at the PEA conference this summer.