Category: Uncategorized

How do you justify the time that PBL takes?

4 Comments

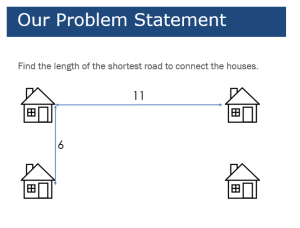
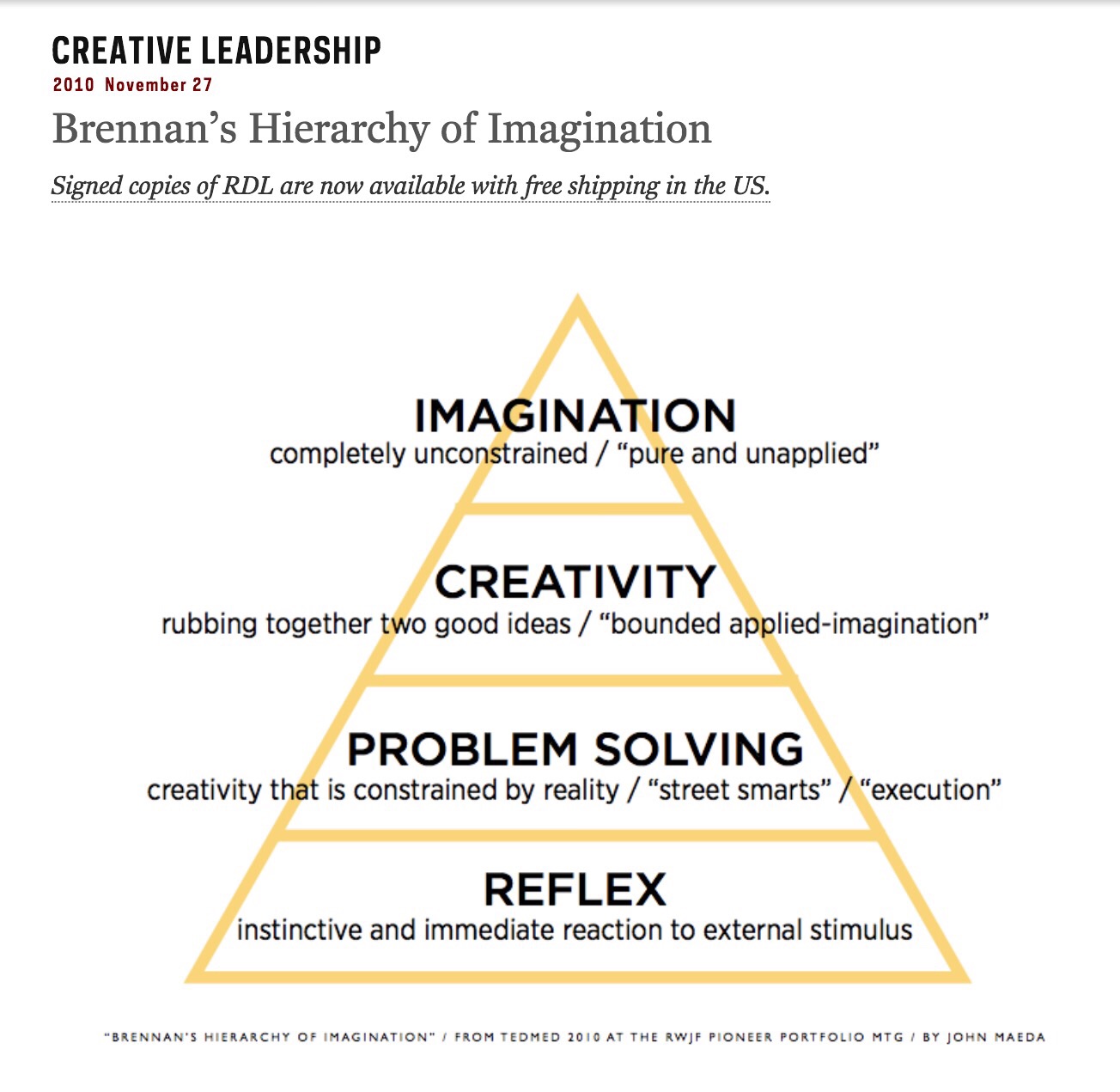
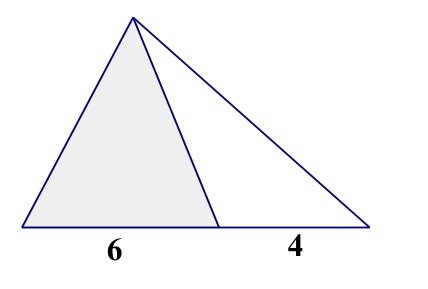
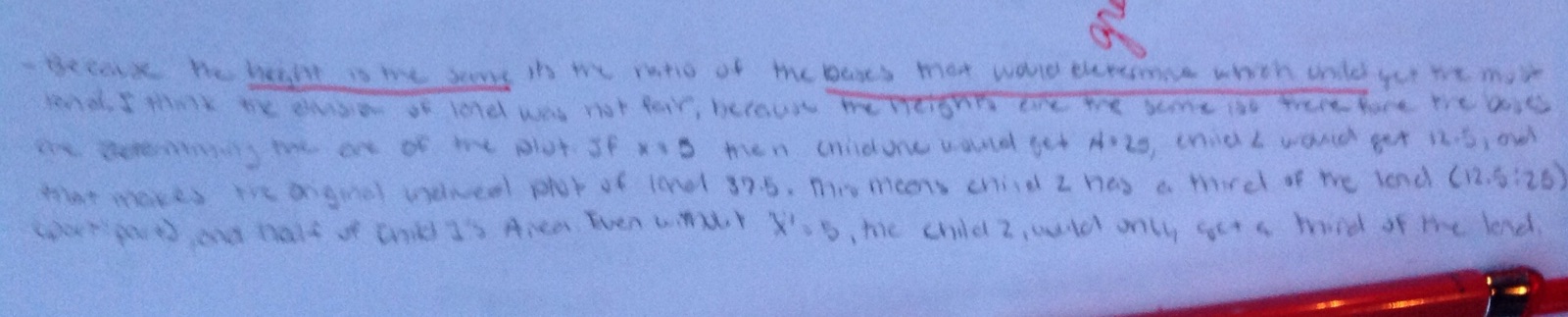I just wanted to respond to a really great question that someone asked on Twitter the other day.

This is a common concern of teachers starting out with the idea of PBL. What does “Class Discussion” mean, first of all? I would agree that discussion does “eat up valuable” time in class on a daily basis, for sure. But what is actually happening in that discussion where something else would be normally happening in the math classroom? What does the discussion replace?

In my mind the discussion itself replaces the lecture, teachers ‘doing of problems” for the kids to then repeat, then kids often sitting on their own or in pairs doing problems that were just like the ones the teacher showed them how to do. The importance of the class discussion (which honestly is the main idea of PBL) is for students to share their ideas of prior knowledge, connections between problems, where they are confused and see where others were not confused and what prior knowledge and experience they brought to the problem.

Here’s a diagram that I use when doing PD work with PBL teachers to help explain all of what is supposed to be happening during class (it’s a lot!)


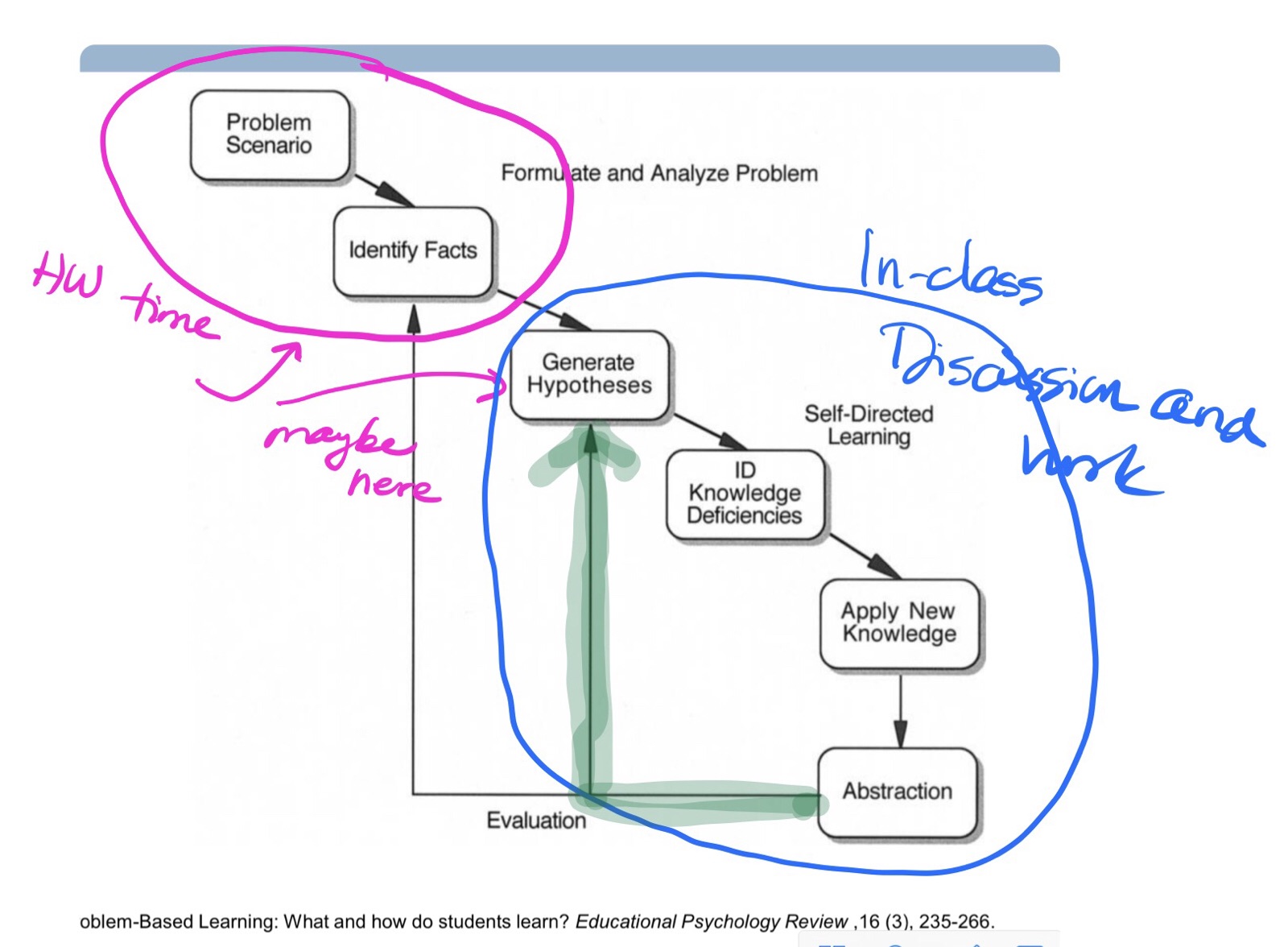
The student presentations are really just a jumping-off point. It is not just for students to explain “how they did a problem” – as they say – or they think what they’re supposed to do. The steps of Hmelo-Silver’s “process of learning in PBL” diagram that I’ve circled in pink is what students would/should do for homework. However, the part that is circled in blue is actually the learning process that happens in the class discussion – so is this time that has been “eaten up” in class or is it actually a very necessary part of the important learning, reflection and self-regulation of the process that needs to happen?

Is this harder for students? Heck, Yeah. There is so much more focus, listening, questioning and reflection that is needed in order for this process to be successful and productive. But there are ways to make it easier for students and that’s what the “class discussion” time is for. It takes a lot of practice and mastery on the teachers’ part to realize what is needed. Making mathematics discussion productive is a very important part of teaching in PBL and definitely not a part that should be seen as subtle, intuitive or straightforward.  There is so much more to this that I can not put in a single blog entry, but it’s definitely worth beginning the discussion.  Would love to hear others’ thoughts.

Modeling with Soap Bubbles

2 Comments

I am so very lucky to have a guest teacher with me this year at my school.  Maria Hernandez (from the North Carolina School of Science and Math) is probably one of the most energetic and knowledgeable teachers, speakers and mathematicians you could ever find – and we got her for the whole year!  We are so excited.  I am working with her and she is so much fun to work with.  I have been teaching calculus with PBL for almost 20 years now and thought I had all the fun I could but no!  Maria is bringing modeling into my curriculum and I’m enjoying every minute of it.

As we started teaching optimization this week, Maria had this wonderful idea that she had done before where we want to find the shortest path that connects four houses.

picture-of-houses

I let the kids play with this for about 10 minutes and then did this wonderful demonstration with some liquid soap bubbles and glycerin.  We had two pieces of plastic and four screws that represented the houses.  As the kids watched, I dipped the plastic frame into the liquid and voila-file_000

Right away the students saw what they were looking for in the shortest path.  Now they had to come up with the function and do some calculus. As they talked and worked in groups, It was clear that using a variable or one that would help them create the right function was not as easy as they thought.  However,  I was requiring them to write up what they were doing and find a solution so they were working hard.

file_000-1

We have been doing a lot of writing in Calculus this fall so far and they are getting used to being deliberate about their words and articulating their ideas in mathematical ways.

Here is the outline of the work they did in class: Shortest Path Lab

and here is the rubric that I will be using to grade it.

rubric-for-lab-3-2

The engagement of students and the buzz of the classroom was enough to let me know that this type of problem was interesting enough to them – more than the traditional “fold up the sides of the box.”  The experience they had in conjecturing, viewing, writing the algebra and solving with calculus was a true modeling experience.

If you decide to do this problem or have done something like it before, please share – I’d love to do more like this.  I am very lucky to have a live-in PD person with me this year and am grateful every day for Maria!

 

Being Imaginative in Problem Solving

2 Comments

Sometimes my ignorance with respect to Twitter just floors me. Today alone I made two huge faux pas (is that plural?) with two people that I really respect and just made a fool out of myself – typos, misinterpretations, and misunderstandings abound in my tweets. But I have to say I press on – because I have found so much that informs my teaching and learning that I can handle the fool-making and embarrassment.

So here’s one thing that I did a few weeks ago – someone tweeted about this great article that I, of course, then went and read, took a picture of the great diagram in the article – but forgot to “like” or “favorite” or whatever it’s called now. So now I can’t give credit to whomever brought me to this wonderful enlightenment about which I will now write. So if you are reading, sir/madam, who tweeted this article, please forgive me.

I read this short blogpost entitled “Brennan’s Hierarchy of Imagination” and immediately made the connection to PBL.


The author, John Maeda, wrote about a conversation he had with Patti Brennan about Maslow’s famous Hierarchy of Needs of students in their learning. These two were talking about the fact that teaching creativity is really hard and Patti Brennan was thinking that it was a bit easier to teach someone to use their imagination. She was talking about this in the context of the health care field – trying to help people empower themselves to help themselves.

Of course, the first thing I thought of when I saw this pyramid was problem solving. I thought this was brilliant! The foundational, lower level of reflex or instinct is analogous to doing problems that you have seen before. Students love this instinct – the idea that if you can do a problem that someone has shown you how to do, that you are problem solving, – it gives them a reaction of completing something, some kind of satisfaction.

The next level which is appropriately called problem-solving is when you are actually solving a problem that has occurred but is constrained and you are executing skills. I love this. It still takes some talent and analysis, but you are still just reacting to a given situation. Perhaps putting together two different methods that someone showed you and seeing what happens?

The third level that she calls creativity is the first step to unique ideas and methods. The first attempt at doing something in a different way – saying what if we tried this? Has anyone every done this before? Why not? It’s still bound by the reality that we experience, but seeks to move past the knowledge that we have.

And finally imagination is what I think happens when my 4-year-old niece explains how the clouds got up in the sky because the stars moved so fast pieces came off and clumped together, or when a student can’t figure out if there are more real numbers between 0 and 1 as there are integers and they try to describe the size of those sets to me with things they imagine.

If I’m lucky, I’d say some of the kids in my classes get to creativity – in fact I think that’s been my goal as of late. To get them at least to experience it with some projects, assignments and good problems. To get them to realize that mathematics is more than just a reflex or even just reiterating a process.

Hopefully, this coming year the number of kids who will get to that third level will increase, but who knows? I do love this framework because at least I know I don’t want them stuck on that bottom level for level for long.

Documents for CwiC Sessions at Anja Greer MST Conference 2016

Instead of passing out photocopies, I tried to think of a way that participants could access the “hand-outs” virtually while attending a session.  What I’ve done in the past a conferences is have them just access them on their tablet devices.  You can also go and access copies on the Conference Server if you do not have a device with you (you should be able to use your phone too).

These link to This is an Adobe Acrobat Documentpdf documents that I will refer to in the presentation about “Assessment in PBL”

Information on Spring Term Project and Spring Term Project Varignon 2015 (this document includes rubric)
Keeping a Journal for Math Class
Revised Problem Set Grading Rubric new
Rubric for Sliceform project and Sliceforms Information Packet
Weekly-Learning-Reflection-Sheet

Page at my website with Rubrics and other guides for Assessment

Adventures in Feedback Assessment

On an assessment students did for me today I gave this question:

An aging father left a triangular plot of land to his two children. When the children saw how the land was to be divided in two parts (Triangle ADC and Triangle BDC), one child felt that the division of the land was not fair, while the other was fine with it. What do you think and why? Support your justification with mathematical evidence.

 So this student had a hard time with this question. Since there was no height given and the bases were different, she was unable to think about how to compare the areas. She was however able to say that it would be a fair split if the areas were the same. So since I am doing this work this year with giving feedback first and then grades (see past blogpost “Why teachers don’t give feedback before grades and why they should”) I wrote this feedback on the problem set: 
 I am trying to get her to remember a problem we did in class where there was a similar problem we did with an acute triangle and obtuse triangle that shared the same height:

The area of the shaded triangle is 15. Find the area of the unshaded triangle.

This idea of where the height of obtuse triangles are is a really tough one for some geometry students. But more than that the idea of sharing a height and what effect that has on the area is also difficult.

We will see tomorrow if this student is able to take my feedback and see what whether the division of the land is fair.

By the way, here’s a response that another student had:


Just in case you can’t read it:

“Because the height is the same, it’s the ratio of the bases that would determine which child would get the most land. I think the division of land was not fair, because the heights are the same so therefore the bases are determining the area of the plot. If x=5 then child one would get A=20, child 2 would get 12.5 and that makes the original plot of land 37.5. This means child 2 has a third of the land (12.5:25) (part:part) and half of child 1’s) Even without x=5, the child 2 would only get a third of the land.”

We’ll see what happens!

Virtual Hand-outs for #GlobalMathDept conference

So tonight I give my very first online talk – I’m a little worried that talking to my computer will be a little strange at 9:00 at night, but we’ll see what happens.  Hopefully, there will be some type of audience interaction.  I’m such a relational person that I think I’m one of those people that really needs feedback will I’m talking.  We’ll see!

My hope is to discuss the differences between PBL & PjBL and how people can find a way to make some type of PBL work in their classroom no matter what place they are at in their teaching.

Here are the documents that I will be mostly referencing.  Hope to see you all there!

Student Self-Report on Class Contribution
Thinking_About_Thinking_Problem_Solving_Tool
Weekly Learning Reflection Sheet
Keeping a Journal for Math Class

One of the Original “Makers”

Apologies to any faithful readers out there – I have had a heck of a summer – way too much going on.  Usually during the summer, I keep up with my blog much more because I am doing such interesting readings and teaching conferences, etc. (although I’m running a conference for the first time in my life!) However, this summer I was dealing with one of my biggest losses – the passing of my father after his 8 year battle with breast cancer.  I thought I would honor him by writing a post talking about a problem that I wrote a few years ago, well actually a series of problems that utilized his work when teachers of algebra I asked me how I taught the concept of slope.  So dad, this one’s for you.

In 1986, my dad, Francesco (Frank) Schettino, was asked to work on the renovations for the centennial project for the Statue of Liberty.  He was a structural steel detailer (also known as a draftsman) but he was really good at his job.  Everywhere we went with my dad when I was younger, he would stop and comment about the way buildings were built or if the structure of some stairs, windows or door frames was out of wack.  He could tell you if something was going to fall down in 10 years, just by looking at it.  At his wake last week, one of the project managers from a steel construction company that he worked on jobs for told me that they would save the interesting, most challenging jobs for him because they knew he would love it and do it right.
photo (1)I remember sitting with my dad at his huge drafting desk and seeing the drawings of the spiral stairs in the Statue of Liberty.  He talked to me about the trigonometry and the geometry of the circles that were necessary for the widths that were regulated for the number of people that they needed to walk up and down the stairs.  This all blew my mind at the time – that he needed to consider all of this.  So to be able to write problems that introduce slope to students about this was just a bit simpler to me.

If you take a look at my motivational problems on slope and equations of lines I believe it’s numbers 2 and 3 that refer to his work (excuse the small typo).  Over the years I’ve meant to go back and edit these a number of times.  If you are someone who has taken my course at the Anja S. Greer Math, Science and Technology Conference at Exeter, you are probably familiar with this series of questions because we have discussed these at length and talked about how students have reacted to them (and how different adult teacher-students have as well).  We have assumed no prior knowledge of slope (especially the formula) or the terminology at all.

Some questions that have come up: (with both students and the teacher-students I’ve worked with)

1. What does a graphical representation of “stairs” mean to students?
2. What does “steeper” mean and what causes stairs to be steep?
3.  Why are we given the “average” horizontal run for the spiral stairs? Would another measurement be better?
4. Why does the problem ask for the rise/run ratios?  Is there a better way to measure steepness?
5. (from a teacher perspective) why introduce the term “slope” in #3? can we just keep calling it steepness?

These are such rich and interesting questions. The questions of scaffolding terminology and when and how to introduce concepts are always the most difficult.  Those we grapple with specifically for our own students.  I always err on the side of allowing them to keep calling it steepness as long as they want, but as soon as we need to start generalizing to the abstract idea of the equation of the line or coming up with how to calculate that “steepness” a common language of mathematics will be necessary.  This is also where I take a lesson from my dad in terms of my teaching.  His great parenting style was to listen to me and my sisters and see where we were at – how much did we know about a certain situation and how we were going to handle it.  If he felt like we knew what we were doing, he might wait and see how it turned out instead of jumping in and giving advice.  However, if he was really worried about what was going to happen, he wouldn’t hesitate to say something like “Well, I don’t know…”  His subtle concern but growing wisdom always let us know that there was something wrong in our logic but that he also trusted us to think things through – but we knew that he was always there to support and guide.  There’s definitely been a bit of his influence in my career and maybe now in yours too.

TeachThought Blogging Challenge Day1: Goals for this Year

 OK, so I’ve decided to try to blog more this coming year (like I don’t have anything else to do working at a boarding school) and I happened to run across the TeachThought Blogging Challenge the other day, so I thought I would try to see how many of the 30 days, I might be able to actually write something that was worthwhile.
 
 I even downloaded a new app for my iPad to make blogging easier (we’ll see if that prediction comes true or not) called BlogPress which had some really nice reviews. (Using it right now, with a little help from my java programming husband).
 
 So Day 1 assignment is to “Write your goals for the school year. Be as specific or abstract as you’d like to be.” This is quite an overwhelming task honestly, there are often so many of them. So after some thought I came up with three and here they are:
 
 1. I am mentoring a teaching fellow in my department this year and so one of my goals this year is to be a good mentor. I know that’s pretty abstract but when you have another teacher’s success or failure connected to how well you discuss teaching, mathematics and learning with that person I find the overall goal pretty important. Mentoring someone in PBL is even trickier if it’s their first time teaching and they haven’t actually seen it in action yet. From doing this in the past, I know I also have to find ways to allow young teachers to express their hesitation and doubts with this method of teaching, so being aware of the discussion and keeping the dialogue open will parts of being a good mentor.
 
 2. My second goal is to work on assessing student learning through listening. One of the biggest issues I am grappling with in the classroom and have thought about a great deal in PBL, is how well students can learn from each other by listening to discussion. In fact, I know that one of the biggest arguments that “doubters” have with PBL is that if students are not just told what the important facts are and given clear instruction (what to learn when) learning can’t happen. I want to find ways in which to assess how well students are learning through dialogue. This was inspired when I heard a talk a year or so ago by Karl Kosko (Kent State University) about a study he did related to student listening and their learning. If I remember correctly there was a direct relationship between how well a student could articulate their ideas during a conversation and how well they listened. (So talking and listening are connected.)
 
 3. My third goal is to think about the connections between PBL and grit or self-efficacy. I gave a lot of thought this summer to the differences between grit and self-efficacy and I think one of the best differences I found was tweeted by a guy named Duane Sharrock (@DuaneSharrock) when he responded to request for any distinctions that people had in a tweet I put out there. He said:
 


So in my mind it seems like Self-Efficacy has more to do with confidence and self-attribution of skills and Grit might have more to do with persistence and determination. I am actually interested in both with respect to what PBL fosters in students. To that end, I am going to do a lot of reading and research to see what’s out there and would love to hear from any readers if you have thoughts or experiences with this.
 
 There are my three main goals for the year. My classes start on Friday, but tomorrow they all arrive – wish me luck! Good luck to all of you out there!

What does “making students metacognitive” mean? – answering “why should someone learn?” in Math

So I recently tweeted a nice article that I read that discussed “12 Questions to Help Students See Themselves as Thinkers” in the classroom (not specifically the math classroom

 

and appropriately, Anna Blinstein tweeted in response:

 

So I thought I needed to respond in a post that spoke to this question. First of all, I should state the caveat that even when I am in a more “standard” classroom (i.e. not a PBL classroom) – which happened to me last year – I try as much as possible to keep my pedagogy consistent with my values of PBL which include

1) valuing student voice
2) connecting the curriculum
3) dissolving the authoritative hierarchy of the classroom
4) creating ownership of the material for students

I find that helping students to be metacognitive helps with all of this. An important aside her is also Muller’s definition of 21st century learning* which is much more than that 20th century learning and education that often comes with direct instruction in the mathematics classroom (not always).I think it’s important to note that the more fluid concept of knowledge that is ubiquitous with technology today and is no longer static in textbooks or delivered by teachers.  Students can go find out how to do anything (procedurally) nowadays, but it is the understanding of it that is more important and the true mathematical learning and sense making.

Anyway, I think I would write way too much if I responded to every one of the questions, but how would I use these questions in my direct instruction class that I taught last year?  What I tried to do was introduce a topic with some problems (and then we would do some practice with problems from the textbook so I could keep up with where my colleague was in the material).  Well, this course was Algebra II, which often referred to prior knowledge that always reminded students of something they had studied before.  I let them use computers to look things up on the internet and use the technology at hand, GeoGebra, Graphing Calculators, each other to ask questions about the functions we were studying.  They could look up topics like domain, range, asymptotes (why would there be an asymptote on a rational function)…but then the bigger questions like “what am I curious about?” had more to do with how did those asymptotes occur, what made vertical vs. horizontal asymptotes and then I would have them do journal entries about them (see my blogposts on metacognitive journaling – journaling and resilience, using journal writing, page on metacognitive journaling).

The more “big picture” questions like “Why learn?” and “What does one *do* with knowledge?” I find easier to deal with because the students ask those.  I think that all teachers find their own ways to deal with them, but I enjoy doing is asking students about a tough question they are dealing with in their life – I use the example of whether or not I should continue working when I had my two kids.  Was keeping my job worth it financially over the cost of daycare? and of course I had to weight my emotional state when I wasn’t working – this is why I enjoy learning and what I do with my knowledge.  When kids see that there’s more to do with functions than just points on a grid, it becomes so much clearer for them – but you know that!

What I really like about Dr. Muller’s list is that he lays out some nice deliberate ways in which we as math teachers can get students to think more clearly and reflectively about mathematics as a purposeful process as opposed to a just procedures that they can learn by just watching a Kahn Academy video.

 

*”Learning – here defined as the overall effect of incrementally acquiring, synthesizing, and applying information – changes beliefs. Awareness leads to thoughts, thoughts lead to emotions, and emotions lead to behavior. Learning, therefore, results in both personal and social change through self-knowledge and healthy interdependence.” Muller http://tutoringtoexcellence.blogspot.com/2014/08/helping-students-see-themselves-as.html