Category: Research

Does PBL teach Resilience?

I just read a great blogpost by a business writer, Gwen Moran, entitled, “SIx Habits of Resilient People.” When I think of people that I admire in my life for their resilience there was usually some circumstance in their life that led them to learn the quality of resilience because they had to. Even the examples that the author uses in this blogpost – being diagnosed with breast cancer, almost being murdered by a mugger, the inability to find a job – these tragedies that people have had to deal with can be turned into positive experiences by seeing them as ways in which we can learn and grow and find strength within ourselves.

But wouldn’t it be great if it didn’t take a negative experience like that to teach us how to be resilient? What if the small things that we did every day slowly taught us resilience instead of one huge experience that we had no choice but to face? Having to deal with small, undesirable circumstances on a daily basis, with the help and support of a caring learning community would be much more preferable, in my opinion, than surviving a mugging. (Not that one is more valuable than the other). But I just wonder – and I’m truly ruminating here, I have no idea – if it is possible to simulate the same type of learning experience on a slower, deeper scale by asking students to learn in a way that they might not like, that might make them uncomfortable, that asks more of them, on a regular basis.

I think you know what I’m getting at. Does PBL actually teach resilience (while also teaching so much more)? In my experience teaching with PBL the feedback I’ve received from students has been overwhelmingly positive in the end. But initially the comments are like this:

“This is so much harder.”
“Why don’t you just tell us what we need to know.”
“I need more practice of the same problems.”
“This type of learning just doesn’t work for me.”

Having students face learning in an uncomfortable atmosphere and face what is hard and unknown is difficult. Thinking for themselves and working together to find answers to problems that they pose as well as their peers pose is very different and unfamiliar. But does it teach the habits that Gwen Moran claim create resilient people? Let’s see. She claims that resilient people….

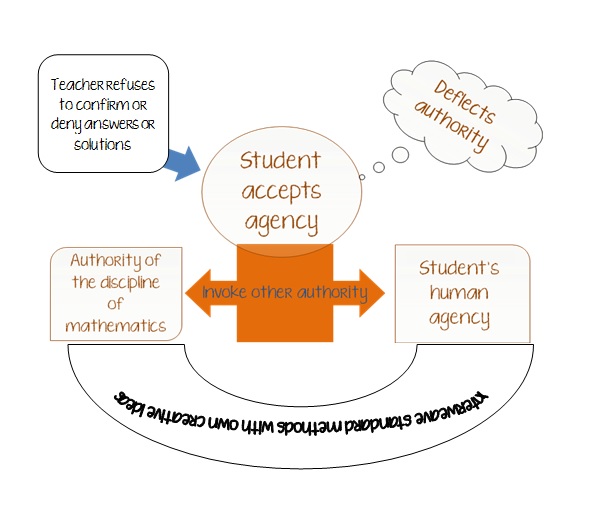
1.Build relationships – I think I can speak to this one with some expertise and say that at least if the PBL classroom is run with a relational pedagogy then it is very true that PBL teaches to build relationship. My dissertation research concluded nothing less. In discussing and sharing your ideas, it is almost impossible not to – you need relational trust and authority in order to share your knowledge with your classmates and teacher and this will only grow the more the system works for each student.

2. Reframe past hurts. – If we assume that real-life “hurts” are analogous to classroom mistakes, then I would say most definitely. PBL teaches you to reframe your mistakes. PBL is a constant cycle of attempting a problem->observing the flaw in your solution ->trying something else and starting all over again. This process of “reframing” the original method is the means by which students learn the the PBL classroom.

3. Accept failure – This may be the #1 thing that PBL teaches. I am constantly telling my students about how great it is to be wrong and make mistakes. You cannot have success without failing in this class. In fact, it is an essential part of learning. However, students in the US have been conditioned not to fail, so that reconditioning takes a very long time and is a difficult process.

4. Have multiple identities – In a traditional classroom, certain students fulfill  certain roles – there’s the class clown, the teacher’s pet, the “Hermione Grainger” who is constantly answering the teacher’s questions, etc. But what I’ve found happens in the PBL classroom is that even the student who finds him/herself always answering questions, will also find him/herself learning something from the person s/he thought didn’t know anything the next day. Those roles get broken down because the authority that once belonged only to certain people in the room has been dissolved and the assumption is that all voices have authority. All ideas are heard and discussed. PBL definitely teaches a student to have multiple identities while also teaching them a lot about themselves, and possibly humility, if done right.

5. Practice forgiveness – This might take some reinterpreting in terms of learning, but I do believe there are lessons of forgiveness in the PBL classroom. Students who expect themselves to learn everything the first time and when they don’t, feel stupid, need to forgive themselves and realize that learning is an ongoing process. Learning takes time and maybe needs more than one experience with a topic to see what the deeper meanings and understandings really are. Since PBL is not just a repetitive, rote teaching method, students need to learn how to be patient and forgiving of their own weaknesses as a learner and take time to see themselves as big picture learners.

6. Have a sense of purpose – This habit is about “big picture” purpose and looking at a plan. From the research that I did, I also found that PBL brings together many topics in mathematics, allowing students to see the “big picture” connections between topics much better than traditional teaching does. The decompartmentalization that occurs (as opposed to compartmentalizing topics into chapters in a textbook) is confusing at first because they are not used to it, but eventually students see how topics thread together. Just the other day in my geometry class we were doing a problem where they were asking to find as many points as possible that were 3 units away from (5,4) on the coordinate plane. A student in the class asked, “is this how we are going to get into circles?” The whole class was like “Oh my gosh, it is, isn’t it?” Bam, sense of purpose.

All in all, I feel that PBL meets Moran’s criteria of “resilience characteristics” in ways in which it allows students to practice these habits on a regular basis.  So not only does PBL help students learn collaboration, communication and creativity, but perhaps they will see the benefits over time in learning how to move forward from a setback – just a little.

 

Sharing in Chicago! PME-NA 2013

So tomorrow I’m off to PME-NA 2013 in Chicago which is one of my most favorite conferences for mathematics education research.  I will be presenting my research findings from my dissertation on Saturday morning and I’m so lucky to be going.  I’ve posted my PMENA handout  for anyone interested in having it.  I’m also posting  the powerpoint on my slideshare site.

Teaching Students to Become Better “Dancers”

So the other day I read a tweet by Justin Lanier that really sparked my interest.

 We all know the scenario in classroom discourse where a student asks a question – a really great question – and you know the answer, but you hedge and you say something like, “That’s a great question! I wonder what would happen if…”  So you reflect it back to the students so that they have something to think about for a little while longer, or maybe even ask a question like “Why would it be that way?” or “Why did you think or it like that?”  to try to get the student to think a bit more.  But what Justin, and the person who coined the phrase “authentic unhelpfulness” Jasmine Walker (@jaz_math), I believe were talking about was hedging because you really don’t know the answer – sincere interest in the uniqueness of the question – not because you’re so excited that student has helped you move the conversation forward, but because of your own excitement about the possibilities of the problem solving or the extension of the mathematics.

I think what got me so excited about this idea was how it connected to something that I was discussing earlier this summer with a group of teachers in my scaffolding in PBL workshop in late June.  In a PBL curriculum, the need to make sure that students have the right balance of scaffolded problems and their own agency is part of what Jo Boaler called the “Dance of Agency” in a paper she wrote in 2005 (see reference).  My understanding of this balance goes something like this:

(c) Schettino 2013

So initially, the student is confused (or frustrated) that the teacher refuses to answer the question although you are giving lots of support, advice and encouragement to follow their instincts.  The student has no choice but to accept the agency for his or her learning at that point because the teacher is not moving forward with any information.  But at that point usually what happens is that a student doesn’t feel like she has the authority (mathematical or otherwise) to be the agent of her own learning, so she deflects the authority to some other place.  She looks around in the classroom and uses her resources to invoke some other form of authority in problem solving.  What are her choices?

She’s got the discipline of mathematics – all of her prior knowledge from past experiences, she’s got textbooks, the Internet, her peers who know some math, other problems that the class has just done perhaps that she might be able to connect to the question at hand with previous methods that she might or might know how they work or when they were relevant – that discipline has had ways in which it has worked for her in the past and lots of resources that can help even if it may not be immediately obvious.

But she’s also got her own human agency which is most often expressed in the form of asking questions, seeing connections, drawing conclusions, thinking of new ideas, finding similarities and differences between experiences and thinking about what is relevant and what is not.  These pieces of the puzzle are not only important but a truly necessary function of the “dance of agency” and imperative to problem solving.

Interweaving both of these types of agency (and teaching kids to do this) have become more important than ever.  Yes, being able to use mathematical procedures is still important, but more important is the skill for students to be able to apply their own human agency to problem and know how and when to use which mathematical procedure, right?  This “dance” is so much more important to have every day in the classroom and if what initiates it is that deflection of authority then by all means deflect away – but the more we can “dance” with them, with “authentic unhelpfulness” and sincere deflection because we need to practice our own human agency, the more we are creating a true community of practice.

Boaler, J. (2005). Studying and Capturing the complexity of practice – the Case of the ‘Dance of Agency’

Anja S. Greer Conference 2013

What a great time we had this week in my courses!  I am so excited by all of the folks that I met and the CwiC sessions of other leaders that I went to.  Pretty awesome stuff presented by Maria Hernandez from NCSSM, my great colleague Nils Ahbel, Tom Reardon, Ian Winokur, Dan Teague, Ken Collins and many others.  I was so busy that I didn’t get to see many other people’s sessions so I feel somewhat “out of it” unfortunately.

I want to thank everyone that came to my CwiC’s and remind them to be sure to go and pick up my materials on the server before they leave.

For my participants – here are the links to the course evaluations:

Moving Forward with PBL: Course Evaluation

Scaffolding and Developing a PBL Course:  Course Evaluation

Linking Theory to Practice: A Shout-Out to ‘savedabol’

This past January, I gave a key-note address at the ISOMA conference in Toronto and posted my slides from that talk on my academia.edu site that I thought would be a good place for me to easily give other people access to my work. (along with my website).  Academia.edu is great because it gives you lots of information about the stats of surfers who come and look at your information.  All of a sudden I saw that this powerpoint had more than something like 400 views and I couldn’t believe it.  I had to see who was searching and looking at this slideshow.

I quickly realized that someone had seen it, liked it and posted something about it on reddit.  There were only a few comments but one of them went something like this:

“I think the single worst part of being a teacher is sitting through PowerPoints like this, while some earnest non-classroom pedagogue tells us the bleeding obvious.”

Whooo – that one stung…my first instinct was to try and find out who that person was and defend myself to the ends of the earth.  Anyone who calls me a non-classroom pedagogue deserves to be righted…but then I kept reading…and someone with the alias ‘savedabol’ wrote this:

‘Carmel Schettino (the author) led a seminar I took at the Exeter math conference last summer. She is incredible. I can assure you that she is not a non-classroom pedagogue. She has been in the classroom nonstop for at least 20 years (that I know of). She is particularly scholarly when it comes to PBL and other ed topics, but that doesn’t make her irrelevant to what we do every day. Near the end she gives some great resources.’

I can’t tell you how affirmed I felt by ‘savedabol’ and I want to just let them know how nice that was of them to share their thoughts about my work with them.  I have been in the classroom non-stop since 1990 (except for two terms of maternity leave and one term of a sabbatical when I was a full-time student myself) and I pride myself in researching as much as possible about what I do.

I do wish that the first poster had had the chance to hear me speak instead of jumping to the conclusions they had – and it definitely got me thinking about something that was discussed last year at the PME-NA conference in October 2012.  I was one of maybe just a few people in the special category of math teacher/educator/researcher/doctoral students at this research conference where many of the math research folks were talking about ways in which they could breach the great divide of the theory people (them) and the practice people (us).

For many years I have lived this double life of both theory and practice and I have to say, I love it.  Having just finished up my Ph.D. and teaching full time was probably one of the toughest things I’ve had to do in my life, but having my mind constantly in both arenas has only helped me be a better teacher and a better researcher.

Jo Boaler is a great researcher at Stanford University who is doing great work in outreach between theory and practice this summer by offering a free online course called “How to Learn Math.”  It’s a course for k-12 teachers that is grounded in the most recent research in math education.  What a great idea!  She is sharing some of her wisdom freely online with k-12 teachers who want to spend some time learning about new ideas themselves.  I know I’m in.

In August 2008, the NCTM put together a special Research Agenda Project to work on recommendations for just this cause and you can see their report here.  One of the major recommendations that came out of their work was to not only emphasize the need for communication between researchers and practitioners, but in my view to help them realize that this communication would benefit both parties equally.  We all have something to share with each other and I know that I appreciate every classroom practitioners’ experiences.  I learn something from every teacher that ends up in my workshop every summer and often end up using many of their ideas as they do mine.

So let’s keep supporting each other both in real life and virtually, and realize that often times, the “bleeding obvious” is something that needs to be stated and discussed over and over again to be sure that we are still talking about it with the right people.

PBL – Students making Mathematical Connections

As someone who has used Problem-Based Learning for almost 20 years and sad to say has never been part of a full-fledged Project-Based Learning curriculum, what I know best is what I call PBL (Problem-Based Learning).  I know there is a lot of confusion out there is the blogosphere about what is what, and with which acronyms people use for each type of curriculum.  I did see that some people have been trying to use PrBL for one and PBL for the other, but I guess I don’t see how that clarifies – sorry.

So when I use the acronym PBL in my writing I mean Problem-Based Learning and my definition of Problem-Based Learning is very specific because it not only implies a type of curriculum but an intentional relational pedagogy that I believe is needed to support learning:

Problem-Based Learning (Schettino, 2011) – An approach to curriculum and pedagogy where student learning and content material are (co)-constructed by students and teachers through mostly contextually-based problems in a discussion-based classroom where student voice, experience, and prior knowledge are valued in a non-hierarchical environment utilizing a relational pedagogy.

Educational Psychologist and Cognitive Psychologists like Hmelo-Silver at Rutgers University have done a lot of research on how students learn through this type of scaffolded problem-based curriculum dependent on tapping into and accessing prior knowledge in order to move on and construct new knowledge.  There was a great pair of articles back in 2006/2007 where Kirschner, Sweller & Clark spoke out against problem- and inquiry-based methods of instruction and Hmelo, Duncan and Chinn responded in favor.  I highly recommend reading these research reports for anyone who is thinking of using PBL or any type of inquiry-based instruction (in math or any discipline).  It really helps you to understand the pros and cons and parent and administrator concerns.

However, after you are prepared and know the score, teachers always go back to their gut and know what works for their intuitive feeling on student learning as well.  For me, in PBL, I look at how their prior knowledge connects with how, why and what they are currently learning.  One of the best examples of this for me is a sequence of problems in the curriculum that I use which is an adaption from the Phillips Exeter Academy Math 2 materials.  I’ve added a few more scaffolding problems (see revised materials) in there in order to make some of the topics a bit fuller, but they did a wonderful job (which I was lucky enough to help with)and keep adding and editing every year. The sequence starts with a problem that could be any circumcenter problem in any textbook where students use their prior knowledge of how to find a circumcenter using perpendicular bisectors.

“Find the center of the circumscribed circle of the triangle with vertices (3,1), (1,3) and (-1,-3).”

Students can actually use any method they like – they can use the old reliable algebra by finding midpoints, opposite reciprocal slopes and write equations of lines and find the intersection points.  However, I’ve had some students just plot the points on GeoGebra and use the circumcenter tool.  The point of this problem is for them to just review the idea and recall what makes it the circumcenter.  In the discussion of this problem at least one students (usually more than one) notices that the triangle is a right triangle and says something like “oh yeah, when we did this before we said that when it’s an acute triangle the circumcenter is inside and when it’s an obtuse triangle the circumcenter is outside.  But when it’s a right triangle, the circumcenter is on the hypotenuse.”

Of course then the kid of did the problem on geogebra will say something like, “well it’s not just on the hypotenuse it’s at the midpoint.”

 

Dicussion will ensue about how we proved that the circumcenter of a right triangle has to be at the midpoint of the hypotenuse.

A day or so later, maybe on the next page there will be a problem that says something like

“Find the radius of the smallest circle that surrounds a 5 by 12 rectangle?”

Here the kids are puzzled because there is no mention of a circumcenter or triangle or coordinates, but many kids start by drawing a picture and thinking out loud about putting a circle around the rectangle and seeing they can find out how small a circle they can make and where the radius would be.  When working together oftentimes a student see a right triangle in the rectangle and makes the connection with the circumcenter.

A further scaffolded problem then follows:

“The line y=x+2 intersects the circle  in two points.  Call the third quadrant point R and the first quadrant point E and find their coordinates.  Let D be the point where the line through R and the center of the circle intersects the circle again.  The chord DR is an example of a diameter.   Show that RED is a right triangle.”

Inevitably students use their prior knowledge of opposite reciprocal slope or the Pythagorean theorem.  However, there may be one or two students who remember the circumcenter concept and say, “Hey the center of the circle is on one of the sides of the triangle.  Doesn’t that mean that it has to be a right triangle?”  and the creates quite a stir (and an awesome “light bulb” affect if I may say so myself).

A few pages later, we discuss what I like to call the “Star Trek Theorem” a.k.a. the Inscribed angle theorem (I have a little extra affection for those kids who know right away why I call it the Star Trek Theorem…)

I will always attempt to revisit the “RED” triangle problem after we discuss this theorem.  If I’m lucky a student will notice and say, “Hey that’s another reason it’s a right triangle – that angle opens up to a 180 degree arc, so it has to be 90.”  and then some kid will say “whoa, there’s so many reasons why that triangle has to be a right triangle”  and I will usually ask something like, “yeah, which one do you like the best?” and we’ll have a great debate about which of the justifications of why a triangle inscribed in a circle with a side that’s a diameter has to be right.  So who are the bigger geeks, their teacher who names a theorem after Star Trek or them?

References:

Kirschner, P. A., Sweller, J., & Clark, R. E. (2006). Why minimal guidance during instruction does not work: An analysis of the failure of constructivist, discovery, problem-based, experiential and inquiry-based teaching. Educational Psychologist, 41(2), 75-86.

 

Hmelo, C. E., Duncan., R.G., & Chinn, C. A. (2007). Scaffolding and achievement in problem-based and inquiry learning: A response to Kirschner, Sweller and Clark (2006). Educational Psychologist, 42(2), 99-107.

 

Affirming the “Un-fixing” of the roles in Mathematics

So after nine, long hard years, I am finally at a point where I am proud to say, “I’m finished!”  Woo-hoo and hurrah, tonight I will submit my dissertation electronically and you can call me Dr.  Reading over my work has been probably one of the most fulfilling acts of my professional life, as was defending my dissertation last week.  I can’t believe how fun it actually was – too true.  When you are passionate about a topic, it never gets old. Then, just today my advisor sends me an article that was published in the Harvard Education Letter titled, “Changing the Face of Math”which strangely sounds so much like what I’ve been working on for so long.  It talks about the current state of the way students create identities in mathematics in the U.S. and how this is detrimental to their beliefs about what they can do and be in the mathematics classroom and beyond.  Sadly, as high school teachers, half of our job is undoing the mathematical identity that the system has put in place all the years before they have come to us. In my dissertation, I wrote about not only this identity question but the difficulty in how American society has such a gendered, dichotomous view of mathematics that even those of us who attempt to move past the stereotypes because of our love of mathematics end up with difficult situations to work against.  For some, it is so difficult that we end up giving up and choosing the easier path – the girl who loves physics but choose biological engineering because she feels like she belongs there.  Or the young woman who goes to college to be a math major, but ends up in International communications because the classes were not taught in a way that worked for her learning style.  Or the weak female mathematics student who doesn’t even consider taking another math class in college because of the negative view of her abilities years ago. In this article they say,

“Math education experts say we’re in crisis and that traditional approaches of treating math like a cold-blooded subject amid the warm and engaging world of K–12 schooling are a big part of the problem. Narrow cultural beliefs about what math success looks like, who can be good at it, and what it’s used for are driving students to approach the subject with timidity—or not at all.”

Which was so affirming because it was the major educational research question that motivated my dissertation!  I love it.  Allowing all underrepresented students, not just girls to find ways to change the way they view themselves as math students by changing the way we teach mathematics would be revolutionary, and so many people are doing it.  I am proud to be a part of this movement to “unfix” the gendered, dominant, presumed ways of mathematics learning and open it up to more subjective, creative and collaborative thinking processes. It’s a great time to be a revolutionary!