Category: Research

Shared Failure as a PBL Experience

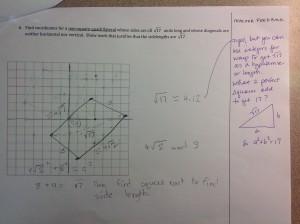
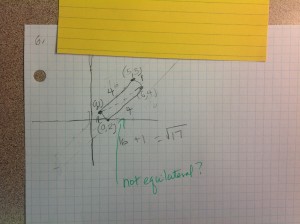
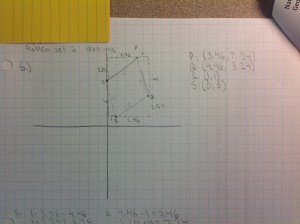
“A self-compassionate attitude could help us feel comforted when we witness the fallibility of other humans.”

Newman, 9/4/19 Greater Good Magazine

This is the conclusion of a research study that was done by researchers at the University of Waterloo, when they asked 100 recruited students to record a video about themselves to be rated on a scale from 1-9 on how “great” they were (see study for more details).

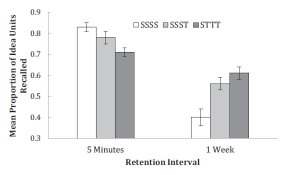
Unbeknowst to them, there were no objective observers, the study actually began when students were shown peers’ scores sometimes mediocre and sometimes outstanding. The question really was “how do you react when you have a sense of failure in the face of others’ success?” Of course, the findings were interesting. It depended on the person. If they were the type of person that had a great sense of how life is wrought with failure and learning from our mistakes, they were more likely to have an adaptable, compassionate, and sympathetic reaction to others’ failure. However, if the student had the habit of being hard on themselves for failing, that is often what they reflected onto others and had a hard time being sympathetic.

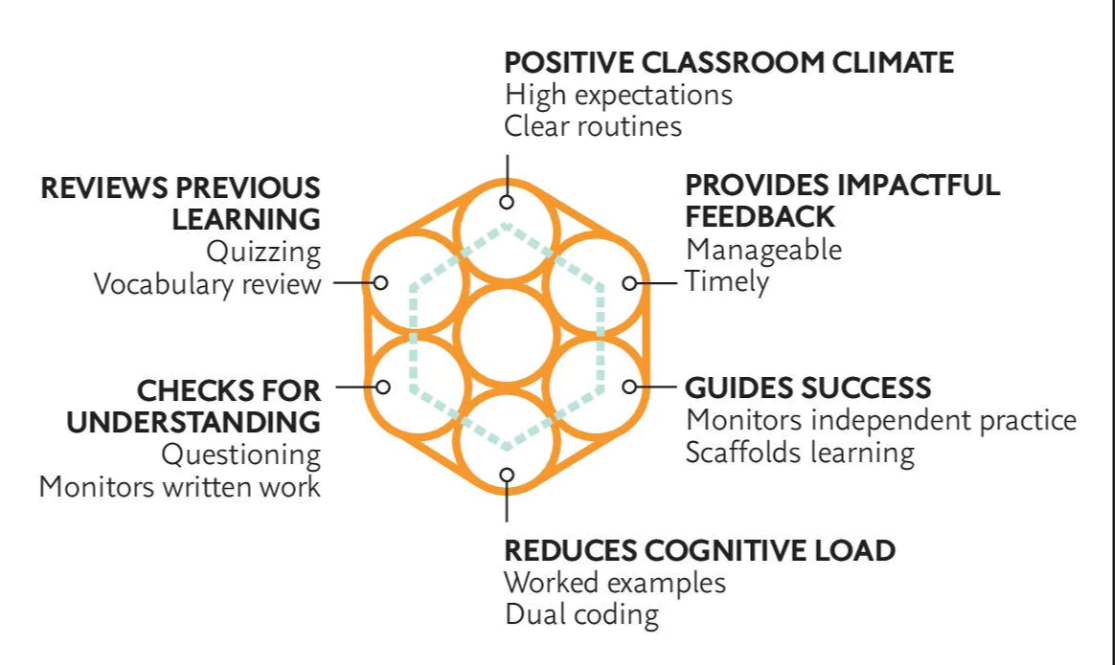
As I read this research study, I could not help but put all of this into the context of the PBL classroom. I immediately thought “this is why whole-class discussion with sharing authority is so important.” In order for the failure of the presenter to be shared by the class and experienced as the shared experienced of failure, students should hear ideas, discuss the pros and cons and loopholes and catch the mistakes together. This could not have happened in isolation or in pairs (caveat: not to say that whole class discussion is the only way it can happen or is the only PBL should happen). The shared experience of confusion, being sympathetic to the confusion, the risk-taking of embarassment or being wrong, needs to happen for everyone to say “I know what that feels like.”

Of course, this needs to be done a classroom that fosters the idea that this is a good thing – we need to make mistakes and learn from them – in a safe, non-hierarchical environment where status and positioning are being closely reflected upon by the teacher. What this study shows is that the other mindset (e.g. fixed, as we’ve come to call it) won’t necessarily embrace the shared failure and could make the shared failure counterproductive. This is a hugely important part of the dynamics of a PBL classroom.

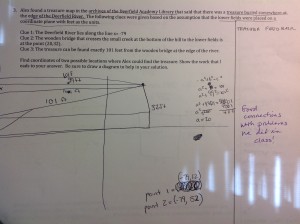
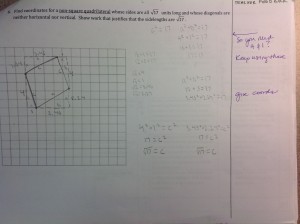
I can’t help but recall a student that I interviewed for my dissertation research and how she captured her feeling about shared failure, in that by contributing ideas, the failures or mistakes become a shared success:

You could kind of add in your own perspective, and kind of give you this sense like, “Ooooh, I helped with this problem” and then another person comes in and they helped with the problem, and by the end, no one knows who solved the problem. Like, everyone contributed their ideas to this problem and you can look at this problem on the board and you can maybe only see one person’s handwriting, but behind their handwriting is everyone’s ideas. So yeah, it’s a sense of “our problem.” It’s not just Karen’s problem, it’s not just whoever’s problem, it’s “our problem.”

Kaley, Schettino Dissertation 2013

How do you use empathy to teach math?

1 Comment

This post is part of the Virtual Conference on Mathematical Flavors, and is part of a group thinking about different cultures within mathematics, and how those relate to teaching. Our group draws its initial inspiration from writing by mathematicians that describe different camps and cultures — from problem solvers and theorists, musicians and artists, explorers, alchemists and wrestlers, to “makers of patterns.” Are each of these cultures represented in the math curriculum? Do different teachers emphasize different aspects of mathematics? Are all of these ways of thinking about math useful when thinking about teaching, or are some of them harmful? These are the sorts of questions our group is asking.

 

One of the things that is interesting about teaching with PBL is how students often describe enjoying this type of math class more than others they have had in the past. It’s hard for students to paint a picture of what it is that produced their enjoyment.  The interesting thing is that it is often not the mathematics they enjoy, but the class itself – the interactions and relationships between the people in the class, and should they be solving some interesting problems that pertain to mathematics, that’s pretty great, too.

What one girl, Isabelle, described enjoying about my class once, was the way in which she saw mathematics as no longer black and white – with only the teacher’s information as what counts.  In a research interview, I asked her to describe for me what that was like:

Isabelle:  Like it’s, if you have a question you can just ask it and then that can lead into, like, some conversation or [the teacher] can ask a question and then kind of leaves it out there for us, the kids, to answer it, so…

Ms. S:  OK, and why do, why do you like that better?

Isabelle:  Um, because it’s not so uptight and [laughs], like it’s not like focused, “memorize all of this stuff…”

Ms. S:  Hmm

Isabelle:  It’s more relaxed, and that helps me learn better I think.

Isabelle’s more traditional view of the mathematics classroom with its “uptight” and rigid nature reminds her of memorizing facts and formulas and she stated that she responds better to a classroom that, in her eyes, is more “relaxed” and interactive allowing her views and responses to matter.  This is extremely consistent with Frances Maher and Mary Kay Thompson’s (2001) view of the feminist classroom’s responsibility to “deliberately position students as academic authorities” in order to allow them the input for the feeling that their responses matter, but so that that they do not “dismiss their own emerging sense of themselves.”  Also, Isabelle’s feelings are consistent with what Fox Keller (1985) once called “dynamic objectivity” which she defined in terms of how we might be inclined to think about the idea of integrating student input with factual mathematical knowledge.

Dynamic objectivity is a form of knowledge that grants to the world around us its independent integrity but does so in a way that remains cognizant of, indeed relies on, our connectivity with that world.  In this, dynamic objectivity is not unlike empathy, a form of knowledge of other persons that draws explicitly on the commonality of feelings and experience in order to enrich ones’ understanding of another in his or her own right (Fox Keller, p.117).

We can view this more flexible way of viewing knowledge as necessary for including students like Isabelle who find the more rigid mathematics classroom not conducive to learning.  She would rather remain connected to the material and the persons in the classroom with her in order to facilitate learning for herself.  Many students truly enjoy the fact that students are the contributors to the knowledge and part of the authority presence in the classroom.  Because of the openness to the dynamic objectivity of the knowledge, the students are able to accept that their input is valuable.  When I asked Isabelle why she thought the students felt so compelled to participate in a PBL classroom, she had this to say:

Ms. S:  Yeah, there’s almost a guarantee that people will… I wonder why? I wonder what guarantees that everyone will have something to say.

Isabelle:  Well [both laugh] it’s probably just because geometry has like twenty… like a lot of different ways to do certain problems so there’s a lot of variations in the way that people do them, so…

Ms. S:  Hmm.

Isabelle:  That might be it, or it might just be that people feel comfortable in the situation they’re in to participate and it’s not like, “OK nobody ask questions so we can leave now.”

Ms. S: [laughs]  Yeah. Ok. So there’s a certain amount of like motivation to want to talk about it?

Isabelle:  Yeah.

Ms. S:  because it’s like interesting to hear what other people did? [pause] Um, yeah, I can’t figure that out.

Isabelle:  I think everybody like shares the same curiosity level and like when somebody… like I know in our physics class he never tells us the answer to questions and it drives everybody crazy…

Ms. S:  Huh…

Isabelle:  And then we all start talking about it to try and figure out if like we can find out the answer ourselves so and the same thing happens in my math class so…

Ms. S:  Yeah?

Isabelle:  I think it’s just the motivation to find the right answer and like, because I know everybody in my class wants to understand.

Isabelle had described a mathematics classsroom culture with a tacit understanding of the dynamic objectivity of the part that students play in the formation of knowledge.  When presented with a problem where the solution is unknown and the teacher presumes a certain lower level of authority than the students, the students take on a higher level of responsibility and curiosity in finding solutions and methods for those solutions.  Being open to a view of dynamic objectivity and the empathy that it needs, allows many students to have their comfort in this type of learning environment and fosters more equity in learning for students who have previously been disenfranchised in mathematics and science classes.

 

Fox Keller, Evelyn, (1985). Gender and Science. New Have: Yale University Press.

Maher, F. A., & Thompson Tetreault, M. K. (2001). The Feminist Classroom. New York: Rowman & Littlefield Publishers, Inc.

Reducing Cognitive Load in PBL

2 Comments

One of the things that I have been thinking about for a very long time is the idea of those who oppose PBL.  Namely those who prescribe to behaviorist and cognitive scientist theories of learning, which I know a great deal about because of my doctoral work.  So many teachers, parents and others have asked me about this over the past 25 years that you’d think I would have an answer.  I know I have thoughts but I do want to do more research in this area.

I do not pay lip-service to the ideas of cognitive load theory for sure and definitely respect those who follow these ideas.  I do think there is a place for thinking about this theory in PBL, but not an argument for why NOT to do it.  At its heart though, I believe the learning outcomes that are important in the different types of theory (CLT vs. constructivist learning for example) is what ends up differentiating them and also the way the knowledge is constructed.  I do believe in the importance of reducing the Cognitive Load for students so that their long-term memory can be triggered and practiced.

So I do believe there is a place for this in PBL – it just hasn’t been discussed a great deal.  There is always this us vs. them notion that one is right and the other is wrong – it comes from very strong belief systems and I totally understand where they are coming from.  However, if PBL is done well in a scaffolded, structured way, I believe that you can both reduce cognitive load and also ask students to think creatively.

Here is an image I saw from an article in the Guardian recently entitled Teachers: Your Guide to Learning Strategies that Really Work by Carl Hendrick. This graphic is describing the six ways to make your classroom best-ready for learning.

 

Positive Class room climate

 

When I was looking at this, the first thing I thought of is “This is my PBL classroom.”  However, I could tell there would have to be some discussion of the “reducing cognitive load” part.  All the other aspects, I believe you can find in some other blogpost of mine somewhere.  In a PBL classroom, the way that students get timely feedback is in so many ways (see my rubrics, journals, etc.).  The nightly homework is the scaffolding of learning and monitoring of independent practice – again when done well.  I won’t go through every one of these, but would love your takes (in the comments below) on each of them.

So then, how can we talk about reducing cognitive load in PBL – where is lecture and worked problems that the teacher does?  I would argue that the cognitive load is reduced by the scaffolding of the problems in the curriculum.  In other words, by triggering students’ prior knowledge the cognitive load is reduced in such a way that they are remembering something they have learned from the past, and then being asked to look at something new.  The “something new” goes through many phases of problems – concrete, multiple representations, all the way through to abstract – in order to slightly build up the cognitive load.  Again, this is all if it is done well and very deliberately with the idea of not to overload students’ thinking but to help to build the schemas that are needed for constructing knowledge both individually and socially.

The problems are worked by the students, yes – I will give you that.  But it is the teacher’s responsibility to make sure that the steps are correct, students get feedback on their thoughts and ideas, that on the board at the end of the discussion is a correct solution and so much more.  What this type of teaching does, in my view is both reduce cognitive load to a point, yet also allow students to gain agency and ownership of the material through their prior knowledge and experience.

Something else that Mr. Hendrick says in his article is:

“Getting students to a place where they can work independently is a hugely desired outcome, but perhaps not the best vehicle to get there. Providing worked examples and scaffolding in the short-term is a vital part of enabling students to succeed in the long-term.”

And I would ask, what does students’ success mean in this framework?  Some studies have shown that worked examples are beneficial in only some cases for student learning.  Others have shown that students that are taught with worked examples out-perform those who received individual instruction.  I could go on and on with the studies contradicting each other.  But what if they weren’t in contradiction?  What if there was a way that they could work together – both reducing cognitive load and also giving students agency and voice in the classroom?  Allowing students the freedom to become independent problem solvers but also scaffolding the learning in such a way that their cognition was not overloaded?  Maybe I’m an optimist, but I do believe there is a way to do both.

I’ve looked at life from both sides now…

4 Comments

This past July, I spent a few days at the MAA Mathfest in Chicago for the first time. The main reason I went was because the Academy of Inquiry-Based Learning was having a Conference within the Mathfest with the theme of “Diversity in IBL.”  IBL is generally what college faculty call the type of teaching and learning that many of us at the secondary level has been calling PBL for years.  I was so interested to hear many mathematics professors talking about the struggles of writing curriculum, dealing with facilitating discussion, using writing – all of the same parts of this type of teaching that we may have been talking about for so any years.  I highly suggest that we could benefit from talking to each other.  If you would like to get involved with this movement, Stan Yoshinobu, the Director of the Academy of Inquiry-Based Learning, has put forth some challenges for his community.  Check them out.

One of the most interesting talks that I attended was by a professor from Denison University, Lew Ludwig, titled, “Applying Cognitive Psychology to the Mathematics Classroom.”  As a devout social constructivist, I generally like going to talks where I can learn more about other views of education.  Seeing both sides definitely helps me understand many of the views of my colleagues and see if evidence supports my own perspective. Ludwig had published a review of another article that was titled, “Inexpensive techniques to improve education:  Applying cognitive psychology to enhance educational practice”(Roediger and Pye, 2012).

Basically, the presentation summarized three simple techniques that cognitive psychology had evidence helped student learning. The three techniques were called

  1. The distribution and interleaving of material and practice during learning.
  2. Frequent assessment of learning (test-enhanced learning, continual assessment)
  3. Explanatory questioning (elaborative interrogation and self explanation; having students ask themselves questions and provide answers or to explain to themselves why certain points are true).

In the original article, the authors write:

“Repetition of information improves learning and memory. No
surprise there. However, how information is repeated determines
the amount of improvement. If information is repeated back to back
(massed or blocked presentation), it is often learned quickly but
not very securely (i.e., the knowledge fades fast). If information is
repeated in a distributed fashion or spaced over time, it is learned
more slowly but is retained for much longer”

When this was reported, I was first in shock.  I couldn’t believe I was hearing something in a presentation about Cognitive Psychology that was actually supported by the definition of PBL that I use.  The curriculum I use takes the idea of looking at topics and teaching them over a longer time span, but distributed among other topics.  I have called this decompartmentalization of topics, which helps students see the connectedness of mathematics.

The second idea, consistent assessment, is based on the concept that testing is not really a great measure of how much a student has learned, but it actually solidifies the learning that has occurred.  So three groups of students were given different ways of learning by reading a passage of information. The first group read a passage four times. The second group read the passage three times and had test.  The third group read the passage once and was tested three times.  Their performances on tests on the information in the passage 5 minutes later and then one week later.

Diagram of retention testing research
from Roediger & Pye (2012) p.245

So if we connect the idea that testing is not the best method of seeing how much students have learned and the fact that consistent assessment actually helps students retain their knowledge, what I do in my PBL classrooms, is not only “test” but do all sort of forms of assessment (writing, oral assessment, hand-in homework with feedback, labs, quizzes, problem sets, self-assessment, etc.) alternately throughout the term.  There is probably not a week where students are not assessed in at least 2 ways. I feel that this has led students to have good retention of material and the assessments are strong measurements of their learning.

The last one was the one I was most excited to hear about – explanatory questioning.  This seemed to give students so much more responsibility for their own learning than traditional cognitive psychology as I had understood it.  The authors of this study claim that explanatory questioning can be broken in to two areas:

Elaborative Interrogation – students generating plausible explanations to statements while they are studying and learning.  This speaks directly to the idea of mathematical discussion and how students generate explanations when they ask themselves “why?”

Self-Explanation – students monitoring their learning and describing, either aloud or silently some features of their learning.  This idea can be found all over the PBL classroom but in mine, it’s generally found most in metacognitive journaling where students use self-explanation the most.

“Obviously, the elaborative interrogation and self explanation are related because both strategies encourage or even require students to be active learners, explaining the information to themselves (perhaps rephrasing in language they understand better) or asking themselves why the information is true.”

I honestly couldn’t believe what I was reading – this is an article on educational methods based on cognitive psychology that is suggesting that we require students to be active learners and “explain the infomation to themselves”?  This is lunacy.  I have been teaching for 25 years where students have been complaining to their parents that they have had to explain things to themselves – who would’ve known that I was applying cognitive psychology?

My guess is that these ideas are only enhanced by the social aspect of the classroom and other constructivist ideas – clearly the constructivitst classroom in enhanced by or agrees with some of these cognitive psychology methods as well.  Listening to both sides of the theories is actually helpful and I’m seriously going to continue doing this! Although I never thought that there might be strong connections between cognitive psychology theories and PBL, I do know that it’s life’s illusions I recall and I “really don’t know life, at all.”

Yours, Mine and Ours

Yesterday we had a speaker in our faculty meeting who came to talk to us about decision-making process in our school.  He spoke about the way some colleges, universities, independent schools are very different from businesses, the military, and other governing bodies that have to make decisions because we are made up of “loosely-coupled systems.” These are relationships that are not well-defined and don’t necessarily have a “chain of command” or know where the top or bottom may be.  They also don’t necessarily have a “go-to” person where, when a problem arises, the solution resides in that location.  The speaker said that this actually allows for more creativity and generally more interesting solution methods.

About mid-way through his presentation he said something that just resonated with me fully as he was talking about the way these systems come to a decision cooperatively.

“The difference between mine and ours is the difference between the absence and presence of process.”

Wow, I thought, he’s talking about PBL.  Right here in faculty meeting.  I wonder if anyone else can see this.  He’s talking about the difference between ownership of knowledge in PBL and the passive acceptance of the material in a direct instruction classroom.

Part of my own research had to do with how girls felt empowered by the ownership that occurred through the process of sharing ideas, becoming a community of learners and allowing themselves to see others’ vulnerability in the risk-taking that occurred in the problem solving.  The presence of the process in the learning for these students was a huge part of their enjoyment, empowerment and increase in their own agency in learning.

I think it was Tim Rowland who wrote about pronoun use in mathematics class (I think Pimm originally called it the Mathematics Register). The idea of using the inclusive “our” instead of “your” might seem like a good idea, but instead students sometimes think that “our” implies the people who wrote the textbook, or the “our” who are the people who are allowed to use mathematics – not “your” the actual kids in the room.  If the kids use “our” then they are including themselves.  If the teacher is talking, the teacher should talk about the mathematics like the are including the students with “your” or including the students and the teacher with “our”, but making sure to use “our” by making a hand gesture around the classroom.  These might seem like silly actions, but could really make a difference in the process.

Anyway,  I really liked that quote and made me feel like somehow making the process present was validated in a huge way!

Need Some Help Looking Forward

So I’m trying to figure out how to reach more people and thinking about the future of my professional development plans with PBL for all levels of teachers.  I’ve gotten some great feedback from people about the PBL Math Summit so far (from the two years we’ve had it) and I have some ideas about how to create some better online resources too.  If you have the time, and are interested in helping me out, would you please fill out this short survey about PD Needs for PBL Math Professional Development.  Also, tell others who could give me insights too.  Thanks so much for reading my blog and for also being inspired to be interested in PBL math teaching!

 

Considering Inclusion in PBL

It’s always refreshing when someone can put into words so eloquently what you have been thinking inside your head and believing for so long.  That’s what Darryl Yong did in his recent blogpost entitled Explanatory Power of the Hierarchy of Student Needs.  I feel like while I was reading that blogpost I was reading everything that I had been thinking for so long but had been unable to articulate (probably because of being a full time secondary teacher, living in a dorm with 16 teenage boys, being a mother of two teenagers of my own and all the other things I’m doing, I guess I just didn’t have the time, but no excuses).  Darryl had already been my “inclusive math idol” from a previous post he wrote about radical inclusivity in the math classroom, but this one really spoke to a specific framework for inclusion in the classroom and how in math it is necessary.

 

In my dissertation research, I took this idea from the perspective of adolescent girls (which, as I think towards further research could perhaps be generalized to many marginalized groups in mathematics education) and how they may feel excluded in the math classroom.  These girls were in a PBL classroom that was being taught with a relational pedagogy which focuses on the many types of relationships in the classroom (relationship between ideas, people, concepts, etc.)  – I did not look at it from the perspective of Maslow’s Hierarchy of Student Needs and this is really a great tool.

Interestingly,  I came up with many of the same results. My RPBL framework includes the following (full article in press):

  1. Connected Curriculum– a curriculum with scaffolded problems that are decompartmentalized such that students can appreciate the connected nature of mathematics
  2. Ownership of Knowledge – encouragement of individual and group ownership by use of journals, student presentation, teacher wait time, revoicing and other discourse moves
  3. Justification not Prescription– focus on the “why” in solutions, foster inquiry with interesting questions, value curiosity, assess creativity
  4. Shared Authority – dissolution of authoritarian hierarchy with deliberate discourse moves to improve equity, send message of valuing risk-taking and all students’ ideas

These four main tenets were what came out of the girls’ stories.  Sure many classrooms have one or two of these ideas.  Many teachers try to do these in student-centered or inquiry-based classrooms.  But it was the combination of all four that made them feel safe enough and valued enough to actually enjoy learning mathematics and that their voice was heard. These four are just a mere outline and there is so much more to go into detail about like the types of assessment (like Darryl was talking about in his post and have lots of blogposts about) the ways in which you have students work and speak to each other – how do you get them to share that authority when they want to work on a problem together or when one kid thinks they are always right?

The most important thing to remember in PBL is that if we do not consider inclusion in PBL then honestly, there is little benefit in it over a traditional classroom, in my view. The roles of inequity in our society can easily be perpetuated in the PBL classroom and without deliberate thought given to discussion and encouragement given to student voice and agency, students without the practice will not know what to do.  If we do consider inclusion in the PBL classroom, it opens up a wondrous world of mathematical learning with the freedom of creativity that many students have not experienced before and could truly change the way they view themselves and math in general.

Why Teachers Don’t Give Feedback instead of Grades, and Why We Should

7 Comments

First in a series of posts about my experiences with “Feedback Before Grades”

Holy Mackerel is all I have to say – Ok, well, no I have plenty more to say – but after about a week and a half of holing myself up with my colleague, Kristen McVaugh, (big shout-out to Ms McVaugh who is not only teaching PBL for the first time but was willing to dive into this amazing journey of alternative assessment with me this year too), I am totally exhausted, almost blind as a bat, partially jaded and crazy – but mostly ready for a drink.  This little looped video of Nathaniel Rateliff and the Night Sweats pretty much sums it up…

So here was our well-intentioned plan:  we wanted to start the year off with a different type of assessment.  I put out my feelers on twitter and asked around if anyone had a rubric for grading assessments where the teacher first gave only feedback and then allowed students to do revisions and then once the revisions were done the students received a grade. Kristen and I knew a few things:

  1. we wanted to make sure the revisions were done in class
  2. we wanted to make sure the revisions were the students’ own work (tough one)
  3. we wanted to give students feedback that they needed to interpret as helpful so that we weren’t giving them the answer – so that it was still assessing their knowledge the second time around
  4. we wanted to make sure that students were actually learning during the assessment
  5. we wanted students to view the assessment as a learning experience
  6. we wanted students to be rewarded for both conceptual knowledge and their skills in the problem solving too

So we created this rubric Initial Draft of Rubric for Grading.  It allowed us to look at the initial conceptual understanding the student came to the problem set with and also the initial skill level. Kristen and I spent hours and hours writing feedback on the students’ papers regarding their errors, good work and what revisions needed to be done in a back-handed sort of way.

Here are some examples:

Student 1 Initial Work

Student 2s initial work

Student 3 initial work

 

Some kids’ work warranted more writing and some warranted less.  Of course if it was wonderful we just wrote something like, excellent work and perhaps wrote and extension question.  The hard part was filling out the rubric.  So for example, I’ll take Student 3’s work on problem 6 which is the last one above. Here is the rubric filled out for him:

Student 3’s Rubric

You will notice that I put problem 6 as a 1 for conceptual understanding and a 2 for skill level (in purple). In this problem students were asked to find a non-square quadrilateral with side lengths of sqrt(17).  Student 3 was definitely able to find vertices of a quadrilateral, but he was unable to use the PT to find common lengths of sides.  I gave him feedback that looking at sqrt(17) as a hypotenuse of a right triangle (as we had done in class) would help a bit and even wrote the PT with 17 as the hypotenuse in the hope of stimulating his memory when he did the revisions.

The day of the revisions Student 3 was only capable of producing this:

Student 3 revisions

He followed my direction and used 4 and 1 (which are two integers that give a hypotenuse of 17, but did not complete the problem by getting all side lengths the same. In fact, conceptually he kind of missed the boat on the fact that the sqrt(17) was supposed to be the side of the quadrilateral altogether.

 

One success story was Student 2.  She also did this problem incorrectly at first by realizing that you could use 4 and 1 as the sides of a right triangle with sqrt(17) as the hypotenuse but never found the coordinates of the vertices for me. I gave her feedback saying there might be an easier way to do this because she needed vertices.  However, she was able to produce this:

Student 2s revision
Student 2s revision

Although she did not give me integer-valued coordinates (which was not required) and she approximated which officially would not really give sqrt(17) lengths it came pretty darn close! I was impressed with the ingenuity and risk-taking that she used and the conceptual knowledge plus the skill-level. Yes, most other kids just used some combination of 1’s and 4’s all the way around but she followed her own thought pattern and did it this way.  Kudos to student 2 in my book.

Next time I will talk about some of the lessons we learned, other artifacts from the kids’ work and what we are changing for next time! Oh yeah and some great martini recipes!

Why Can’t We All Just Get Along?: Some Inquiry Math Classes are not Content-less

Maybe it’s just how I am, or maybe I’m just always worried about what people are going to say about me, but I am hesitant to criticize other teachers publicly in the blogosphere. I’ve always felt this camaraderie with others once I’ve learned they were a teacher even if we are very different from each other – different disciplines, different pedagogical styles, different countries – there are still fundamental commonalities that even public and private school teachers have.

I just finished reading a KQED blogpost entitled “Do You Have the Personality to be an Inquiry-Based Teacher?” that sort of summarizes the theoretical qualities that the author feels a teacher who would teach with IBL would need to exhibit in order to successfully run a classroom. It’s kind of interesting – I’m not sure I agree with it, but respect the author for putting his ideas out there. I’ve been an inquiry/problem-based teacher for almost 20 years and I don’t think I exhibit all of the qualities listed, so I’m not sure it’s quite true.

Anyway, that’s not the point – at the end of the blogpost there are about 11 comments from people who are educators and many of them are quite negative and even degrading to the author:

“I earned a Ph.D. in Educational Psychology, but phrases like this one still baffle me: “…the divide between a transmission model and an inquiry model…” ”

“First, we need to make sure that we have at least a rudimentary understanding of the language in which we will be teaching. Second, we need to make sure we can write.”

“That is what’s wrong with you teachers.You want to do it your way.”

“Some of us have been doing this for decades, where were you?”

Whoa, Whoa, Whoa…cowboys…hold your horses. This guy is just writing an essay about something he believes in. What kind of role model are we being for our students if this is how we are reacting to something we don’t agree with? What happened to civil communication? I totally agree that people are allowed to comment and voice their opinions on someone else’s opinion, but there has to be a way to do it with respect and decency.

So I am going to try to model what I would like to see as a response to something I actually do disagree with. Here is a blogpost by a very respectable Professor in Canada, who I have to be totally honest, I do not know at all. I tried to learn as much as possible about him before writing a response to his blogpost in order not to make any assumptions about him (and not make a fool of myself in doing so), so I may be wrong about some of this information because I garnered it from different websites. It seems he is a research mathematician who is currently studying to get a teaching degree, but who lectures for mathematics courses at the college level. I cannot ascertain if he has any experience teaching at lower levels (like elementary or secondary). From his blogpost it does seem like he takes pride in the amount of background research he does, which again is very respectable and I appreciate in bloggers. He seems to care a lot about student learning and from his opinions on his blog he seems to lean towards being a behaviorist and cognitive theorist in terms of learning theories.

His latest blogpost is titled “The Content-less Curriculum” and it is a critique of the movement towards 21st Century skills being a part of the mathematics classroom. It does sound like Prof. Penfound is implying that with the inclusion of “soft skills” of collaboration, critiquing others work, problem solving,communication, etc. (i.e. the MPS for the CCSS) there must be a loss of mathematical content. In fact, he says that

“there must be a trade-off for the inclusion of “soft skills” activities into an already packed curriculum. So what gets removed from the curriculum then? Content knowledge.”

I would respectfully, but wholeheartedly disagree with this. By teaching with the PBL curriculum that I use, I have all of the college prep geometry curriculum I desire and I also concurrently am assessing and teaching the skills of problem solving and the so-called “soft skills” that he is implying are an add-on. I still give quick quizzes to make sure that students are up on their basic skills that are so important for basic problem solving (or else they wouldn’t be able to do the open-ended problems they are given).  The mathematics that students leave my courses having experienced is rich and leaves an impression on the way they think.

Making blanket statements about teachers implying that we all make choices that are not based in research or good practice is just not true. I actually invite you Prof. Penfound to come visit my classes and see my IBL/PBL classes in practice and let me know what you think of your opinions of the rigor of the mathematics that is discussed. Although we are most likely at different ends of the spectrum in terms of learning theories, I do believe that students have different needs and try to work with kids’ learning needs individually. However, I do believe as @danieldmccabe does that there are going to be new outcomes required of our ever-growing diverse body of graduates in the near future (or even present). I also have to say that I have thought rather thoroughly about the implementation of a teaching program which includes “soft skills” and even wrote a dissertation on it.

It is possible to balance content and practice skills and it is what I and many other classroom practitioners strive for. I do not deny that there are some practitioners out there that are confused about what problem-based and project-based learning outcomes should be especially with regard to secondary mathematics, but that is a subject for another blogpost.  The balance between content and practice skills we should strive for does not mean that one is more important or less important and in fact they both need to be assessed with the ultimate goal being to create independent problem solvers. From my experience this does not necessarily happen in a classroom where the educator does not take into consideration the so-called “soft skills.” But that statement is, of course, based on my 25 years of anecdotal classroom experience.

 

Handouts – Front and Center

I always try to make it easy for people to find both my slides and handouts when I give a talk – so Here’s my powerpoint presentation from my talk entitled, “Change the Classroom, Not the Students: Creating Equity with PBL”  which I’m giving today at the NCTM Annual Conference in New Orleans – great to be here.  I also have 2 handouts which include my framework for a relational PBL class and the results of my qualitative dissertation – I’d love to hear any comments and questions and start a discussion with PBL teachers. (I do not include the videos I used in this public version of the powerpoint, sorry)

[slideshare id=33364598&doc=changetheclassroomschettino-140410070229-phpapp02]

Schettino Framework Handout

Schettino Sample Problems Handout NCTM2014

There are actually a few talks here today that I would highly recommend and seem to be related to this topic of creating a classroom that allows for discussion and interaction at the level of creating equity.  One of them is on Friday, and is entitled “The Hidden Message: Micromessaging and Mathematics” and it seems to be about managing the way we talk to each other in the classroom and making sure all voices are heard.  I’m definitely going to that one!  Unfortunately, Jo Boaler is presenting at the exact same time as me!  I don’t know if I should take that as a compliment that I was put as the same time or not 🙁

Well, hope everyone has a great time!  Enjoy the conference!