Category: Problem based learning

Being Inspired & About Intuition

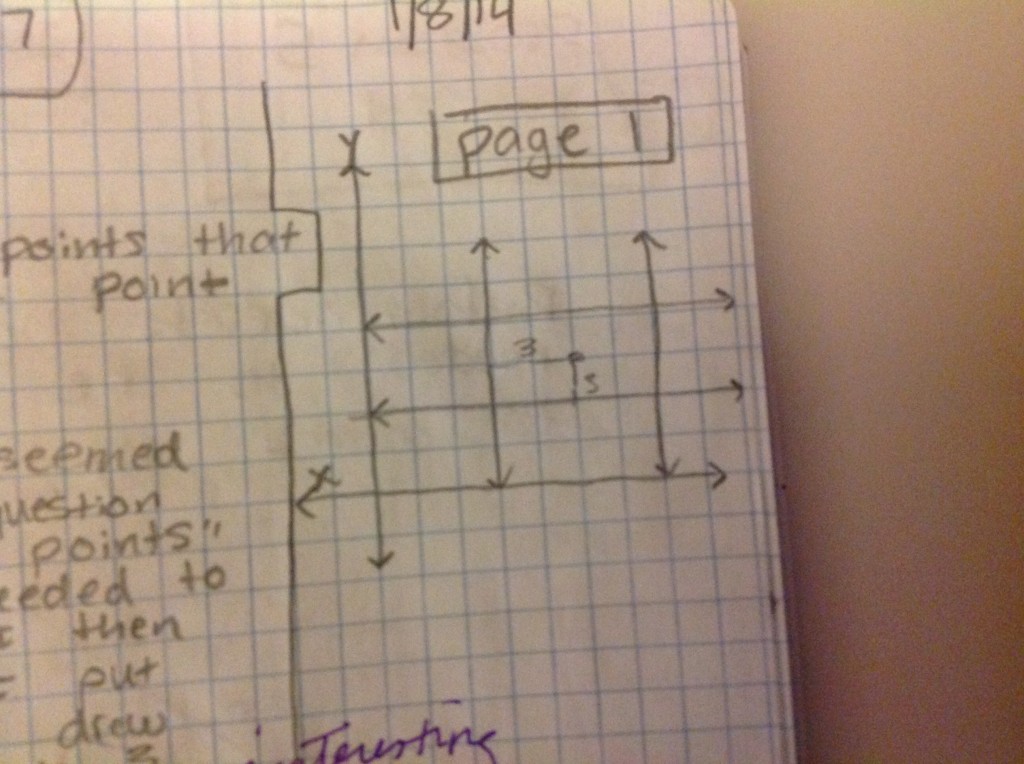
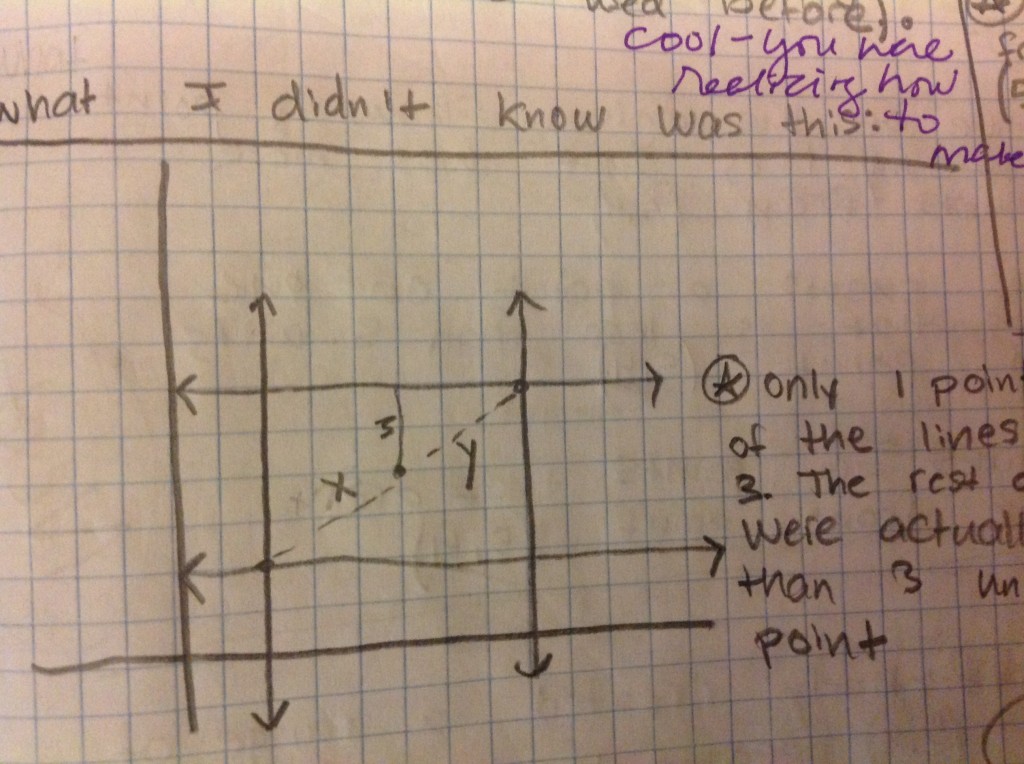
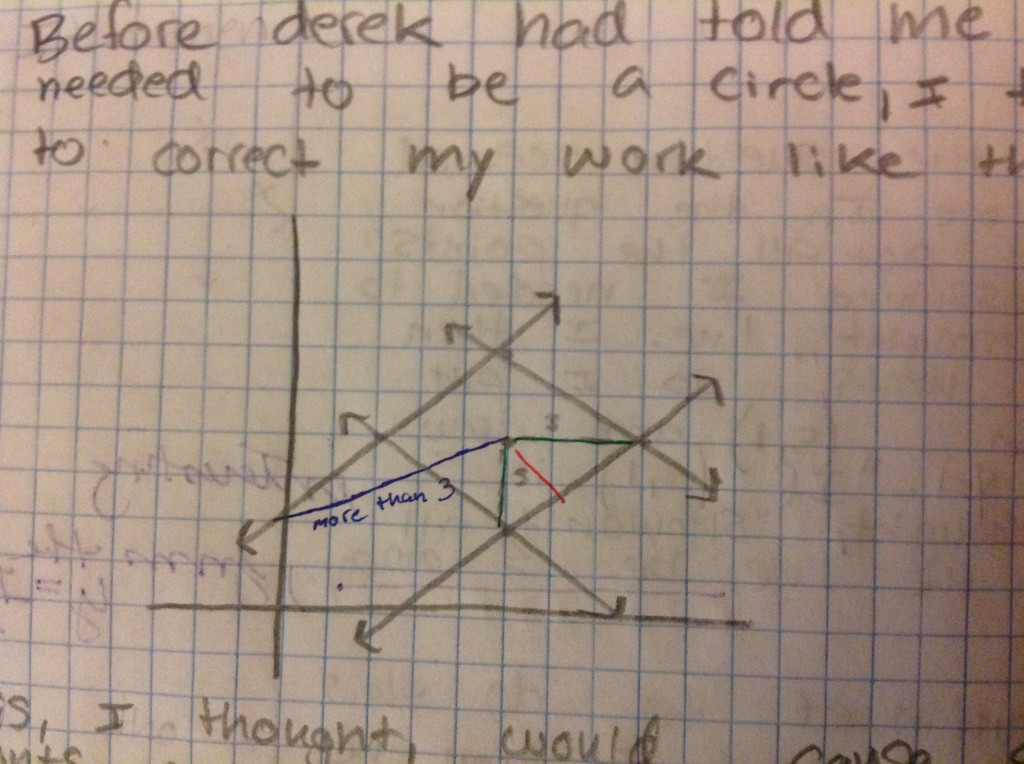
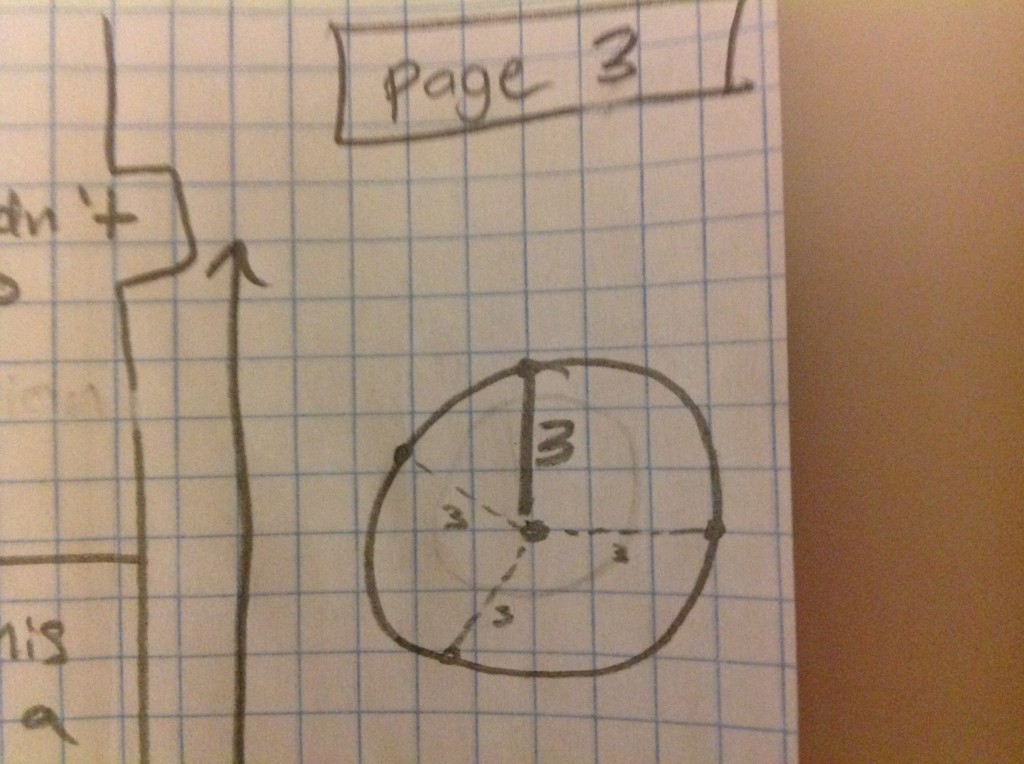
In early January, I had the good fortune to go down to the NCSSM Teaching Contemporary Mathematics Conference in Durham, NC.  There were many wonderful speakers there including Dan Teague, Maria Hernandez, Gloria Barrett and the Key Note Speaker on Saturday morning, Gail Burrill.  Gail spoke about making up tasks and lessons that actually allowed students to ask good questions that made them think mathematically.  She gave many wonderful examples and talked a lot about the responsibility of the teacher to probe and use the following pedagogical strategies:

The tasks we give and questions we pose should ensure that students:

  1.  are actively involved in choosing and evaluating strategies, considering assumptions, and receiving feedback.
  2.  encounter contrasting cases- notice new features and identify important ones.
  3. struggle with a concept before they are given a lecture
  4.  develop both conceptual understandings and procedural skills
(National Research Council, Adding it Up (2001) and How People Learn (1999) From Burrill’s Presentation)
She also gave this wonderful rubric for Inquiry Math Tasks

It made me realize that because I use a PBL curriculum very few of the problems that we look at are actually full inquiry (or student-generated). Although what happens in class is that students will create questions that I think are wonderful and a lot of discussion stems from those questions.

It will be a whole other blogpost for me to detail how problem-based learning fosters every one of those in a meaningful way.  It really blew my mind when I was sitting there listening to her.  I was thinking,”This is an amazing framework to describe to people what PBL is like.”  In fact, at one point she said that she believe that all mathematical tasks should be done where students “work alone a bit, and then they share.”  I thought that is exactly the pattern of grappling with problems for homework and then sharing ideas the next day in class.  Gail never prescribed any methods or told anyone to follow any specific guidelines, but just stated these general ideas.  It was a wonderful talk.

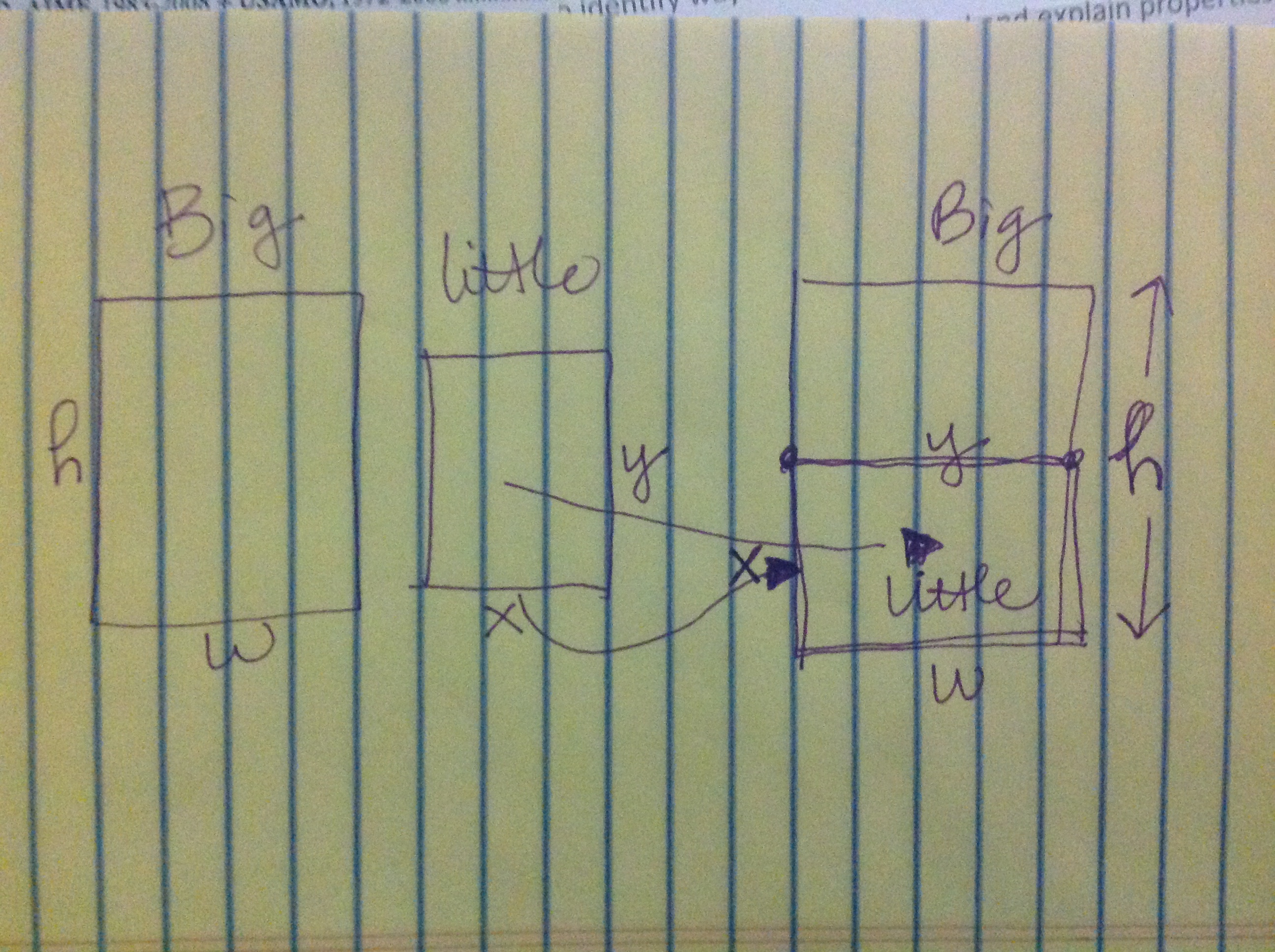
Later on that morning, I gave a talk on teaching BC Calculus with problem-based learning.  Perhaps I made a comment too many about how I was against “teaching to the test” and a young man asked a question in defense of the AP Calculus exam itself.  He felt that the multiple choice section allowed students to learn or develop intuition about questions and problem solving and that the benefits of practicing such repetitive type questions was to gain that type of intuition for those topics and those questions.  Well, I hope I am remembering this question well enough, but I would argue that intuition for problem solving and intuition for problems is two different things.  There have been many mathematicians and mathematics educators throughout time from Polya to Alan Schoenfeld who have attempted to structure problem solving or how to teach problem solving to anyone.  From my readings, there is always a “reflection” step where you compare your ideas in the “novel” problem solving process (novel being the key word here, being something that you have not yet seen).  My argument being that repeating the same type of problem definitely ensure that on a test with the same type of problems you may be able, under pressure, to answer those problems correctly.  Does it show that you have developed an intuition on what to do in those types of problems?  Perhaps.  It might show that you have differentiated between the different types of outcomes of those problems.  Does it show that you understand that concept or that you understand what the question is asking?  I am not sure.  I have worked with enough students who have mastered the art of eliminating answers in a multiple choice scenario to know that it does now show understanding, but intuition about answering the question.

However, I do think that having a student practice problem solving in a way where you are faced with a novel problem on a regular basis (perhaps nightly – along with other problems that they have seen before) where they are asked to try something new and reach into their prior knowledge and write down what they think they might be able to do allows them to practice creativity, risk-taking, connection and sharing those ideas.  After a long period of time of doing this, it would seem that some type of intuition becomes habit and they develop more knowledge about mathematics overall. More importantly, “Students are thus engaged in the creation of mathematics, allowing them to see mathematics as a part of human activity, not apart from it.”  I believe that’s why PBL in mathematics is even more important than in other disciplines and that we need to change the culture of the classroom before asking more from our teachers and students.

Using Journal Writing in PBL

1 Comment

Over the years, especially in PBL with mathematics, I have found that students greatly appreciate the authorship and ownership that comes with keeping a journal in my classroom.  In fact when I asked my students earlier this year, “When do you feel most confident in this class?” and here are some of the feedback responses they gave me:

“When I am about to hand in a journal.”
“When I am writing a journal entry because there are various concepts that initially don’t understand, and after discussions I make big discoveries and therefore it makes writing about it easier for me.”

There is something that I have come to appreciate about the way students grow to be able to show how they understand a concept.  Recently, I read a student’s journal entry and thought it was so amazing that I asked him if I could blog about it.  I thought that it really showed how he moved through his understanding of the concept and how he struggled with it to the end. In fact, he presented this problem in class thinking that he had gotten it right and wonderfully, kept going and learned something in the process.

The student – let’s call him Pete- was dealing with a problem that was towards the end of a thread that dealt with the concept of distance – distance between two points, distance between a point and a line, distance between two lines, etc.  This question was asking students to think about two different types of distance.  Here’s the problem:

“Plot all of the points that are 3 units away from the x axis and write an algebraic expression for those points.  Then plot all the points that are 3 units away from the point (5,4) and write an algebraic expression for those points.”

Up until now all we had discussed was writing expressions for Pythagorean distance between two points and writing equations for equations of lines.  We had also talked about the fact that the closest distance from a point to a line is the perpendicular distance.  So Pete was easily able to answer the first part of the question seeing that the set of all points that were 3 units away from the x axis were both the line y=3 and the line y=-3.  He drew a diagram discussing his concept of distance from a point to a line and how he visually (in his mind and physically on paper and at the board that day in class – connected them together).

However, in his journal he wrote about how the second part of the question seemed just as easy to him at first.  “I assumed I needed to do a straight line. I then saw ‘three units’, so I put a point on (5,1), and drew the line y=1.  If (5,1) was 3 away, I thought, shouldn’t all the points on the line be 3 away?” Here’s what his first diagram looked like:

Pete’s First attempt

Pete had tried to use his understanding of distance being “three units” away from a point in the same way that being “three units” away from a line in the previous problem.  However, when he was at the board, another student told him they had thought of it another way and shared with Pete something Pete realized very soon…. “Only 1 point on each of the lines was actually 3.  The rest of the points were actually all further than 3 units from the point.”  Here’s his diagram of his realization of that:

Second attempt

So now Pete is discussing how he is using his knowledge of Pythagorean distance and seeing that only the vertical and horizontal points are actually the required 3 units away.  Huh, how does he move forward now?  At the moment when he was in class, it took another classmate to say that ALL the points were supposed to be 3 units away and that he (that classmate) thought it would look more like a circle.  Pete was still determined to correct his own work (which I just love) then attempted this drawing:

 

Third attempt

Pete writes:

“This, I thought, would cause all points on the line to be 3 units away from point (5,4).  However, I was again wrong.  The blue line on the diagram shows a point on one of my lines that was more than 3 units from (5,4). The red line shows a point on one of the lines that is less than three units from (5,4) [it would’ve been great if he went into more detail, but at this point I’m so psyched that he’s going into this much detail!]  The green lines are points that are 3 units away from point (5,4).  I have effectively created a range of lengths from (5,4) opposed to what the question was asking for which was 3 units from (5,4).”

This is some of the most insightful journal writing I’ve ever seen from a high school student.  Pete is moving through his understanding of what it means for a point to be 3 units away from another point (even when another student has imposed their understanding on him) and is trying to show me how he came to understand his classmate’s argument that it is a circle.  Realizing that there are points that are more than 3 units away (farther out than this diamond shape), 3 away (at the vertices) and closer than 3 (along the sides of the diamond)….well, that there was a range and not all constantly 3, showed him that his ideas was not correct.

Pete then draws this diagram:

Getting the concept

After understanding this, Pete writes:

“It made perfect sense!…Any point from the centerpoint of a circle to any point on the circle was the same length (the radius).  I immediately drew the connection.  3 was the radius and (5,4) was the center.  the distance between the middle point and any point on the circle was 3!”

Although Pete didn’t write about the discussion that ensued about the algebraic expression, I still felt like the goals of metacognitive journaling were reached with this entry.  Pete has articulated why he chose this problem to me, he started with his misunderstanding, how another student or the class discussion/experience had helped move him through his understanding and he could clearly write about how he now has a good understanding of the mathematical concept.  I was so proud of Pete.  Yes, it’s true, not every student gets to this point of writing mathematically by January of the school year, but the growth that occurs in each individual student is what is important – not necessarily the level of maturity in the writing.  However, I have learned not to prejudge or dismiss any student who starts off at a lower level because I believe they are all capable of growth.

If you are interested in looking at my grading rubric for journals or asking me questions about how I use them in the course, don’t hesitate to get in touch. (If you are looking for the grading rubric, make sure you scroll to the third page of that pdf).

Does PBL teach Resilience?

I just read a great blogpost by a business writer, Gwen Moran, entitled, “SIx Habits of Resilient People.” When I think of people that I admire in my life for their resilience there was usually some circumstance in their life that led them to learn the quality of resilience because they had to. Even the examples that the author uses in this blogpost – being diagnosed with breast cancer, almost being murdered by a mugger, the inability to find a job – these tragedies that people have had to deal with can be turned into positive experiences by seeing them as ways in which we can learn and grow and find strength within ourselves.

But wouldn’t it be great if it didn’t take a negative experience like that to teach us how to be resilient? What if the small things that we did every day slowly taught us resilience instead of one huge experience that we had no choice but to face? Having to deal with small, undesirable circumstances on a daily basis, with the help and support of a caring learning community would be much more preferable, in my opinion, than surviving a mugging. (Not that one is more valuable than the other). But I just wonder – and I’m truly ruminating here, I have no idea – if it is possible to simulate the same type of learning experience on a slower, deeper scale by asking students to learn in a way that they might not like, that might make them uncomfortable, that asks more of them, on a regular basis.

I think you know what I’m getting at. Does PBL actually teach resilience (while also teaching so much more)? In my experience teaching with PBL the feedback I’ve received from students has been overwhelmingly positive in the end. But initially the comments are like this:

“This is so much harder.”
“Why don’t you just tell us what we need to know.”
“I need more practice of the same problems.”
“This type of learning just doesn’t work for me.”

Having students face learning in an uncomfortable atmosphere and face what is hard and unknown is difficult. Thinking for themselves and working together to find answers to problems that they pose as well as their peers pose is very different and unfamiliar. But does it teach the habits that Gwen Moran claim create resilient people? Let’s see. She claims that resilient people….

1.Build relationships – I think I can speak to this one with some expertise and say that at least if the PBL classroom is run with a relational pedagogy then it is very true that PBL teaches to build relationship. My dissertation research concluded nothing less. In discussing and sharing your ideas, it is almost impossible not to – you need relational trust and authority in order to share your knowledge with your classmates and teacher and this will only grow the more the system works for each student.

2. Reframe past hurts. – If we assume that real-life “hurts” are analogous to classroom mistakes, then I would say most definitely. PBL teaches you to reframe your mistakes. PBL is a constant cycle of attempting a problem->observing the flaw in your solution ->trying something else and starting all over again. This process of “reframing” the original method is the means by which students learn the the PBL classroom.

3. Accept failure – This may be the #1 thing that PBL teaches. I am constantly telling my students about how great it is to be wrong and make mistakes. You cannot have success without failing in this class. In fact, it is an essential part of learning. However, students in the US have been conditioned not to fail, so that reconditioning takes a very long time and is a difficult process.

4. Have multiple identities – In a traditional classroom, certain students fulfill  certain roles – there’s the class clown, the teacher’s pet, the “Hermione Grainger” who is constantly answering the teacher’s questions, etc. But what I’ve found happens in the PBL classroom is that even the student who finds him/herself always answering questions, will also find him/herself learning something from the person s/he thought didn’t know anything the next day. Those roles get broken down because the authority that once belonged only to certain people in the room has been dissolved and the assumption is that all voices have authority. All ideas are heard and discussed. PBL definitely teaches a student to have multiple identities while also teaching them a lot about themselves, and possibly humility, if done right.

5. Practice forgiveness – This might take some reinterpreting in terms of learning, but I do believe there are lessons of forgiveness in the PBL classroom. Students who expect themselves to learn everything the first time and when they don’t, feel stupid, need to forgive themselves and realize that learning is an ongoing process. Learning takes time and maybe needs more than one experience with a topic to see what the deeper meanings and understandings really are. Since PBL is not just a repetitive, rote teaching method, students need to learn how to be patient and forgiving of their own weaknesses as a learner and take time to see themselves as big picture learners.

6. Have a sense of purpose – This habit is about “big picture” purpose and looking at a plan. From the research that I did, I also found that PBL brings together many topics in mathematics, allowing students to see the “big picture” connections between topics much better than traditional teaching does. The decompartmentalization that occurs (as opposed to compartmentalizing topics into chapters in a textbook) is confusing at first because they are not used to it, but eventually students see how topics thread together. Just the other day in my geometry class we were doing a problem where they were asking to find as many points as possible that were 3 units away from (5,4) on the coordinate plane. A student in the class asked, “is this how we are going to get into circles?” The whole class was like “Oh my gosh, it is, isn’t it?” Bam, sense of purpose.

All in all, I feel that PBL meets Moran’s criteria of “resilience characteristics” in ways in which it allows students to practice these habits on a regular basis.  So not only does PBL help students learn collaboration, communication and creativity, but perhaps they will see the benefits over time in learning how to move forward from a setback – just a little.

 

Experimentation, Creativity and Problems

Returning from vacation is always a tough time, but the other day in my honors geometry class, I decided to present them with a problem that had at its heart the Pythagorean Theorem – which we’ve been using since the beginning of the year – and I wanted to see what they would do with it.  So I showed them this video I found on line.  It poses an interesting question regarding buying android tablets and what size you might want.  Before we watched it, I had them search online to compare the prices of some well-known tablet brands and see if there was a major difference in their 7 inch size tablet vs. their 10 inch size tablet.  We came up with some prices that looked like this:

We talked about how, in most cases the price of the 10 inch tablet was about 1.5 or 1.6 times the price of the 7 inch tablet.  Was that reasonable?  Did it make sense?  10:7 was only about 1.4.  So then we watched the video:

Visit NBCNews.com for breaking news, world news, and news about the economy

I posed the question to them, “Do you think what this guy is saying is true?  Is the 10 inch table really twice as big as the 7 inch? If so, what evidence can you give to say that it is and how can we justify whether or not any of these tablets really are?”

Great conversation ensued.  I was so excited.  One group of students started trying to find numbers that the dimensions of the two tablets could be.  Of course, the first thing they assumed was that the one with the 10-inch diagonal screen would have width of 6 and height of 8 (don’t we all just love those Pythagorean Triples?) but then they realized when they did that there could be so many other triangles that could have a hypotenuse that was 10 as well.

Another group started trying to compare the areas of the screens to see if they could find dimensions of two tablets that actually had one area that was twice as big as the other one (that kept the diagonals 7 and 10).  This was an interesting group because they had thought through the concept of “twice as big” but hadn’t made the jump to what it would mean for one to be that much bigger.

I was then called over to a group where a girl was trying to explain her idea of how to make two 7 inch tablets fit into the 10 inch tablet.  I’ll call her Tracy.  Tracy said something like this to me: “If ttwo small ones fit into one of the big one, that would mean that the height of the big one is twice as big as the width of the little one” and she proceeded to go up to the board and draw a picture like this:

This started everyone talking.  It actually became really cool for a while.  They soon realized that you could let the dimensions of the smaller tablet be w and 1/2h while the dimensions of the bigger one were h and w.  This combined with the Pythagorean Theorem allowed them to solve a quadratic system of equations to find the dimensions of both tablets, if it were true that the 10 inch tablet were truly “twice as big” as the 7 inch. (I believe the 10 inch tablet had to be 8.24 inches by 5.65 inches approx).

We were unable to confirm all of this by finding dimensions online so if anyone can do this, please let me know!  But what was the most amazing part of this problem solving exercise for me and my students was the engagement that I observed from their interest in the problem and their own motivation to come up with a way to justify or debunk the claim made in the video.  We are going to write up some paragraphs about their findings and present them to each other next time we meet.

I was very proud of the way they were not afraid to experiment with different ideas initially and how Tracy moved through her own ideas and took risks with the group and those around her, eventually getting her and others to the path that made sense to many of them.  It was really a group effort and worked well.  If anyone else tries this, please let me know how it goes.

Top 5 Recommended Readings for PBL Teachers Part 2

So, I finally got this done and I’ll continue with the top three readings that I just found extremely useful in my teaching last year.

3. The Innovators’ DNA: by J. Dyer, H. Gregersen and C. Christensen

I rarely recommend books that I have not read yet, but this one is actually on my list to read next so I am recommending it because everything about it just feels right to me.  Again, this is not an education book, but a book that is really for business people.  The research that was done in preparation for writing this book was looking to see what characteristics people who are viewed as transformative innovators in the business world all share.  The authors have come up with five major traits or behaviors that innovators share –

  1. associating
  2. questioning
  3. observing
  4. experimenting
  5. networking

You can read a wonderful summary of this book at this link, but I would highly recommend the book as well.  It is our job as progressive educators and teachers of PBL to teach these skills.  If it isn’t obvious to us already, as PBL teachers, I’ll say it again – that PBL is custom-made for teaching these types of skills which clearly is what this book is stating employers are now looking for.

One thing that I do not read enough of is how PBL encourages the skill of associating.  I write a lot about this in my blog and researched it in my dissertation.  In fact, connection is one of the main themes that came out in my research that students enjoyed about PBL.  The skill of associating is a major skill that is extremely important to innovation and in fact, Steve Jobs in quoted as saying, “Creativity is connecting things.”  Allowing students to practice making those connections themselves is key in order for students to practice their own creativity, especially in mathematics.

2. The Five Elements of Effective Thinking by Ed Burger and Michael Starbird

This little gem, published in 2012, was the focus of Ed Burger’s key note address at the 2012 NCTM Annual conference.  He actually didn’t try to sell the book too much, but focused on the idea of teaching effective thinking (so then, yeah, I went and bought the book – what can I say, he’s a great speaker).  As I was reading through it, all I could think about was how relevant it was to teaching mathematics with PBL.  If every student in a PBL classroom took to heart every one of the five elements that are put forth in this book, the classroom would be so much more effective (as would any classroom).

So Burger and Starbird but forth these five elements of effective thinking:

  1. Understand Deeply
  2. Make Mistakes
  3. Raise Questions
  4. Follow the Flow of Ideas
  5. Change (which they call the Quintessential Element)

So, you might ask – what’s so great about those?  I know this?  Well, it’s not those five that are so great – if you are a PBL teacher you probably are already telling your students these already.  What I think is so great about this book are the pieces of advice that Burger and Starbird give for each of these five elements.  In each chapter, these are not only examples from their own teaching but actual ways to promote each of these elements not only individually but in your classroom as well.  The anecdotes that are shared in the book are not only heart-warming but as a teacher you can see how you can make them useful in your own practice.

The combination of deliberately stating these five (and adding CHANGE as the most important) is really key for PBL.  Students may know that you want them to understand deeply and in order for them to do that they need to raise questions about their own understanding, but if you don’t constantly and deliberately create a culture for them and you in your classroom it is not a message they will receive seriously.

And the best book, that I would highly recommend reading:

  1. A New Culture of Learning, by Douglas Thomas and John Seely Brown

This book, in my opinion, is what PBL is all about.  Whether you teach in a school that uses a problem-based curriculum, uses text books and is trying projects, or if you are just trying to create a more student-centered approach to your teaching – this book is getting at the heart of what is creating a change in our schools nationwide.  It is why there is a huge movement going on with teachers in our nation trying to find something different to do in their classrooms.  Thomas and Brown describe this movement as a shift from a “teaching-centered culture” in our nation’s schools to a “learning-centered culture” which may be the most important shift in education since organized schooling began in the U.S. altogether.

This shift is based on the idea that knowledge is flexible (yes, the idea of Truth with the capital T does not exist – shhhh, don’t tell anyone).  Even in mathematics, the way that we solve problems and even the mathematics that we teach students – which topics are “most important” today- is changing rather regularly.  This has become so much more clear and visible because of not only the Internet itself, but our access to it.  Thomas and Brown suggest that we must be willing to admit that what is most important about education now is not what we teach in schools, but how students learn.  Can a student learn in the collective? Are they able to harness different modes of inquiry?  Do they experiment in their learning? This shift in the purpose of schooling is not really new to teachers but to our society it is major.  Teachers need to learn how to make this switch and articulate the deliberateness of what they are doing in their classroom in order to focus on the shift. (By the way, this also has major ramifications for teacher educators).

 I love the five dispositions that will help construct the new culture of learning (very applicable to a PBL environment!)

  1. Keep an eye on the bottom line (ultimate goal is to improve)
  2. Understand the power of diversity (strongest teams are rich mix of talents and abilities)
  3. Thrive on change (create, manage, seek out change)
  4. See learning as fun (reward is converting new knowledge into action)
  5. Live on the edge (explore radical alternatives and innovative strategies, discover insights)

All of this is so relatable to my own classroom and curriculum.  The more I create problems and experiences that allow my students do have these dispositions, the more I know that I am fostering the “culture of learning” instead of a traditional culture of “teaching.”

So that’s it.  My top 5 list of readings for PBL teachers – please let me know what you think and if you end up utilizing any of these authors’ ideas.  I know that I have been invigorated by these readings and hope that you will be as well!  Have a happy and fulfilling 2014!

Sharing in Chicago! PME-NA 2013

So tomorrow I’m off to PME-NA 2013 in Chicago which is one of my most favorite conferences for mathematics education research.  I will be presenting my research findings from my dissertation on Saturday morning and I’m so lucky to be going.  I’ve posted my PMENA handout  for anyone interested in having it.  I’m also posting  the powerpoint on my slideshare site.

Buyer Beware…when using rubrics for critical thinking skills

One of my goals in my work is often to help classroom mathematics teachers to be more deliberate in the ways in which they assess problem solving.  Although many people can be cynical about rubrics, I think that students can find them at least helpful to know what a teacher expects of them.  I have some students who told me that they pull out my rubric for grading journal writing almost every time they go to write a journal entry this fall.

However, a rubric that is vague and ambiguous about expectations can cause more harm than good.  Just throwing a rubric around that students can look at, or one that you can post on your website that you can show an administrator and say, “See, I have a rubric for that” isn’t necessarily a good thing.  Especially for problem solving.  Problem solving as a process is a very difficult thing to nail down for students especially in terms of the levels of how they can improve in their work.

I recently ran across this rubric that posted on a website under the title “Awesome Problem Solving Rubric for Teachers.”

Is this an “Awesome Rubric” for teachers?

As I read through this, at first glance the categories look pretty good – Identify the problem, identify relevant information, analyze the problem, use strategies and reflect on the process.  Sounds like a pretty standard problem solving process –very similar in many ways to Polya’s process or the steps that Jo Boaler discussed in her online course How to Learn Math this summer.

The graded level descriptors of how a student might be able to see where their work “fits” in the rubric seems to only put the behaviors on a “continuum” of Always- sometimes- never instead of trying to describe actions that the student could do that describe a mediocre way of using a strategy.    For example, analyzing a problem can be so much more descriptive than just “I think carefully” about the problem before a student starts.

They could:

1. listen deliberately to others’ ideas and reflect on them in writing or verbally

2. question the given information of a problem – does it make sense in a realistic way?

3. think about the representations they can come up with for the problem – does a graphical approach make the most sense?  Why?  Would making a geometric representation be better, if so why?

4.  In comparing a new problem to ones I’ve already done, can I list the similarities and differences?  What is this question asking that others I’ve done not asked?

How many students can really ascertain what “thinking carefully” about a problem is?  I have found that more and more we need to erase as much ambiguity as possible to help students learn to be critical thinkers.  As we feel the need to teach critical thinking, reasoning skills and sense making, it is even more imperative to have rubrics that are as precise as possible.

Now, I don’t claim that mine are perfect, but my rubrics and student feedback forms have gotten some pretty good reviews from teachers and successful feedback from students.  I work on them every summer and am continually editing in order to be more deliberate about the feedback I give my students.

I also highly recommend the rubrics from the Buck Institute Website under their “tools” category.  I also adapted one of their critical thinking rubrics that was aligned to the Common Core and changed it directly for my PBL curriculum – more for presentation of problems and novel problem solving.  I’m still working on it because I have to think about exemplars for what would be above standards, but let me know if you have any feedback.

Critical Thinking rubric for PBL

So, I would just warn anyone to beware of “awesome rubrics” for teachers that they find on the internet because something that might seem awesome at first glance might end up doing more harm than good.

30-Year-Old Wisdom, Not Recent Rhetoric

Recently, the Exeter Bulletin published an amazing Memorial Minute in honor of Rick Parris just this past week which I believe was wonderfully written.  In it they use a quote that Rick stated back in 1984 which shows his wisdom and insight into student learning of mathematics and the basis of my interest in PBL.

“My interest in such problems is due in part to the pleasure I get from working them myself, but it also stems from my belief that the only students who really learn mathematics well are the ones who develop the staying power and imagination that it takes to be problem-solvers. Such students will have thus learned that being accomplished in mathematics is not simply a matter of learning enough formulas to pass tests; that creative, original thought requires living with some questions for extended periods of time, and that academic adventure can be found in the pursuit and discovery of patterns, more so than in the mere mastery of known formulas.”

In this one paragraph is the whole of what you can find in so many blogposts, writings of so-called “experts” and “thought-leaders” in education nowadays.  I’m not so sure that the recent trend of promoting curiosity, innovation, creativity, perseverance and ‘grit’ are such original ideas.  It just has taken a long time to catch on in any type of mainstream educational jargon.

Rick Parris knew the truth over 30 years ago and led the charge in curriculum writing, pedagogical study, and leadership in student learning.  Always humble, but deeply interested in discussion, he would never shy away from the chance to discuss teaching mathematics and so I was lucky enough to have him as a colleague in the early years of my career.  He helped form my teaching philosophy and I owe a huge debt to the wisdom he imparted to me.  I seek to help students “live with some questions” every day in my classroom and I join them daily on the “academic adventure” of problem-based learning.  I can only hope that the mathematics community and society as a whole in the U.S. can catch up with his wisdom and we can eventually change the way we view learning mathematics.

Get Comfortable with Uncertainty: A Short Dialogue

And so it begins.   The students are flustered. The emails are coming at night.  The faces stare at me, scared to death.  Although I repeat numerous times, “You do not have to come to class with each problem done and correct” students are totally freaking out about the fact that they can’t “do their homework” or they can’t “get” a certain problem on the homework.  No matter how many times I attempt to send the message the first few weeks about how unnecessary it is to come to class with a problem complete or an answer to show, students feel the need.

Tomorrow I am writing on my large post-it notes in HUGE capital letters, “Get comfortable with uncertainty because it’s not going anywhere.”  Every year about this time, I give the speech about how my homework is extremely different from any homework they have probably encountered in math class.  These are not problems that you are supposed to read, recognize and repeat.  They are there to motivate your thinking, stimulate your brain and trigger prior knowledge.  In other words,  you need to be patient with yourself and truly create mathematics.

Today I met with a young woman who I thought was about to cry.  She came and said, “I can’t do this problem that was assigned for tomorrow.”  Here’s how the conversation went:

Me: Why don’t you read the problem for me?

Girl:  Find points on the line y=2 that are 13 units from the point (2,14)

Me:  Ok, so show me what you did. (she takes out her graph paper notebook and shows that she graphed the line y=2, plotted the point (2,14)).  Great, that’s a great diagram.

Girl:  But it didn’t make sense because in order for it to be 13 units away, it had to be like, diagonal.

Me: Huh, what would that look like?

Girl: (drawing on her diagram) There’d be like two of them here and here.

Me; yeah?

Girl: But it can’t be like that….

Me: yeah? Why not?

Girl: Um…cause it wouldn’t be a straight distance.  I think..

Me: Is it 13 units away from (2,14)?

Girl: yeah, I think so…

Me: Hmmm….how far is (2,14) from the line y=2?

Girl:  Oh that’s easier – it’s like 12. ..Oh My gosh..it’s like a hypotenuse….and the other side that I don’t know is like the a and the 12 is like the b.  I can just find it.  Oh my gosh that’s so easy.  And the other one is on the other side.    Why didn’t I see that?

Me:  Well, you did…actually….

Girl: well, after you asked me that question…

Me: yeah, but eventually you’ll learn how to ask yourself those questions.

 

And they do….it’s just the beginning of the year.  We have to give them time – time to look into their prior knowledge as a habit, time to surprise themselves, time to have those moments, time to enjoy the moment and revel in the joy and courage and disappointment.  It’s all a part of the breakthrough that is needed to realize that they are creative and mathematics needs them to be.  It’s amazing and it’s worth it.

A New Year…Now What Do You Do?

OK, Carmel, enough with the summer of blogging about all this theory and ideas about teaching.  School is starting, we’ve committed to teaching with PBL – ack, things are starting to come into focus, huh?  I’m getting all these emails with questions about writing journals and dealing with parents and how to put things into action.  I’m right there with you guys….it’s Saturday and I’m having a workshop with two of my colleagues who have dedicated their time this year to teaching Geometry with me and PBL for the first time.  I’m so excited!

So I’ve put together a few documents that I think might be helpful.  The first one I’m posting here: Advice for Students Transitioning to PBL

This document is a list of quotes from actual students from years of teaching with PBL.  You can give it out if you like – maybe not on the first day, but after a few weeks – once your kids can relate.  I had kids at the end of the year write down advice to students at the beginning of the year, so that they would know how they will eventually feel.  That in the end, they will know that it’s worth it.  It’s actually kind of helpful for students to know that all of their hard work pays off.

The second document I also have posted under Metacognitive Journaling – it is a sheet that I give out about journaling and explains my expectations to students.  If you are considering assigning journals and having students use journals, this might be a good place to start for you.Keeping a Journal for Math Class

I also have written up a sheet that I call Teacher Cheat Sheet on PBL which includes some talking points for you to use when (maybe I should say “if”) you get resistance from parents.  I believe I also have an old blogpost about talking to parents too.  The initial first few months of using PBL is often very difficult, especially if your school had a traditional curriculum.  Please feel free to contact me for advice or feedback.  Honestly, what I have found most helpful is a very supportive administration and department chair and allowing parents to come and observe classes.  Don’t be nervous, because once they see that real mathematics is going on in the classroom, they become more confident in the learning.  Of course, the teachers need to feel confident in the learning process themselves before you allow the observations, but once they feel the culture of the classroom has meshed it should be fine.

Please feel free to get in touch if you have questions during this transition period and also remember that I do school visits.  Have a great beginning of the year!