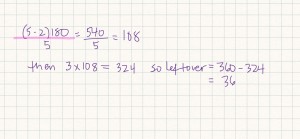Category: Problem based learning

The First Followers…how do I get them in the PBL classroom?

2 Comments

So I have one class this year that is rather frustrating and pretty tough to handle when it comes to buy-in with what I’m doing in the mathematics classroom.  Perhaps it’s because it’s first period, or perhaps it’s the mix of kids (quiet, shy, cynical?) – but I’m having a hard time inspiring them to speak out about their ideas or even be somewhat active in class.  This has made me wonder if I’m doing anything differently?  What’s the difference between first period and second period?  Why would this class be that much different in student make-up and personality than other challenging classes that I’ve had.

These thoughts made me remember a video I saw at a conference talk this summer and how important the “first followers” are.  This video is basically about a guy the narrator calls the “lone nut” who is dancing at a music festival (maybe you’ve seen it, it’s been around for a while) and how his leading becomes a “movement.”

It’s one of my favorites and so true.  But what I am afraid of is that the “first followers” I had in my first period class are not necessarily “followers” but students who realized they better do what I want or they won’t do well in my class.  This is not the same as “buy-in” to PBL.  This led me to think about what I needed to do in order to create first followers who would truly be inspiring and lead to more followers.  I’m not sure about this, but a couple things I tried:

  • talking about the pedagogy and how it’s different with the students
  • discussing the class contribution rubric with them and having them do a self-evaluation of their contributions to class
  • discussing listening skills when learning
  • Being deliberate about asking questions that are more open-ended (not just procedural)
  • Being less “forgiving” that it’s first period and they are tired – keeping my standards up of what I expect from them.
  • Giving praise when students take risks and learn from mistakes at the board
  • Offering a reward (like a Pez Candy) when a student is wrong but has taken a risk

So far my attempts have not been in vain, but I still don’t feel the “movement” as I do in other classes.  This has been an interesting first month with this group and I think many of them are actually learning, but don’t seem to be enjoying themselves.  I think I just need a couple more “first followers” to allow the others to see that what I am asking of them – although harder and requiring more energy and effort on their part – is actually an important part of their journey of learning.  I would love to hear from anyone who has experienced this and what steps can be taken to increase the followers in a “mob” of the whole class!

Blog Challenge Day 3: Do I really practice what I preach?

So the question for today is “Discuss one observation “area” that you would like to improve upon for your teacher evaluation.”  This is a tough one for me because as a teacher at an independent school formal evaluations are done in the second and sixth years so I don’t have formal evaluation “areas” per se.  Last year, I had a colleague sit in on my classes and give me feedback over a month’s period  and it was extremely helpful to have his perspective.  I also have many teachers come from other school at different points in the year in order to learn about problem-based learning, so I am used to having people in my classroom, but I haven’t really asked for feedback in one particular area in very long time.

However, I do believe that something I wonder about when I speak to teachers learning about PBL is how well I really facilitate PBL discussions.  I know what I’m supposed to do but the time constraints and the issues of adolescent life often keep me from being the best I can be.   I know I can be hard on myself, but if I had an expert in questioning, wait time, reactions to statements, inquiry and scaffolding who could come in and watch me teach for a week or so, that would probably be the best thing for me right now.  It would be so helpful.  So if anyone is willing…please get in touch!

Six of one, half a dozen of the other…I think not

2 Comments

(Sorry, this is a long one! and caveat: I am not claiming that Wikipedia is the be all and end of definitions!)

So according to Wikipedia, PBL means two things (well, three if you count Premier Basketball League, but that’s neither here nor there). If you look up PBL on Wikipedia, the first hit is, in fact, Problem-Based Learning. Why, you may ask? I believe that this is because Problem-Based Learning has been around in various forms longer than Project-Based Learning, but the term itself was coined in the 1960s by Howard Barrows at McMaster University in Ontario, Canada ( http://en.m.wikipedia.org/wiki/Problem-based_learning). You can read more about Barrows’ specific definition of Problem-Based Learning at this site and in my tab at the top of my website that says “Problem-Based Learning.” However, what I feel is one of the biggest parts of Barrows’ definition is the fact that “the problem is a vehicle for the development of problem solving skills” – that is it, that it is the problem – hopefully well developed and set in a context that is interesting, challenging and meaningful to students – through which the students will development and learn the problem solving skills.

Wikipedia names Project-Based Learning (http://en.m.wikipedia.org/wiki/Project-Based Learning) almost the same thing, however, they connect it more to Greeno’s theory of situated learning – “learning by doing” and “teaching by engaging students in investigation.” However, all of these theorists ideas range from about 1991-2006, so it would seem that a PBL by any other name…is not really the same?

One of the most important distinctions in Project-Based Learning (which I will write as PjBL, because you know, it came 2nd, for the record) is the authenticity of the task that is motivated by a larger “driving question” – students learn by creating a project and investigating what they need to do in order to organize or structure their presentation for the project.

So what does this mean in mathematics? A few weeks ago, there was quite a discussion going down on Twitter about what constituted Problem-Based Learning.

image

image

image

Dan Meyer seemed to be criticizing Problem-Based Learning saying that it was discussed by others as “too much curriculum and too little time for PrBL” and he says that he saw “a lot of fluff in PrBL” – to which I would say, there’s much more to Problem-Based Learning than just doing problems, Mr. Meyer. Nat Banting also asked for a clarification of what the difference was between a project and a problem in math education.

In response to this discussion and Mr. Banting’s question, I posted an image of a table I created listing differences that I saw between project- and problem-based learning in mathematics education and had hoped for some feedback.

image

Then I thought that maybe my description on the image of the differences wasn’t clear enough, so I thought I’d try one more time to make the distinction between the authenticity clear.

If we revisit the idea that Problem-Based Learning has at its core, problems as the vehicle for learning and constructing knowledge, I think this is at the heart of the difference of the learning/teaching experience. When I look at purposefully scaffolded and written curriculum for problem-based learning, yes there are outcomes that need to be met, there are topics that are discussed that are set by the teacher (or curriculum writer). Mathematics has within it many very interesting abstract concepts that are worthwhile to teach even though the “real-life” applications don’t have much context for students (will a student appreciate the logic and problem solving skills that are learned in factoring a polynomial, for example, or do they just accept and take it as a skill they need, or use technology and not use that part of their brain – who knows?) The point I’m trying to make is that in problem-based learning the problems would lead students to figuring out (through discussion and with prior knowledge and experience) the skills needed to create a process of factoring and perhaps “unfactoring” an algebraic expression and hopefully what that expression might represent. This is what’s known as “preauthentication” – when the curriculum writers or teachers try to come up with some kind of experience for the students that simulates the mathematicians authentic experience or “ah-ha” moment of understanding or realization. Then there are other problems that allow the students to dig deeper and apply those ideas to other areas of mathematics, and yes, real-life problems too.

In Project-Based Learning, “emergent authenticity” allows the mathematics to emerge from the ideas of the project (or driving question at hand) which is up to the students to then find out what they need to know. This is where Project-Based Learning can fall short in the area of secondary mathematics – in a world of standards. Where does the learning take place and how does it happen? Once students understand a concept, having gone through rather traditional instruction and some type of formative assessment, the project can then be given. Yes, Mr. Meyer, I believe that there is a hard balance to make there between traditional instruction and when to do the projects – quite a dilemma of time (although schools do it with very nice interdisciplinary time schedules).

However, I do believe that in problem-based learning the rigor, content, problem-solving and all the other “4C’s” skills that project-based learning also promote end up happening in the discussion and presentation of problem ideas and solutions. So I would have to argue with those who say “it doesn’t matter what you call it” and “they’re all the same thing” because the learning process in mathematics is so very different in these two methods. Hopefully, I can shed some light on the differences between PBL and what I hope will be called PjBL soon!

Keeping the Dice Rolling: Questioning in PBL

Returning from a week-long conference is always invigorating for me – not for the reasons that many people think.  I do appreciate the great feedback I get from my “teacher-students” that I interact with during the week who are so extremely eager to learn about PBL – this truly invigorates me and allows me to do so much work over the summer myself.  However, what I always look forward to is how much I personally learn from the interactions with my students that week.  At this point, PBL is so popular in its use in mathematics classrooms across the country, although people see me as an expert in the field, I gain so much from the questions and process of those who are learning that it is so useful for me to move through that process with them all the time.  I believe this is why they call it “professional development”!  So I just wanted to give a HUGE shout-out of thanks to everyone who took my workshops, came to my Cwic sessions, had conversations with me or interacted in some way – it might have been one of the best professional weeks I’ve ever had!

Since that week in New Hampshire, I’ve done a lot of reading, editing of my own materials, and catching up with my own work.  I recently read a blogpost on edutopia entitled “The Importance of Asking Questions to Promote Higher-Order Competencies” which stood out to me as something that we talked a great deal about in my own PBL classes, although this blogpost was not specifically about PBL or math at all.  It was written by a professor at Rutgers University in the Psychology Department, Maurice Elias, who is part of the Rutgers Social-Emotional Learning Lab, and made me wonder if he had done any work with Cindy Hmelo-Silver, who is also at Rutgers and does work with PBL in Psychology.  The concept of asking questions is something that we discuss and practice in my workshops because Hmelo-Silver says that it is a characteristic of an experienced PBL teacher to ask probing questions that are metacognitive and at a higher-order level.  Interestingly, the four areas that Elias discuss are often not linked to higher-order thinking (for example, yes/no questions) so I thought I might take his “Goldilocks” example and try it through the lens of math PBL.  Elias’ four questioning techniques are 1)Suggest 2) Ask a Closed Question 3)Ask an open question and 4)The Two Question Rule.

The idea of “suggestion” is one that I always tried to stay away from since student voice and experience is first and foremost in my mind as a pillar of the PBL pedagogy.  Allowing students to make first attempts at making those connections on their own I believe takes precedence over critical thinking skills of choosing from alternatives.  However, that concept of making a choice between alternatives is important as well and might be a very good skill to have them practice every now and then deliberately.  I think I will begin to try this in class.  The next time when it seems like no one has an idea or when the student at the board is going in the wrong direction, I may decide to say something like “Should Joe go with the method of completing the square or factoring here?”

The second idea of asking the closed question (yes or no) is also one that I have always tried to stay away from.  In my experience it’s kind of a conversation staller, but the way it’s explained by Elias in his blogpost is actually a very interesting twist on the closed question.  It takes a yes or no question but embeds an opinion in it, so almost forces a justification of the closed question with the yes or no.  It makes the teacher find a way for the student to continue (well, the teacher must make sure the student follows up).  So for example, if the teacher asks asks, “Do you think the quadrilateral is a rhombus?” it might seem very obvious that a student could just say yes or no and the conversation could just end there.  Everything I’ve read about closed questions say that you should not phrase the question that way but be sure that the question has within it some interest in the student’s opinion. “Why do you think it’s a good idea to argue that this quadrilateral is a rhombus?” (Which is a closed question in disguise but opens up the conversation).

Then there’s the Open-Ended Question (or what Bingham calls a True Question) which I have written about before.  I talk about this in my workshops as well and real open-ended questions are questions that the teacher doesn’t really know the answer to.  I love Bingham’s analogy of trying to predict with your students what the sum of two dice will be (the answer)  but trying to keep the dice rolling for as long as possible without knowing the answer.

Dice Metaphor

What’s an example of this type of question in mathematics?  This is a tough one because as we know so well, there are definitely right and wrong answers in mathematics.  However, we can ask questions like “Why did you chose that method?” and “What do you think of Sara’s argument? Do you agree with her?” These types of questions can make mathematics teachers very uncomfortable but we can keep the box wiggling for great deal longer than we could before with these questions and they allow us to work towards the CCSS Mathematics Practice Standards of persevering and critiquing other students’ work.

Elias’ Two Question Rule isn’t just as simple as asking a follow-up question, but makes the assumption that students want to see if when you ask a question the first time, you really wanted to know what they wanted to say.  For example, in most mathematics classrooms, students are accustomed to the I-R-E form of dialogue which is short for Initiation-Response-Evaluation (Teacher-Student-Teacher) where the teacher generally knows that answer that they want for the question they have asked (kids know this, they’re not dumb).  So when the same old kids do the response part of this, instead of just doing the evaluation part, why not blindside them and actually rephrase the question and ask it again in a different way, or ask one kid themselves individually in order for them to know that you really want to hear from them?  I think that’s what Elias is talking about.  (or even better don’t use IRE, break that darn habit, I know I’m still trying to!)

We had some great fun during my workshops role modeling and just trying out different ways of questioning the mock student who was at the board – it’s hard to break old habits.  But the more we are aware of what we are trying to do and do it deliberately, the more important it becomes and bigger agents of change we can be as well. If you have any thoughts on these questioning techniques in math PBL classroom – please let me know

Hmelo-Silver & Barrows (2006). Goals and strategies of a PBL Facilitator. Interdisciplinary Journal of Problem-Based Learning , 1(1), 21-39

Looking for the Teacher of Grit

I’m in the middle of working on organizing my courses for the Exeter conference in about a week and something I’m really struggling with is trying to articulate to teachers how they can impart to their students this idea of grit in the PBL classroom.  So I started doing a little research online (besides looking through all of the books I have read on the subject).  I took Angela Duckworth’s Grit Test at her lab’s website (got a 3.63 grit score- grittier than 60% of other U.S. citizen’s my age…hmmm).  Then I started reading some blog posts of other PBL teachers and writers like here on the MAA’s blog which is trying to encourage math students to tinker with problems or here which is more of an all-purpose index of resources to teaching grit. There was this wonderful video of a teacher in NH who created a neat grit curriculum for her 5th grade class (with Angela Duckworth too)

John Larmer of the Buck Institute wrote a really nice blog entry on how project-based learning fosters grit in students. I even found a nice video of Po Bronson, author of Nurture Shock (the book about how parents have failed kids because we don’t let them fail).  This is a short video of how Mr. Bronson believes we should be allowing kids to fail these days.

He says (in so many words) that if kids grow up without learning how to fail, they will become risk-averse.  This is what I am finding in my classroom at times.  The risk-averse kid combined with the fixed mindset kid, combined with the “I-have-to-get-into-college-and-make-my-parents-happy” kid makes the PBL classroom very difficult when you are trying to get them to take risks and be creative.  Add that to the classroom culture that they have been used to for the first 9 years of their education in the U.S. and sadly, it makes for a tough place to foster the teaching of grit.

In fact, on my most recent course evaluations I asked students what they found most challenging about the class and the two pieces that tied for first place were journal writing and

“having to be vulnerable and make mistakes in front of my peers.”

I so want to change that and I always thought that I created a classroom atmosphere where students were comfortable.  I did all of these things that the professionals are suggesting on these websites:

1. modeling risk-taking and making mistakes myself
2. talking about growth mindset regularly
3. ask them to write about positive experiences when they are proud of themselves
4. using class contribution feedback forms (self-report and analysis of class contribution sheets)
5. using strategies where students think of a wrong way before we talk about the correct solution method together.

But somehow, even at the end of the year, their fear of being wrong in front of each other (and me, some commented) is still predominantly what they say challenged them.  So I would say to Po Bronson, where is the teacher of Grit?  What is the secret?  How do I make it so?  Is there a time when it’s too late for some kids?  Most of what I’ve seen on the internet is teaching grit to elementary school children – does the fact that I am teaching high school kids make it any harder?

I finally found this great Prezi created by a teacher named Kristen Goulet which, I know, is geared towards elementary school kids, but I think I could find a way to direct it towards older students.  The idea of having them ask themselves whether their self-talk is “because of me” or “because of other” and whether it is “permanent (i.e. fixed mindset)” or “temporary (i.e. growth mindset)” definitely would help them realize how much of the way the deal with adversity is flexible.  It also helps with seeing how to have a more realistic and optimistic view of a certain situation (and is kind of hard to argue with).

So, I’m still in search for the best practices to teach grit (and apparently so is Angela Duckworth – she admits this in her TED talk), but now I know that it is way more complex than just following a certain number of steps – it has so much more to do with a student’s socio-emotional state of mind. Vicki Zakrzewski’s article “What’s wrong with Grit?” is probably the closest I got to agreeing with someone’s assessment of grit and how to teach it.  I know that I am really good at letting kids know what is important to me and doing that modeling that is important as well.  Undoing what has happened to them before they got to me is a tall order, but I’m not going to stop trying.

Finding Inspiration In All Sorts of Places

“Kids will never understand fully if you just tell them the answer.  They have to break it down and understand it, take it piece by piece ‘cause if you get it straight on you’ll never know what happened. Like if you’re building something you’ll never understand how it’s built, you can never build it again because you don’t know what to do.”

You might think this quote comes from an experienced teacher who has worked with many students over years of seeing how they learn best.  Someone who has found that over time best practices have shown that individuals must spend time with material and grapple with their own understanding in order to learn for understanding.  However, this weekend I heard a fifth grade student named Jessica say this very quote in a video.  Words of wisdom from this young student who has experienced learning in a way that has been very meaningful to her.  Another teacher puts it this way:

“We’re asking students to do things that, at first, may be a little beyond them. But because of the way we present it, they find that they can do it. They’re not finding out how to do it by listening to the teacher explain.  They’re experiencing themselves as people who are capable of learning increasingly difficult skills. Confidence comes from knowing that “I can do it!” – Ted Swartz, Ph.D.

This may be the most controversial part of my definition of PBL.  The concept that not only the students are learning through their own inquiry and curiosity, but that they are asked to apply their own prior knowledge and to do so at an increasingly difficult rate of skills.  That they are asked to challenge themselves again and again.  Another big difference is the way that students experience themselves.  Swartz states that students experience themselves as learners who are capable of so much more than just listening to a teacher and doing what someone external to themselves tells them to do.  They are capable of their own direction in learning and of learning increasingly difficult tasks and managing those.

Also, students in these types of classrooms are concurrently practicing and learning new skills.  This is very different from the way we all learned as children and adolescents and it also goes against the culture of the math classroom in most of the U.S. today so we must set new norms and explain this to parents.  But it is something that is very rewarding.

We just had our Parents’ Weekend at my school and the two new teachers who were working on our pilot PBL shared with me stories of parents who had had negative feelings towards the curriculum at the beginning of the year.  I was nervous about how they were responding now, at the end of the school year.  However, to my surprise, my colleagues shared with me stories of how proud of these parents were of their students presenting in front of the class and articulating mathematical concepts to their classmates very well.  Are these straight A students now?  Not at all, but they are proud of their work, engaged in the discussion and enjoying math class.  These are great strides for these students.  And at the end of year where we worked very hard, this was truly inspirational.

PBL at NCTM 2014!

One of my major goals in attending the NCTM annual conference this year was to see how widespread PBL had become in terms of mainstream education practices across the US.  I have to say that this year there were quite a few sessions that had PBL in the title or as the central theme and I was excited to see that!  Here were some of the workshops:

Problem-Based Learning (PBL) Is More Than Solving Problems – in this session the speakers were giving just a beginner’s view of what PBL is and can be in the classroom.

Change the Classroom, Not the Students – Attaining Equity Using PBL (OK, this one was mine)

Bring Back Problem-Based Learning into Methods Courses! – in this session the speaker makes an argument for using PBL methods in courses for teacher candidates and spoke about the positive experiences of preservice teachers with PBL.

Amplify the Mathematical Practices -this session focused on middle school PBL practices and how they stressed the CCSS MP standards.  This was sponsored by Amplify’s Math projects.

Making Mathematics Culturally Relevant to Students Using Problem-Based Learning – in this session, the speakers gave an example of culturally relevant pedagogy striving for equity in the classroom.  Again arguing that PBL allows for furthering equity in the practice of PBL.

Setting the Scene: Designing Your Problem-Based Classroom – in this session, the great Geoff Krall (emergentmath.com) gave a great talk summarizing a lot of his methods relating to PBL and his protocols in getting students to work through problems in their learning.

The Hidden Message: Micromessaging and Mathematics – I wanted to attend this session so badly, but I had to leave early on Saturday morning.  This session has so much to do with my own research relating to how we talk to each other in mathematics classrooms and how PBL can allow for better communication without the micromessages.  (Tujuana if you read this – get in touch with me!)

Promoting Equity through Teaching for a Growth Mindset (Jo Boaler) – in this Session Prof. Boaler reported on her work in math education with Carol Dweck’s Mindset research.  You should check out her new website youcubed.org if you are interested in all the resources that she has shared freely.

And that was just to name a few!  So much wonderful information out there to learn and share.  The variety and number of sessions that connected to the pedagogy, content or philosophy of PBL was overwhelming and honestly very invigorating for me as someone who has taught with PBL for over 20 years.  Seeing the interest and enthusiasm for this type of classroom practice has given me renewed energy to get me through the rest of the year!

Handouts – Front and Center

I always try to make it easy for people to find both my slides and handouts when I give a talk – so Here’s my powerpoint presentation from my talk entitled, “Change the Classroom, Not the Students: Creating Equity with PBL”  which I’m giving today at the NCTM Annual Conference in New Orleans – great to be here.  I also have 2 handouts which include my framework for a relational PBL class and the results of my qualitative dissertation – I’d love to hear any comments and questions and start a discussion with PBL teachers. (I do not include the videos I used in this public version of the powerpoint, sorry)

[slideshare id=33364598&doc=changetheclassroomschettino-140410070229-phpapp02]

Schettino Framework Handout

Schettino Sample Problems Handout NCTM2014

There are actually a few talks here today that I would highly recommend and seem to be related to this topic of creating a classroom that allows for discussion and interaction at the level of creating equity.  One of them is on Friday, and is entitled “The Hidden Message: Micromessaging and Mathematics” and it seems to be about managing the way we talk to each other in the classroom and making sure all voices are heard.  I’m definitely going to that one!  Unfortunately, Jo Boaler is presenting at the exact same time as me!  I don’t know if I should take that as a compliment that I was put as the same time or not 🙁

Well, hope everyone has a great time!  Enjoy the conference!

PBL & James and the Giant Peach: Try looking at it a different way

2 Comments

James Henry Trotter: “When I had a problem, my mum and dad would tell me to look at it another way.” (Roald Dahl)

I’ve always thought that PBL fostered creative problem solving as opposed to memorization of pneumonic devices.  One of my students today proved me right when I gave a “quick quiz” on the use of the idea of tangent.  We had discussed tangent in class for only two days and in two ways – one as a slope of a line with a given angle and from that idea we discussed how it could be interpreted as the ratio of the sides of a right triangle (if you put a right triangle under the line).

Of course, during this conversation some student who had studies the ever popular SOHCAHTOA before mentioned this in class and told everyone that they had just memorized this and that’s how they knew it.  I said that’s fine but I’d like them to try to think about the context of the problems and see if this helps make any sense of it for them.

So today on the quiz one student was attempting this problem – very basic, very procedural, not at all something that I would call atypical of a textbook-like problem on tangent.

A bird is sitting on top of the Main School Building and looks down at the end of the baseball field with an angle of depression of 4 degrees.  If the MSB is 87 feet tall, how far away is the end of the baseball field?

So the student attempts to create a ratio with the sides of the triangle and even sets it up correctly.  However, because she does the algebra incorrectly, she gets an answer that is extremely small 8.037 x 10^-4.  In fact, during the quiz, she calls me over and asks what it means, she doesn’t remember scientific notation and starts getting all anxious because we didn’t do anything like this in the problems in the previous two days?  How can the answer be that small?  I said well, you better go back and think of something else.

In most classes, a student in this situation might stress out, try to do the problem over again with the limited perspective of “TOA” or of just viewing the right triangle in one way.  However, because this students had also learned other students’ perspectives of tangent as slope of a line what this girl did at this point was to see it from a different way.  Interestingly, this is what she did.  In an alternative, albeit confusing way of writing the equation of the x-axis, she wrote y=0x to represent the ground.  Then she found the tangent of 4 degrees and used that as the slope of a line.  She put the bird at the point (0,87)

She writes the equation y= – (tan4)x + 87 and explains that this is the equation of a line that makes a 4 degree angle with the x axis and has a y-intercept of 87.  Then she realizes that if she finds the intersection of that line and the x-axis, she would find how far the building is from the baseball field.  This is what she does and uses her graphing calculator to get the right answer.

When she hands in this quiz to me, I half expected that tiny little answer as her distance to the baseball field.  But what I got was an amazingly inventive solution and a correct answer.  With a problem that didn’t make sense, she looked at it a different way and ended up getting the right answer.  It was amazing what changing your perspective could do and this was great evidence that even under pressure, the habits of creativity and connection were paying off.

Encouraging Student Voice without Knowing It

I’d like to think of myself as a master teacher.  I’ve always thought of myself as very aware of student perspectives in my classroom, but today after a weekend of being in bed with a bad cold, all I wanted to do was get through the problems and get back home – I admit it.  I was not being very reflective and deliberate in my teaching.  However, even with all that, something amazing happened today.  Of course, I’d like to take all the credit, but I have to say I think the credit goes to the method of PBL, relational pedagogy and the students in my class.  So here’s what happened.

We had gone through about half the problems and I think they could tell I was in a pretty bad mood.  We got to one of my favorite geometry problems that starts an interesting strand of thinking that has to do with which polygons tessellate with others.  One girl goes to the board (I’ll call her Robin) and she presents her solution to this problem:

The diagram at the right shows three regular pentagons that share a common vertex at P.  The three pentagons do not quite surround P.  Find the size of the uncovered acute angle at P.

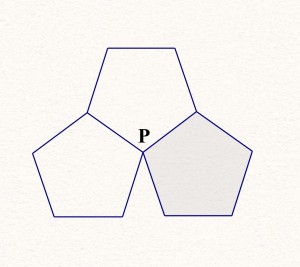
So Robin does what I expect (and in my fuzzy state of mind I am just happy that someone knows what’s going on).  She writes on the board:

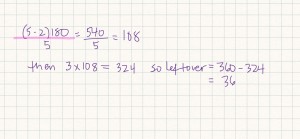
Her argument being that the three angles in the pentagons were congruent since they were all regular and the leftover part would be the difference between those three and 360.  So, I was ready to move on.  She was right, after all?  Let’s go and do the next problem.  But no, Tye speaks up and says, “Hey that’s what I got but that’s not what I did.  That’s so cool I got the right answer.”  So, as tired and sick as I was, I said, “What did you do Tye?”  He says all I did was do 108 divided by 3 and it worked!”  He was so proud of himself.  I sat there and was like, OK, this isn’t going to fly, but I was so exhausted that ….but wait, another student says, “Hey that’s cool.  You just take the angle measure and divide it by how many polygons you have.” I’m thinking, oh no, this is gonna get out of hand fast….

Then another student says, “wait a minute, lets see if it works with hexagons: ”  So before they  know it they realize that it can’t work with hexagons and Helen says, “but that’s because there are too many, you need something with room left over, like a square.  What if you only use 3 squares? Is the angle leftover 90 divided by 3?”

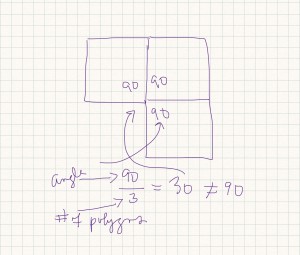
So they soon have disproved the theory that if they just take the number of interior angle of the regular polygon and divide by how many polygons there are and divide them, they’ll get the leftover angle.  But Tye is still adamant that he’s all proud he got the right answer.  I am, however, still struggling with the fact that he can’t justify to himself why it works.  I say,”Listen, why don’t you think about it some more and we’ll come back to it?” but guess what, they don’t let it go.

Luke says, “Well, what I did was just draw a triangle down there.”

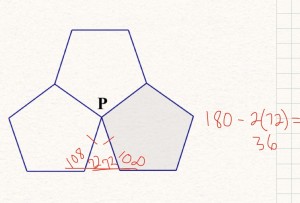
He says that he knew that empty space was really an Isosceles triangle and because the base angles were supplementary to the interior angles of the pentagon, he could find the angle at the top.  At this point, I’m like “will this ever end? Will I be able to get some Tylenol?” (I know can you believe me?  what a role model…)  A few other kids really liked what Luke did and said they did that too and thought they had been wrong, but now see that it was a valid method.  I mean, could I ask for more?  This was awesome stuff going on!

So at this point, we move on and do a few more problems, but then towards the end of class, I notice there are about three kids who aren’t really paying attention to the problem at hand.  I couldn’t figure out what was going on because they are usually right in the thick of our discussions.  So finally, one girls practically yells (and I mean, with arms flailing and everything) “I got it!”  Alanna had been working on a justification for Tye’s idea of dividing the interior angle by three the whole class period, as had two other students.  It was so interesting a problem to them that they just couldn’t stop.  Alanna said, “I knew they were vertical angles, but I just couldn’t see how they could be the same.”  She and the two other students had been playing with some isosceles triangles and vertical angles and come up with this solution:

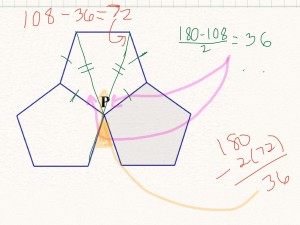
By finding that the base angles of the isosceles triangles on the sides were both 36, and that the one in the middle was also 36, they had seen the reason why Tye could just divide 108 by 3.  They knew it wasn’t just pure luck that it worked and it made them all so happy.  It was so satisfying and I could just feel the excitement in the room.

It was so funny to me because everything that I did to try to discourage them from going to that place of curiosity or demanding the reason didn’t help.  They went there anyway. Their voices were heard – again and again.  The culture that we had set was there and no matter what I did now, at this point in the year, they knew what was expected of them – asking questions, not giving up, being inquisitive & creative.  This class helped me realize that even on my bad days I need to see each student for who they are and be just as excited for each of them to realize their own potential.  And if I don’t have the energy or strength to push them through, maybe, just maybe, they will.