Category: Problem based learning

Why Teachers Don’t Give Feedback instead of Grades, and Why We Should

7 Comments

First in a series of posts about my experiences with “Feedback Before Grades”

Holy Mackerel is all I have to say – Ok, well, no I have plenty more to say – but after about a week and a half of holing myself up with my colleague, Kristen McVaugh, (big shout-out to Ms McVaugh who is not only teaching PBL for the first time but was willing to dive into this amazing journey of alternative assessment with me this year too), I am totally exhausted, almost blind as a bat, partially jaded and crazy – but mostly ready for a drink.  This little looped video of Nathaniel Rateliff and the Night Sweats pretty much sums it up…

So here was our well-intentioned plan:  we wanted to start the year off with a different type of assessment.  I put out my feelers on twitter and asked around if anyone had a rubric for grading assessments where the teacher first gave only feedback and then allowed students to do revisions and then once the revisions were done the students received a grade. Kristen and I knew a few things:

  1. we wanted to make sure the revisions were done in class
  2. we wanted to make sure the revisions were the students’ own work (tough one)
  3. we wanted to give students feedback that they needed to interpret as helpful so that we weren’t giving them the answer – so that it was still assessing their knowledge the second time around
  4. we wanted to make sure that students were actually learning during the assessment
  5. we wanted students to view the assessment as a learning experience
  6. we wanted students to be rewarded for both conceptual knowledge and their skills in the problem solving too

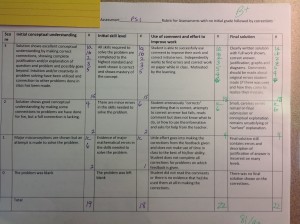
So we created this rubric Initial Draft of Rubric for Grading.  It allowed us to look at the initial conceptual understanding the student came to the problem set with and also the initial skill level. Kristen and I spent hours and hours writing feedback on the students’ papers regarding their errors, good work and what revisions needed to be done in a back-handed sort of way.

Here are some examples:

Student 1 Initial Work
Student 2s initial work
Student 3 initial work

 

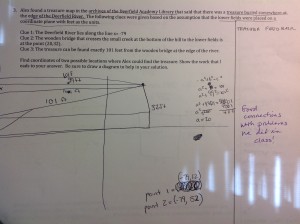
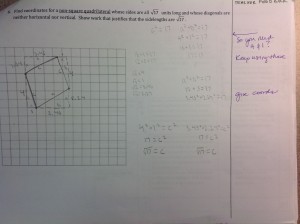
Some kids’ work warranted more writing and some warranted less.  Of course if it was wonderful we just wrote something like, excellent work and perhaps wrote and extension question.  The hard part was filling out the rubric.  So for example, I’ll take Student 3’s work on problem 6 which is the last one above. Here is the rubric filled out for him:

Student 3’s Rubric

You will notice that I put problem 6 as a 1 for conceptual understanding and a 2 for skill level (in purple). In this problem students were asked to find a non-square quadrilateral with side lengths of sqrt(17).  Student 3 was definitely able to find vertices of a quadrilateral, but he was unable to use the PT to find common lengths of sides.  I gave him feedback that looking at sqrt(17) as a hypotenuse of a right triangle (as we had done in class) would help a bit and even wrote the PT with 17 as the hypotenuse in the hope of stimulating his memory when he did the revisions.

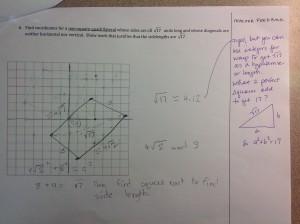
The day of the revisions Student 3 was only capable of producing this:

Student 3 revisions

He followed my direction and used 4 and 1 (which are two integers that give a hypotenuse of 17, but did not complete the problem by getting all side lengths the same. In fact, conceptually he kind of missed the boat on the fact that the sqrt(17) was supposed to be the side of the quadrilateral altogether.

 

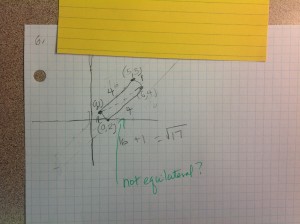
One success story was Student 2.  She also did this problem incorrectly at first by realizing that you could use 4 and 1 as the sides of a right triangle with sqrt(17) as the hypotenuse but never found the coordinates of the vertices for me. I gave her feedback saying there might be an easier way to do this because she needed vertices.  However, she was able to produce this:

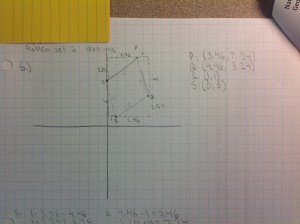
Student 2s revision
Student 2s revision

Although she did not give me integer-valued coordinates (which was not required) and she approximated which officially would not really give sqrt(17) lengths it came pretty darn close! I was impressed with the ingenuity and risk-taking that she used and the conceptual knowledge plus the skill-level. Yes, most other kids just used some combination of 1’s and 4’s all the way around but she followed her own thought pattern and did it this way.  Kudos to student 2 in my book.

Next time I will talk about some of the lessons we learned, other artifacts from the kids’ work and what we are changing for next time! Oh yeah and some great martini recipes!

Why PBL Works for Introverts

My school year is underway and as September just flew by, I have been completely overwhelmed by work – of course.  I am undertaking a new assessment method with a colleague of “feedback first and then grades” (blogpost to come when I give back the first set next week) but for now I wanted to comment on an article I just read this morning entitled “When Schools Overlook Introverts” that was posted on the Atlantic’s website.  This is a very thoughtfully written piece by Michael Godsey that is discussing how so much education is based on the idea of social constructivism which might be hard on those of us who are built to work best in “quieter, low-key environments.” This implies that the environments of collaboration and working with others are always loud, chaotic and multi-faceted.

And you know, sometimes it is.  Classrooms where kids are all at the board or working with technology can be messy.  Everyone’s talking at once, kids are calling me over and asking questions out loud (often the same questions 5 times in a row) and they are seeing themselves as the center of attention.  Once they understand, they move on and help their partner move on.  In my classroom, they take pictures with their iPads, record work in Notability or use GeoGebra to get a different perspective – either algebraic or geometric.  This can be quite chaotic.

However, most of the time in the PBL classroom.  everyone is required to sit quietly and listen to one student describe their thought process.  They need to learn to sit patiently while another student works though confusion and misunderstanding and ask questions of the presenter.  An introvert has a great deal of time of quiet to themselves being inside their head while the presenter is discussing his or her own grappling with a problem from the night before and the introvert can sit there and think, “Huh, that’s not what I did.  Should I say something and comment, or just accept that as the right answer?” The introvert grapples with different demons in the PBL classroom if they are a strong mathematics student in many ways because they might feel confident in the material but not confident that people care about their ideas.  Who knows?  It depends on their personality.

The introvert also has the opportunity to write journal entries for me and also to write bi-weekly learning reflections about what his or her learning successes were for the week.  This year I have a student with a speech impediment who was upfront with me about it at the beginning of the year.  This student has quickly become one of my best communicators because he realized how much I value what he has to say and that I would be patient and so would the rest of the class.  If he can’t say what he needs to say at the moment he wants to in class, he will always have an opportunity each week to do it.

I am very clear on my classroom contribution Assessment Rubrics that the grade does not depend on quantity of contribution, but quality.  Introverts should contribute because they have something important to add, an excellent question to make a clarifying point or something that will add depth to the conversation – never just to add to their grade. They can look at what they need to improve on by using my Student Analysis of Contribution which I will be doing next week – it’s about that time of the term.

I believe that although PBL strives to allow for all voices to be heard (both extrovert and introvert) it is the teacher that makes or breaks the classroom culture.  We need to be continually checking and rechecking the barometer of communication and tone of the class to be sure to all students are feeling heard. So that as Godsey says at the end of his article, the kids can learn with others and not by the “hell of other people.”

 

Disruption in Presence: Missing PBL Math Class

What do we all do with kids who miss out on the wonderful rich discussions where the learning happens in a PBL math class? @0mod3 asks what to do about kids’ absences. (thanks for the great question!)

It’s not as simple as “get the notes from somebody who was there” is it?  What did they actually miss by not being in class? Yes, new vocabulary possibly, new concepts, whether their problems were right or wrong – these things can all be “looked up” in some ways in another students notes or with a conversation with the teacher or a tutor just like in any other mathematics class.  So what is it we are really concerned with that they missed?

It seems that DReycer is hitting the nail on the head in her second tweet here.  Of course, it’s the experience of being a part of the rich mathematical discussions.  Hearing other students’ ideas and deciding for themselves or analyzing critically in the moment what they think of those ideas – is it right? wrong? potentially right? more efficient? similar to what I did?  These experiences are very hard to re-simulate for students who are absent from the PBL classroom.

When students come to me who have missed class.  I do tell them to look at other students’ notes.  However, this is because of how I tell students in my classes to take notes.  Kids are supposed to attempt the homework problems on one side of the notebook and then on the other side take “note of” what the other student who is presenting the problem did differently from them.  Eventually when we, as a class, come to some type of consensus about how the problem connects to a new concept or to a problem we have already done, it is then that a student should take note of the new idea as we formalize it into a theorem or new idea.

Absences will always be a problem for us who teach in the PBL classroom since we can’t recreate the in-the-moment learning that happens when a student sees another’s presentation (unless you feel like having parental consent for recording every single class, and even then you can’t really have the interaction with the student that missed it) however, what you can do is make the most of the time when each kid is there. PBL is by its nature relational learning and student and teacher presence is extremely important.  Be sure that students are the ones who are talking and asking questions in order for them to actively be engaging with the presenter.  Be sure that you are present to their needs when they return from an absence.  On days when they are not there, it might be enough for them to ask questions on the next day after they have read through the vocabulary or seen someone’s complete solution.  Sometimes active learning the next day can just be enough.

I’d love to hear other people’s ideas and thoughts!

Connections Between IBL and PBL

At the PBL Summit a few weeks ago, we had two wonderful speakers, Julian Fleron and Phil Hotchkiss from Westfield State University who are founding members of the Discovering the Art of Mathematics Project.  They gave a great key note address on Friday night about Inquiry-Based Learning and motivating students in an IBL classroom.  You can find their talk at our Summit Resources website if you are interested.  I wrote a blogpost a few years ago about my interest in IBL and the commonalities between PBL and IBL and I thought I’d reshare in honor of them.  Enjoy!

A number of years ago, I needed some kind of suport text for a Number Theory tutorial that I was doing with two rather advanced students who had gone through the curriculum at the school where I was teaching.  These two girls were advanced enough that I knew that if I used my notes and problems from my wonderful Number Theory course from college (some many years ago) we would have a great time.  I looked online and found a great book called “Number Theory Through Inquiry” published by the MAA which came with an instructor’s supplement including pedagogical discussion and some solutions.  It sounded so much like what I was doing with my other classes that I couldn’t turn down the opportunity to see what it was like.  So I ordered the book and while I was reading the instructor’s supplement I came across something that I had not heard about before (and now I am so embarrassed to admit this). The authors described what they called the “Modified Moore Method” of instruction or Inquiry-Based Learning and went on to describe what sounded interestingly so much like what I was doing in my classroom.  I had to learn about this Moore Method.

I ended up researching R.L. Moore online and it seems that he was one of the first math teachers – ever – to think about and act on this idea of not teaching mathematics with direct instruction.  He did it all the way back in 1948, but at the college level – and it was radical there!  The idea of Inquiry-Based Learning has expanded from there, but it has really only stayed at the college level in mathematics for a very long time.  There are many initiatives at the college level, including the folks at Westfield State University who are writing a wonderful curriculum project funded by the NSF called Discovering the Art of Mathematics with is a math for liberal arts curriculum at the college level.  I think it could be used at the secondary level as well for an alternative elective in the senior year for those students who still want to take a college-level math course but aren’t ready for or interested in an AP course in Calculus or Stats.  If there are any secondary teachers interested in beta-testing this unique curriculum please contact me and let me know.  I am on the advisory board for this project.

What made me think about the connection between IBL and PBL was this wonderful blogpost I just read by Dana Ernst, of Northern Arizona University in which he describes, in such wonderful ways, the pedagogy and nature of IBL.  The similarities between the definition of IBL he cites (by E. Lee May) and my definition of PBL are eerie – and it is one of the only ones that I’ve seen that stresses a reference to teacher authority being diminished.  Many wonderful resources are given by Ernst at the end of his post as well.

I do remember back in 2003, when I published my first article on my experiences at Emma Willard, after I left Exeter (where they called in Harkness teaching because of the table), in attempting to teach the way I wished to.  I had no idea what to call what I was doing.  I believe in my first article I called it teaching with a Problem-Solving Curriculum (PSC).  After I started my doctoral work, I found PBL and I realized that’s what it was.  Then I read more and more and realized that others thought PBL was project-based learning and called what I did discovery learning.  After reading about R.L. Moore, it sounds like he was doing it all along since 1948 and called it IBL.  In whatever branch of the pedagogical family tree you find yourself, if you are asking students to look at mathematics with wonder and question what they know – you should know that you are supported, know that you are doing good work and know that there is someone out there who has done it before and wants to discuss it with you.

PS – I’m hoping to attend the Legacy of R.L. Moore Conference next year in Austin, if anyone is interested!

Think about where the learning happens in PBL

2 Comments

After a few weeks of recovery, I wanted to write about having a BLAST of a time at our first attempt of putting together the PBL Summit my friend Nils Ahbel and I organized from July 16-19.  I wanted to thank all of those who came and participated in the discussions and talks and who shared their ideas so freely.  It’s such a great reminder of the huge resources we all are to each other as math teachers.  I know that I at least tripled my Professional Learning Network and hope that all of the participants did too.

I’d also like to thank everyone who gave feedback and the amazing ideas for next year – including a pre-conference session for those of you who might have been PBL “newbies” and might have needed more of an intro, topic-level groups, more in-depth SIGs for people who want to dive deeply into writing or assessment writing too.  The ideas just kept flowing and I think we will have a wonderful plan for next year too.

One of the take-aways that I left the PBL Summit with was how differently people view what “learning” means in PBL.  From my long career both teaching and studying PBL, I have had a lot of time to form my own frameworks for student knowledge construction and pedagogical theory and often take for granted that all of us are on the same page. As I have traveled and talked to many other math teachers and heard others who are experts in PBL (both PjBL and PrBL) speak, I realize more and more that we are often NOT on the same page.  This does not mean that any one of us is more right or wrong.  We just need to understand each other more.

My big question to everyone I talk to is “where/when does the learning happen?” or “where/when do the students construct their knowledge and understanding of the mathematics?”  If students are presented with a problem, for example they watch a wonderful interesting video of a basketball player shooting at a basket or watching someone fill a water tank and they come up with their own question based on a real-life phenomenon from the video, how do those students know the mathematics to answer those interesting questions?  If students are sitting through direct instruction lessons to be exposed to the mathematics but using them to answer their own questions, this is definitely an improvement than passive mathematics classes of the past.  Having students take ownership of the material in this way is is a powerful method of creating agency for mathematics learning.  The problems that they are solving and from where they are posed are extremely relevant to the motivation and agency in learning.

I would posit that PBL can be more and mean more and in more ways to student learning. Even when posed with a good problem (one they did not come up with themselves).  In PBL, students can:

  • see the need for a new method without the teacher introducing it
  • see the need for discussing other students’ ideas
  • find their own organizational strategies for problem solving
  • access prior knowledge that they did not realize they needed before
  • use their resources to discuss the problem with each other
  • use resources to find new solutions and follow their own thinking
  • make connections between topics in mathematics that they might not have realized before
  • create community in the mathematics classroom (like in other disciplines – humanities, fine arts and science)
  • realize that reflection is one of the most important parts of the learning process
  • learn to relate to others in math class
  • see mathematics as a creative endeavor

and so much more. I’d love to hear from people some that I have left out.  In my mind, even the mathematical learning happens in these contexts and students are the shapers of where and when this happens.  Robert Kaplinsky is one of those amazing PBL teacher/speakers who has a somewhat different approach than I do, but is very similar in many ways and I heard him say this April, “Don’t teach what students need to know before they do a problem-based lesson.” In that way, we are all on the same page, for sure.

Why Can’t We All Just Get Along?: Some Inquiry Math Classes are not Content-less

Maybe it’s just how I am, or maybe I’m just always worried about what people are going to say about me, but I am hesitant to criticize other teachers publicly in the blogosphere. I’ve always felt this camaraderie with others once I’ve learned they were a teacher even if we are very different from each other – different disciplines, different pedagogical styles, different countries – there are still fundamental commonalities that even public and private school teachers have.

I just finished reading a KQED blogpost entitled “Do You Have the Personality to be an Inquiry-Based Teacher?” that sort of summarizes the theoretical qualities that the author feels a teacher who would teach with IBL would need to exhibit in order to successfully run a classroom. It’s kind of interesting – I’m not sure I agree with it, but respect the author for putting his ideas out there. I’ve been an inquiry/problem-based teacher for almost 20 years and I don’t think I exhibit all of the qualities listed, so I’m not sure it’s quite true.

Anyway, that’s not the point – at the end of the blogpost there are about 11 comments from people who are educators and many of them are quite negative and even degrading to the author:

“I earned a Ph.D. in Educational Psychology, but phrases like this one still baffle me: “…the divide between a transmission model and an inquiry model…” ”

“First, we need to make sure that we have at least a rudimentary understanding of the language in which we will be teaching. Second, we need to make sure we can write.”

“That is what’s wrong with you teachers.You want to do it your way.”

“Some of us have been doing this for decades, where were you?”

Whoa, Whoa, Whoa…cowboys…hold your horses. This guy is just writing an essay about something he believes in. What kind of role model are we being for our students if this is how we are reacting to something we don’t agree with? What happened to civil communication? I totally agree that people are allowed to comment and voice their opinions on someone else’s opinion, but there has to be a way to do it with respect and decency.

So I am going to try to model what I would like to see as a response to something I actually do disagree with. Here is a blogpost by a very respectable Professor in Canada, who I have to be totally honest, I do not know at all. I tried to learn as much as possible about him before writing a response to his blogpost in order not to make any assumptions about him (and not make a fool of myself in doing so), so I may be wrong about some of this information because I garnered it from different websites. It seems he is a research mathematician who is currently studying to get a teaching degree, but who lectures for mathematics courses at the college level. I cannot ascertain if he has any experience teaching at lower levels (like elementary or secondary). From his blogpost it does seem like he takes pride in the amount of background research he does, which again is very respectable and I appreciate in bloggers. He seems to care a lot about student learning and from his opinions on his blog he seems to lean towards being a behaviorist and cognitive theorist in terms of learning theories.

His latest blogpost is titled “The Content-less Curriculum” and it is a critique of the movement towards 21st Century skills being a part of the mathematics classroom. It does sound like Prof. Penfound is implying that with the inclusion of “soft skills” of collaboration, critiquing others work, problem solving,communication, etc. (i.e. the MPS for the CCSS) there must be a loss of mathematical content. In fact, he says that

“there must be a trade-off for the inclusion of “soft skills” activities into an already packed curriculum. So what gets removed from the curriculum then? Content knowledge.”

I would respectfully, but wholeheartedly disagree with this. By teaching with the PBL curriculum that I use, I have all of the college prep geometry curriculum I desire and I also concurrently am assessing and teaching the skills of problem solving and the so-called “soft skills” that he is implying are an add-on. I still give quick quizzes to make sure that students are up on their basic skills that are so important for basic problem solving (or else they wouldn’t be able to do the open-ended problems they are given).  The mathematics that students leave my courses having experienced is rich and leaves an impression on the way they think.

Making blanket statements about teachers implying that we all make choices that are not based in research or good practice is just not true. I actually invite you Prof. Penfound to come visit my classes and see my IBL/PBL classes in practice and let me know what you think of your opinions of the rigor of the mathematics that is discussed. Although we are most likely at different ends of the spectrum in terms of learning theories, I do believe that students have different needs and try to work with kids’ learning needs individually. However, I do believe as @danieldmccabe does that there are going to be new outcomes required of our ever-growing diverse body of graduates in the near future (or even present). I also have to say that I have thought rather thoroughly about the implementation of a teaching program which includes “soft skills” and even wrote a dissertation on it.

It is possible to balance content and practice skills and it is what I and many other classroom practitioners strive for. I do not deny that there are some practitioners out there that are confused about what problem-based and project-based learning outcomes should be especially with regard to secondary mathematics, but that is a subject for another blogpost.  The balance between content and practice skills we should strive for does not mean that one is more important or less important and in fact they both need to be assessed with the ultimate goal being to create independent problem solvers. From my experience this does not necessarily happen in a classroom where the educator does not take into consideration the so-called “soft skills.” But that statement is, of course, based on my 25 years of anecdotal classroom experience.

 

Succeeding at Helping Students to Fail?? Part 1: Meaning

Apologies faithful readers – those of you who know me well, know that I have been dealing with a great deal of personal issues and preparing for the summer PBL Math Teaching Summit, so I have taken a small hiatus from blogging for a while.  However, with that under control for now, I turn to reflecting on something that happened in class the other day and its relation to a great article I retweeted that was on TeachThought’s website the other day entitled Helping Students Fail.  I have been giving a lot of thought this year to the idea of Grit and Problem-Based Learning which has intrigued me for a while.  However, this article is one of the few I’ve seen that really speaks to some concrete steps that teachers can take to aid students on the journey of dealing with making mistakes and viewing them in a positive light.

I love the framework that the author gives here:

http://www.teachthought.com/teaching/the-role-of-failure-in-learning-helping-students-fail/
Helping Students Fail: A Framework by Terry Heick

Breaking the struggle into these four aspects of learning is very interesting to me (of course with respect to the PBL Classroom).  It dawned on me while reading this article that this is a continuous and completely ongoing process of learning to fail that happens.  It is so ubiquitous that the teacher and students are probably not even aware of it (or are so aware of it that that’s where the discomfort is emanating from).  It is so ubiquitous that I needed this framework for me to be able to even have it spelled out for me.

1. Meaning: In the PBL classroom, meaning is shaped everyday – the explicit separation between knowledge and performance is spelled out in discussion and the way students are asked to share their attempts at problems.  Jo Boaler might have spelled it out best in her paper desribing the Dance of Agency, where she explained the importance of sharing what she called “partial solutions.”  Using this language is really important to make sure that students don’t feel the need to have a complete solution when they present (because no matter how many times I say it, they still say, “Is it OK if it’s wrong/”)  In their mind, they feel their presentation is a performance.  However, the other day I had an interesting experience while students were presenting.  We were doing this problem in class and I had assigned two girls to present their ideas together:

A triangle has sides measure 9, 12 and 15 (what’s special about this triangle?).  Find the distances to the centroid from all three vertices.

The day before we had done a problem very similar to this with an equilateral triangle of sidelength 6 and the presenter had realized that he could connect this problem to the work we were doing with 30-60-90 triangles.  He then applied the Centroid Theorem which states that the centroid is 2/3 of the way from the vertex along the median.  So when the girls presented, they did this:

FullSizeRender (1)

They realized that the median from A was the hypotenuse of a right triangle and they could find its length with the Pythagorean Theorem. They then used the Centroid Theorem and found 2/3 of it. However, next, they did this:


FullSizeRender (2)It was great that they connected this problem to the previous day’s presentation where all of the distances were the same (I’m always asking them to look for connections). However, when I asked them the question of whether they expected those distances to all be equal, they had to think about that. We put the question out to the class and it started a great discussion about why sometimes they were the same and sometimes they weren’t. I won’t go into the whole solution here since the correct answer is not the point of this blogpost but what happened that evening is.

Later on that night, I received an email from one of the girls who was part of the presenting team. At the end of class, I had noticed that she seemed very quiet and I had asked her if she was confused about something else we were discussing towards the end of the class when the bell rang. She had said no and left class very awkwardly.

This is what she wrote to me:

FullSizeRender
I had been working so hard to make students feel comfortable making mistakes that I wasn’t paying attention to who had made the mistakes and that they were actually comfortable making the mistakes and proud of making those mistakes and wanted credit for making those mistakes! I was dumbfounded. I just couldn’t believe it. My perception of (at least) this student’s ability to be comfortable with being wrong was so different than what her’s was. She was proud that her “mistake was a good one” and not just a “silly error” and I needed to give her the credit she deserved for taking a risk. I learned such a great lesson from this student on this day and I owe her so much (and don’t worry, I told her that in an email response)!

The separation between knowledge and performance has been made clear to at least some of my students and I am going to keep doing what I’m doing in the hope of getting this message to all of them.

Tracking, PBL and Safety in Risk-Taking

I’ve been giving a lot of thought recently to the idea of “tracking” in PBL, mostly at the prodding of the teaching fellow I’m working with this year – which is so awesome, of course.  Having a young teacher give you a fresh outlook on the practices that your school has come to know and accept (even if I don’t love them personally) is always refreshing to me.

I have taught with PBL in three different schools – two that tracked at Algebra II (or third year) point in the four-year curriculum and now one that tracks right from the start.  Anyone who has done Jo Boaler’s “How to Learn Math” course has seen the research about tracking.  So the question that my teaching fellow asked me, is why do we do it.  The answers I had for him were way too cynical for a first year student teacher to hear – “Because it’s easier for the teachers to plan lessons and assessments.” “Because the class will be easier to manage, as well as parents.”, etc.

In fact, I would have to say that in a PBL math classroom the experiences that I had with the heterogeneous groupings ended up being really advantageous for both strong and weak math students.  Here’s a great quote from a weaker student in a heterogeneously grouped math class, who was part of my dissertation research (that I have used before in presentations) when asked what the PBL math classroom was like for her:

“You could, kind of, add in your perspective and it kind of gives this sense like, “Oooh, I helped with this problem.” and then another person comes in and they helped with that problem, and by the end, no one knows who solved the problem.  It was everyone that solved the problem.  LIke, everyone contributed their ideas to this problem and you can look at this problem on the board and you can maybe see only one person’s handwriting, but behind their handwriting is everyone’s ideas.  So yeah, it’s a sense of “our problem” – it’s not just Karen’s problem, it’s not just whoever’s problem, it’s “our problem”.

This shared sense of work, I believe, rubs off on both the strong and weak students and allows for mutual respect more often than not.  Even my teaching fellow shared an anecdote from his class wherein a stronger student had gotten up to take a picture with his iPad of a solution a weaker student had just been in charge of discussing.  The presenter seemed outwardly pleased at this and said ,”He’s taking a picture of what I did? that’s weird.”

This mutual respect then leads to a shared sense of safety in the classroom for taking risks.  Today I read this tweet from MindShift:

I don’t really read that much about coding, but when something talks about risk-taking, I’m right there.  In this article, the student that decided to go to Cambodia and teach coding to teenage orphans makes a really keen observation:

“Everybody was a beginner, and that creates a much more safe environment to make mistakes.”

So interestingly, when the students in a classroom environment have the sense that they are all at the same level, it allows them to accept that everyone will have the same questions and opens up the potential that all will be willing to help.  I don’t think this has to be done with actual tracking though – I think it can happen with deliberate classroom culture moves.

I got more insight into this when asking some students in my Honors Geometry class why they don’t like asking questions in class.

“It seems to not help that much because it shows others how much I don’t know.”
“It only allows others to feel good about themselves instead of make me feel better that my question was answered.”
“If someone else can answer my question then they end up getting a big head about it instead of really helping me understand.”

I was starting to see a trend.  Now, this was not all kids, don’t get me wrong, but it was enough to get me concerned – This reminded me of a great blogpost I read by John Spencer (@edrethink) called The Courage of Creativity in which he write about how much courage it takes to put something creative out there and fail.  In mathematics, many students don’t see it as being creative, so hopefully John won’t mind if I change his quote a little bit (since I am citing him here, I hope this is alright!)

“All of this has me thinking that there’s a certain amount of courage required in [risk-taking in problem solving]. The more we care about the work [and are invested in the learning or what people think of our outcomes], the scarier it is. We walk into a mystery, never knowing how it will turn out. I mention this, because so many of the visuals I see about creativity treat creative work like it’s a prancing walk through dandelions when often it’s more like a shaky scaffold up to a mountain to face a dragon.”

Thanks John!

PBL Summit News!

It’s been an extremely busy fall for me, but with the help of my friend Nils Ahbel, I have finally put together an informational flyer and schedule for the Problem-Based Learning Math Teaching Summit for next summer.  As you begin to look for professional development opportunities for yourself, please consider being a part of this great summit where like-minded math teachers can gather and share ideas.  Currently, we are making this information available and registration and final pricing will be available in January.  If you have any questions regarding the summit, please feel free to contact me.

Check out the PBL Math Summit Flyer 2015 here. For further information see the page on the PBL Summit.

How do we get kids to value others’ ideas in math class?

Some recent common situations:

A very gifted student comes to me (more than once) after class asking why he needs to listen to other students talk about their ideas in class when he already has his own ideas about how to do the problems.  Why do we spend so much time going over problems in class when he finished all the problems and he has to sit there and listen to others ask questions?

A parent asks if their child can study Algebra II over winter break for two weeks and take a placement test in order to “pass out” of the rest of the course and not have to take mathematics.  A college counselor supports this so that they can move forward in their learning and get to Calculus by their senior year.

Tweet from a fellow PBL teacher:


Over the summer, a student wants to move ahead in a math course and they watch video after video on Khan Academy and take a placement test that allows them to move ahead past geometry into an Algebra II course.  Why would they need to spend a year in a geometry course when they have all of the material they need in 5 weeks of watching videos all alone?

It is a very accepted cultural norm in the U.S. that math is an isolated educational experience.  I’m not quite sure where that comes from, but for me, it remains a rather traditionalist and damaging view of mathematical learning.  I would even go so far as to say that it could be blamed for the dichotomous view of mathematics as black or white, right or wrong, fast or slow, etc.  For many students, if they don’t fit that mold of a mathematics learner who can learn math by watching someone do it, sitting nicely and taking notes for 45 minutes while we ‘cover’ section 2.4 today, then they are ‘bad at math.’

Leone Burton once said that the process of learning mathematics is an inherently social enterprise and that coming to know mathematics depends on the active participation in the enterprises so valued and accepted in that community (Burton, 2002).  In other words, if we accept the status quo of the passivity of mathematics learning that is what we will come to believe is valued.   In her research on the work of research mathematicians and their mathematical learning she found that the opposite of the status quo was true.  The collaborative nature of their practice had many benefits that mathematicians could claim including sharing work, learning from one another, appreciating the connections to others’ disciplines and feeling less isolated (Grootenboer & Zevenbergen, 2007).  Collaboration was highly valued.

We are doing students a disservice if we allow them to remain in the status quo of being passive mathematics students or thinking that they do not have to share and/or listen to others.  The CCSS are asking (well, requiring) them to critique others’ work and give feedback on problem solving methods.  They need to be able to say what they think about others’ ideas and construct their own argument.  How are they going to learn how to express their reasoning if they don’t listen to others and attempt to make sense of it?

When working and/or learning in isolation students are not asked to do any of this or even asked to make mathematical sense oftentimes.  They are just asked to regurgitate and show that they can repeat what they have seen.  How do we know they are making any sense if they do not have to respond to anyone or interact with a group?  The importance of the social interaction becomes apparent in this context.

So what I try to explain to students is that mathematics means more to me than just being able to have a concept “transmitted” to them by someone showing them how to do something, but for them to actually do mathematics in a community of practice.  Creating that community takes a lot of work and mutual respect, but it’s something that is definitely worth it and I encourage everyone to keep inspiring me to keep doing it!  Thanks @JASauer.