Category: Problem based learning

I’ve looked at life from both sides now…

4 Comments

This past July, I spent a few days at the MAA Mathfest in Chicago for the first time. The main reason I went was because the Academy of Inquiry-Based Learning was having a Conference within the Mathfest with the theme of “Diversity in IBL.”  IBL is generally what college faculty call the type of teaching and learning that many of us at the secondary level has been calling PBL for years.  I was so interested to hear many mathematics professors talking about the struggles of writing curriculum, dealing with facilitating discussion, using writing – all of the same parts of this type of teaching that we may have been talking about for so any years.  I highly suggest that we could benefit from talking to each other.  If you would like to get involved with this movement, Stan Yoshinobu, the Director of the Academy of Inquiry-Based Learning, has put forth some challenges for his community.  Check them out.

One of the most interesting talks that I attended was by a professor from Denison University, Lew Ludwig, titled, “Applying Cognitive Psychology to the Mathematics Classroom.”  As a devout social constructivist, I generally like going to talks where I can learn more about other views of education.  Seeing both sides definitely helps me understand many of the views of my colleagues and see if evidence supports my own perspective. Ludwig had published a review of another article that was titled, “Inexpensive techniques to improve education:  Applying cognitive psychology to enhance educational practice”(Roediger and Pye, 2012).

Basically, the presentation summarized three simple techniques that cognitive psychology had evidence helped student learning. The three techniques were called

  1. The distribution and interleaving of material and practice during learning.
  2. Frequent assessment of learning (test-enhanced learning, continual assessment)
  3. Explanatory questioning (elaborative interrogation and self explanation; having students ask themselves questions and provide answers or to explain to themselves why certain points are true).

In the original article, the authors write:

“Repetition of information improves learning and memory. No
surprise there. However, how information is repeated determines
the amount of improvement. If information is repeated back to back
(massed or blocked presentation), it is often learned quickly but
not very securely (i.e., the knowledge fades fast). If information is
repeated in a distributed fashion or spaced over time, it is learned
more slowly but is retained for much longer”

When this was reported, I was first in shock.  I couldn’t believe I was hearing something in a presentation about Cognitive Psychology that was actually supported by the definition of PBL that I use.  The curriculum I use takes the idea of looking at topics and teaching them over a longer time span, but distributed among other topics.  I have called this decompartmentalization of topics, which helps students see the connectedness of mathematics.

The second idea, consistent assessment, is based on the concept that testing is not really a great measure of how much a student has learned, but it actually solidifies the learning that has occurred.  So three groups of students were given different ways of learning by reading a passage of information. The first group read a passage four times. The second group read the passage three times and had test.  The third group read the passage once and was tested three times.  Their performances on tests on the information in the passage 5 minutes later and then one week later.

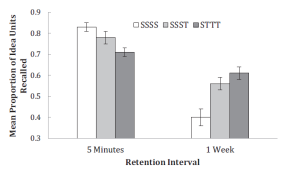
Diagram of retention testing research
from Roediger & Pye (2012) p.245

So if we connect the idea that testing is not the best method of seeing how much students have learned and the fact that consistent assessment actually helps students retain their knowledge, what I do in my PBL classrooms, is not only “test” but do all sort of forms of assessment (writing, oral assessment, hand-in homework with feedback, labs, quizzes, problem sets, self-assessment, etc.) alternately throughout the term.  There is probably not a week where students are not assessed in at least 2 ways. I feel that this has led students to have good retention of material and the assessments are strong measurements of their learning.

The last one was the one I was most excited to hear about – explanatory questioning.  This seemed to give students so much more responsibility for their own learning than traditional cognitive psychology as I had understood it.  The authors of this study claim that explanatory questioning can be broken in to two areas:

Elaborative Interrogation – students generating plausible explanations to statements while they are studying and learning.  This speaks directly to the idea of mathematical discussion and how students generate explanations when they ask themselves “why?”

Self-Explanation – students monitoring their learning and describing, either aloud or silently some features of their learning.  This idea can be found all over the PBL classroom but in mine, it’s generally found most in metacognitive journaling where students use self-explanation the most.

“Obviously, the elaborative interrogation and self explanation are related because both strategies encourage or even require students to be active learners, explaining the information to themselves (perhaps rephrasing in language they understand better) or asking themselves why the information is true.”

I honestly couldn’t believe what I was reading – this is an article on educational methods based on cognitive psychology that is suggesting that we require students to be active learners and “explain the infomation to themselves”?  This is lunacy.  I have been teaching for 25 years where students have been complaining to their parents that they have had to explain things to themselves – who would’ve known that I was applying cognitive psychology?

My guess is that these ideas are only enhanced by the social aspect of the classroom and other constructivist ideas – clearly the constructivitst classroom in enhanced by or agrees with some of these cognitive psychology methods as well.  Listening to both sides of the theories is actually helpful and I’m seriously going to continue doing this! Although I never thought that there might be strong connections between cognitive psychology theories and PBL, I do know that it’s life’s illusions I recall and I “really don’t know life, at all.”

PBL and second language learners

2 Comments

As I am not going to be in the classroom next year, I have been going through some old boxes from my study and as many people who have been teaching for a long time have, I have boxes and bags full of cards from past students.  I spent the afternoon one day going through these, reminiscing about so many great kids that I remember.  One of them I had a card from the beginning of her freshman year and also one from the end of her senior year.  Crazy!!

I don’t claim to be an expert in emergent English language learners and mathematics at all.  I did have 10 years of teaching experience at a school (Emma Willard) where they had an ESL program and many students came into my mathematics classes who were not proficient in the English language.  I do think those girls knew what they were getting themselves into and were up to the challenge, but some of them were very frightened.

Since she has now been out of college for a while, I would assume it’s ok for me to share this on my blog.  Here is the card she gave me as a new student in 2001:

Jinsup's card from freshman year
Jinsup’s card from freshman year

This card was written with the voice of a student who was used to a very structured, repetitive mathematics class and I believe she knew that coming into the U.S. things would be different, but possibly not as different as they were in my class.  When she said, “I’m so nervous that you will let me to talk a lot in the class” I’m sure she was saying that she was nervous that I would expect her to contribute to the class discussion.  What I did with many of those students, including Jinsup, was I focused in the beginning on letting them listen and write.  I gave them lots of feedback on their journals and made sure they had the correct vocabulary and that their grammar in their writing made sense.  I allowed them to ask more questions initially than to present their ideas until their confidence became stronger.  Jinsup, as most Korean and Japanese students did, had excellent skills, as that was what their math education had focused on since elementary school.  However, she was not very good at reasoning, sense-making or critical thinking on her own.  It was almost as if she had not been asked to communicate about mathematics, as she was trying to say in her note to me.

However, she ended up doing very well in that first class and then I taught her again in precalculus (which we called Advanced Math) and then in BC Calculus her senior year.  Her excellent background allowed her to focus on the reasoning aspects of all of these courses and in the end, I was very impressed with her growth.  She really got the best of both worlds – the skills from her Asian mathematics education and the collaboration, communication and reasoning skills from the PBL here.

This is the note she wrote me at the end of her senior year:

Jinsup's card at end of her senior year
Jinsup’s card at end of her senior year

Although I know this is only an anecdote and I don’t really have research evidence that PBL totally works with ELLs I do have confidence that with the right environment and patience, it is actually a great way of teaching for many of these second language learners.  It allows them to find their voice in a language that is already new to them but at the same time have some practice in terminology that they may have heard before.  I think this might be my next interesting research project – if anyone has some thoughts on this I’d love to hear them.

Yours, Mine and Ours

Yesterday we had a speaker in our faculty meeting who came to talk to us about decision-making process in our school.  He spoke about the way some colleges, universities, independent schools are very different from businesses, the military, and other governing bodies that have to make decisions because we are made up of “loosely-coupled systems.” These are relationships that are not well-defined and don’t necessarily have a “chain of command” or know where the top or bottom may be.  They also don’t necessarily have a “go-to” person where, when a problem arises, the solution resides in that location.  The speaker said that this actually allows for more creativity and generally more interesting solution methods.

About mid-way through his presentation he said something that just resonated with me fully as he was talking about the way these systems come to a decision cooperatively.

“The difference between mine and ours is the difference between the absence and presence of process.”

Wow, I thought, he’s talking about PBL.  Right here in faculty meeting.  I wonder if anyone else can see this.  He’s talking about the difference between ownership of knowledge in PBL and the passive acceptance of the material in a direct instruction classroom.

Part of my own research had to do with how girls felt empowered by the ownership that occurred through the process of sharing ideas, becoming a community of learners and allowing themselves to see others’ vulnerability in the risk-taking that occurred in the problem solving.  The presence of the process in the learning for these students was a huge part of their enjoyment, empowerment and increase in their own agency in learning.

I think it was Tim Rowland who wrote about pronoun use in mathematics class (I think Pimm originally called it the Mathematics Register). The idea of using the inclusive “our” instead of “your” might seem like a good idea, but instead students sometimes think that “our” implies the people who wrote the textbook, or the “our” who are the people who are allowed to use mathematics – not “your” the actual kids in the room.  If the kids use “our” then they are including themselves.  If the teacher is talking, the teacher should talk about the mathematics like the are including the students with “your” or including the students and the teacher with “our”, but making sure to use “our” by making a hand gesture around the classroom.  These might seem like silly actions, but could really make a difference in the process.

Anyway,  I really liked that quote and made me feel like somehow making the process present was validated in a huge way!

Repost: Always Striving for the Perfect Pose

2 Comments

Back in 2010, I wrote an blogpost comparing teaching with PBL to doing yoga. Since I have been doing Bikram Yoga for almost a year now and still can’t do “standing head to knee pose” *at all* – I thought I would repost this one just to give myself some perspective, and possibly many of you out there who might need a little encouragement at this beginning of the year time. I know that every year when students begin a year in a PBL math class the obstacles return. Parents are questioning “why isn’t the teacher teaching?” Students are questioning “why is my homework taking so long?” Teachers new to the practice are questioning “When is this going to get easier?” and “why aren’t they seeing why this is good for them like I do?” The best thing to remember is that it is a process and to understand how truly different and hard it is for students who are used to a very traditional way of learning mathematics. Give them time, have patience for them and yourself and most of all reiterate all of what you value in their work – making mistakes, taking risks, their ideas (good and bad) and be true to the pedagogy.

Here’s the original blogpost I wrote:

I don’t think my professor, Carol Rodgers, would mind me borrowing her yoga metaphor and adapting it to PBL. I use it often when talking to teachers who are nervous about falling short of their ideal classroom situation or teaching behaviors. I think this can happen often, especially when learning best practices for a new technique like facilitating PBL. There are so many things to remember to try to practice at your best. Be cognizant of how much time you are talking, try to scaffold instead of tell, encourage student to student interaction, turn the questions back onto the students, etc. It really can be a bit overwhelming to expect yourself to live up to the ideal PBL facilitator.

However, it is at these times that I turn to Carol’s yoga metaphor. She says that in the practice of yoga there are all of these ideal poses that you are supposed to be able to attain. You strive to get your arms, legs and back in just the right position, just the right breathing rhythm, just the right posture. But in reality, that’s what you’re really doing – just trying. The ideal is this goal that you’re aiming for. Just like our ideal classroom. I go in everyday with the picture in my head of what I would want to happen – have the students construct the knowledge as a social community without hierarchy in the authority where everyone’s voice is heard. Does that happen for me every day? Heck no. I move the conversation in that direction, I do everything in my power for that to happen, but sometimes those poses just don’t come. Maybe I just wasn’t flexible enough that day, or maybe the students weren’t flexible enough, maybe we didn’t warm up enough, or the breathing wasn’t right. It just wasn’t meant to be. I have exercises to help me attain the goal and I get closer with experience. That’s all I can hope for.

So I tell my colleagues who are just starting out – give yourself a break, be happy for the days you do a nearly perfect downward facing dog, but be kind to yourself on the days when you just fall on your butt from tree pose. We are all just trying to reach that ideal, and we keep it in mind all the time.

Getting Kids to Drive the Learning

2 Comments

It doesn’t always work this way, but it would be awesome if it did.  When PBL is perfect or ideal, the students are the ones who make the natural connections or at least see the need or motivation for the problems that we are doing.  Yeah, some of them are just really interesting problems and the get pulled in by their own curiosity, but as all math teachers know, we have a responsibility to make sure that students learn a certain amount of topics, it is quite that simple.  If students from my geometry class are going into an algebra II class with trigonometry the next year where their teacher will expect them to know certain topics, I better do my job and make sure they have learned it.

So how do I, as a PBL teacher, foster the values for the problem-based learning that I have while at the same being true to the curriculum that I know I have a responsibility to?  This is probably one of the biggest dilemmas I face on a daily basis.  Where’s the balance between the time that I can spend allowing the students to struggle, explore, enjoy, move through difficulty, etc. – all that stuff that I know is good for them – while at the same being sure that that darn “coverage” is also happening?

So here’s a little story – I have a colleague sitting in on my classes just to see how I teach – because he is interested in creating an atmosphere like I have in my classes in his.  We have just introduced and worked on problems relating to the tangent function in right triangle trigonometry in the past week and now it was time to introduce inverse tangent.  I do this with a problem from our curriculum that hopefully allows students to realize that the tangent function only is useful when you know the angle.FullSizeRender (3)

So as students realize they can’t get the angle from their calculator nor can they get it exactly from the measurement on their protractor (students had values ranging from 35 to 38 degrees when we compared), one of the students in my class says, “Ms. Schettino, wouldn’t it be great if there was a way to undo the tangent?” and the other kids are kind of interested in what she said. She continues, “Yeah, like if the calculator could just give us the angle if we put in the slope.  That’s what we want.”  I stood there in amazement because that was exactly what I wanted someone to crave or see the need for.  It was one of those “holy crap, this is working” moments where you can see that the kids are taking over the learning.  I turned to the kids and just said, “yeah, that would be awesome, wouldn’t it?  Why don’t you keep working on the next problem?” and that had them try to figure out what the inverse tangent button did on their calculator.  They ended up pressing this magical button and taking inverse tangent of 0.75 (without telling them why they were using 0.75 from the previous problem) to see if they could recognize the connection between what they had just done and what they were doing.

At the end of the class, the colleague who was observing came up to me and said, “How did you do that?” and I said, “What do you mean?” and he said, “How did you get the kids to want to learn about inverse tangent? I mean they just fell right into the thing you wanted them to learn about.  That was crazy.”  I really had to think about that.  I didn’t feel like I did anything honestly, the kids did it all.  I mean what made them all of a sudden care about getting the angle?  Why were they invested?   It doesn’t always happen in my classroom that’s for sure.  This is not a perfect science – there’s no recipe for it to work – take a great curriculum, interested kids, an open, respectful learning environment and mix well?

I do think however that a huge part of it is the culture that has been created throughout the year and the investment that they have made in their ownership and authorship in their own learning. We have valued their ideas so much that they have come to realize that it is their ideas and not mine that can end up driving the learning – and yes, I do end up feeling a little guilty because I do have a plan.  I do have something that I want them to learn, but somehow have created enough interest, excitement and curiosity that they feel like they did it.  It is pretty crazy.

Considering Inclusion in PBL

It’s always refreshing when someone can put into words so eloquently what you have been thinking inside your head and believing for so long.  That’s what Darryl Yong did in his recent blogpost entitled Explanatory Power of the Hierarchy of Student Needs.  I feel like while I was reading that blogpost I was reading everything that I had been thinking for so long but had been unable to articulate (probably because of being a full time secondary teacher, living in a dorm with 16 teenage boys, being a mother of two teenagers of my own and all the other things I’m doing, I guess I just didn’t have the time, but no excuses).  Darryl had already been my “inclusive math idol” from a previous post he wrote about radical inclusivity in the math classroom, but this one really spoke to a specific framework for inclusion in the classroom and how in math it is necessary.

 

In my dissertation research, I took this idea from the perspective of adolescent girls (which, as I think towards further research could perhaps be generalized to many marginalized groups in mathematics education) and how they may feel excluded in the math classroom.  These girls were in a PBL classroom that was being taught with a relational pedagogy which focuses on the many types of relationships in the classroom (relationship between ideas, people, concepts, etc.)  – I did not look at it from the perspective of Maslow’s Hierarchy of Student Needs and this is really a great tool.

Interestingly,  I came up with many of the same results. My RPBL framework includes the following (full article in press):

  1. Connected Curriculum– a curriculum with scaffolded problems that are decompartmentalized such that students can appreciate the connected nature of mathematics
  2. Ownership of Knowledge – encouragement of individual and group ownership by use of journals, student presentation, teacher wait time, revoicing and other discourse moves
  3. Justification not Prescription– focus on the “why” in solutions, foster inquiry with interesting questions, value curiosity, assess creativity
  4. Shared Authority – dissolution of authoritarian hierarchy with deliberate discourse moves to improve equity, send message of valuing risk-taking and all students’ ideas

These four main tenets were what came out of the girls’ stories.  Sure many classrooms have one or two of these ideas.  Many teachers try to do these in student-centered or inquiry-based classrooms.  But it was the combination of all four that made them feel safe enough and valued enough to actually enjoy learning mathematics and that their voice was heard. These four are just a mere outline and there is so much more to go into detail about like the types of assessment (like Darryl was talking about in his post and have lots of blogposts about) the ways in which you have students work and speak to each other – how do you get them to share that authority when they want to work on a problem together or when one kid thinks they are always right?

The most important thing to remember in PBL is that if we do not consider inclusion in PBL then honestly, there is little benefit in it over a traditional classroom, in my view. The roles of inequity in our society can easily be perpetuated in the PBL classroom and without deliberate thought given to discussion and encouragement given to student voice and agency, students without the practice will not know what to do.  If we do consider inclusion in the PBL classroom, it opens up a wondrous world of mathematical learning with the freedom of creativity that many students have not experienced before and could truly change the way they view themselves and math in general.

Revisiting Journals: Getting Kids to Look Back

I have been using metacognitive journaling in my PBL classroom since 1995.  I first learned about it the Summer Klingenstein Institute when I was a third year teacher and just fell in love with it.  At that time, the colleagues at my school thought I was crazy trying to make kids write in my classes – it was just “something else for them to do” and didn’t really help them learn but I did more reading on it and there was clearly more and  more research as time went on that showed that writing-to-learn programs especially those that prompt for metacognitive skills really do help in learning mathematics (see my metacognitive journaling link under the Research tab for more info and sample journal entries).

Every once in a while a student will write a journal entry that I think is so thoughtful that I will write about it like this one a few years ago that just impressed me with his insight into his learning process of a particular problem. But other times kids write about their understanding of their learning overall like one I’ll write about today and I am also blown away.

Here’s a student I’ll call Meaghan reflecting on a problem that she found challenging for her.  Really, it doesn’t matter which problem it was or what topic it was, just the fact that she had a hard time with it at first, right?  The most important part was that after she wrote about how to do it correctly, she then took the time to write this: (in case you can’t read her handwriting, I will rewrite it below).

FullSizeRender
Part of Meaghan’s Journal Entry

“This problem was a challenge for me.  When I saw the question, it didn’t look that difficult but once I was trying to solve by [sic my] brain wasn’t thinking on the right track, and it was trying to use prior knowledge that was irrelevant in this case.  I wasn’t making connections to the properties of triangles that I had recently learned.”

Why is this realization so important for Meaghan?  Polya’s Fourth Principle of Problem Solving is “Look Back” – why is this fourth principle so important?  In my mind, this is where all the learning happens.  The three other principles are very clear

  1. Understand the problem
  2. Device a plan
  3. Carry out the plan

These three are all very basic – if they work, right?  But most of the time they don’t work for kids.  It’s the fourth step that we know is the most important – it’s where the critical thinking and analysis takes place.  If this part isn’t taken seriously and the right steps within it are not taken nothing happens, no moving forward, no growth.

So what did Meaghan do?  She realized that she had not made a connection between the triangle properties that we had just learned and how it applied to this problem.  She had not use the correct prior knowledge.  She  just created more openings to other knowledge that she knows- and I know what you’re thinking.  Does this mean that next time she will use the correct prior knowledge in another problem?  From my experience with kids, no, it does not.  But honestly, what I have seen is that the more they realize that there are more possibilities and also that the option of just saying “I don’t get it” or “I can’t do this” is unlikely, the more they will keep trying.

So what did Meaghan do? By just being asked to write a reflection about one problem (every two weeks) she has reinforced her own potential in problem solving on HER OWN.  That she may, in the future, weed out the irrelevant prior knowledge and possibly see the connections to the relevant prior knowledge, with more practice.  I think it’s made her feel just a little bit more confident – and they said it was just “something else for them to do.”

Everything Old is New Again…(or why teaching with PBL is so great)

So I heard that what everyone is saying about the new Star Wars Movie, The Force Awakens, is that “Everything Old is New Again” – go ahead google it, there are at least 5 or 6 blog posts or articles about how “BB-8 is the new R2D2” or “Jakku is the new Tattoine” or whatever.  I actually don’t have a problem with J.J. Abrams reusing old themes, character tropes or storylines because I think that really great stories are timeless and have meaning and lessons that surpass the movie that you are watching.  I still thought it was awesome.

This concept of everything old is new again really hit home to me today in my first period class when I was having the students do a classic problem that I probably first did in 1996 while I was under the tutelage of my own Yoda, Rick Parris (who I think wrote the problem, but if someone reading this knows differently, please let me know).  The problem goes like this:

Pat and Chris were out in their rowboat one day and Chris spied a water lily.  Knowing that Pat liked a mathematical challenge, Chris announced that, with the help of the plant, it was possible to calculate the depth of the water under the boat.  When pulled taut, directly over its root, the top of the plant was originally 10 inches above the water surface.  While Pat held the top of the plat, which remained rooted to the lake bottom, Chris gently rowed the boat five feet.  This forced Pat’s hand to the water surface.  Use this information to calculate the depth of the water.

What I usually do is have students get into groups and put them at the board and just let them go at it.  Today was no exception – the first day back from winter break and they were tired and not really into it.  At first they didn’t really know what to draw, how to go about making a diagram but slowly and surely they came up with some good pictures. Some of the common initial errors is not adjusting the units or mislabeling the lengths.  However, one of the toughest things for students to see eventually is that the length of the root is the depth of the water (let’s call it x) plus the ten inches outside of the water’s surface.  Most students end up solving this problem with the Pythagorean Theorem – I’ve been seeing it for almost 20 years done this way.  Although I never tire of the excitement they get in their eyes when they realize that the hypotenuse is x+10 and the leg is x.

However, since everything old is new again, today I had a student who actually is usually a rather quiet kid in class, not confused, just quiet, but in a group of three students he had put his diagram on a coordinate plane instead of just drawing a diagram like everyone else did.  This intrigued me.  He initially wrote an equation on the board like so:

y= 1/6 (x – 0)+10

and I came over and asked him about it.  He was telling me that he was trying to write the equation of one of the sides of the triangle and then I asked him how that was going to help to find the depth of the water.  He thought about that for a while and looked at his partners. They didn’t seem to have any ideas for him or were actually following why he was writing equations at all.  He immediately said something like, “Wait, I have another idea.” and proceeded to talk to his group about this:

Jacksons solution to Pat and Chris
Jackson’s Solution to the Pat & Chris Problem

He had realized from his diagram that the two sides of the triangle would be equal and that if we wrote the equation of the perpendicular bisector of the base of the isosceles triangle and found its y-intercept he would find the depth of the water.  He proceeded to find the midpoint of the base, then the slope of the base, took the opposite reciprocal and then evaluated the line at x=0 to find the y-intercept.  I was pretty impressed – I had never seen a student take this perspective on this problem before.

This made my whole day – I was really dreading going back to work after vacation and honestly, first period was the best class of the day when this wonderful, new method was shown to me and this great experience of this student’s persistence refreshed my hope and interest in this problem.  Perpendicular bisectors are the new Pythagorean Theorem!

Someday I’ll get this assessment thing right… (Part 2 of giving feedback before grades)

3 Comments

So, all assessments are back to the students, tears have been dried and we are now onto our next problem set (what we are calling these assessments).  What we’ve learned is that the rubric allowed us to easily see when a student had good conceptual understanding but perhaps lower skill levels (what we are used to calling “careless mistakes” or worse). We could also quickly see which problems many students had issue with once we compared the rubrics because, for example, problem number 6 was showing up quite often in the 1 row of the conceptual column.  This information was really valuable to us.  However, one thing we didn’t do was take pictures of all of this information to see if we could have a record of the student growth over the whole year. Perhaps an electronic method of grading – a shared google sheet for each student or something to that effect  might be helpful in the future – but not this day (as Aragorn says) – way too much going on right now.

We also changed the rubric a bit for a few reasons.  First, we found that when students completed the problem to our expectations on the initial attempt we felt that they should just receive 3’s for the other two categories automatically.  We considered not scoring them in this category but numerically felt that it was actually putting students who correctly completed a problem at a disadvantage (giving them fewer overall points in the end). Second, we also changed the idea that if you did not write anything on the revisions you earned 0 points for the revisions columns.  Many students told me afterwards that they felt like they just ran out of time on the revisions and actually had read the feedback.  This was unfortunate to me since we had spent so long writing up the feedback in the hope that the learning experience would continue while doing revisions.

Here is the new version of the rubric: Revised Problem Set Grading Rubric new

What we decided to do was to try the revisions this time without the “explanation” part of writing.  I think it will keep the students focused on reading the comments and attempting a new solution.  I was frankly surprised at how many students stuck to the honor pledge and really did not talk to each other (as they still got the problem wrong the second time around – with feedback).  Truly impressive self-control from the students in my classes and how they were sincerely trying to use the experience as a learning opportunity.

I do think the second assessment will go more smoothly as I am better at doing the feedback and the rubric grading.  The students are now familiar with what we are looking for and how we will count the revisions and their work during that time.  Overall, I am excited about the response we’ve received from the kids and hope that this second time is a little less time-consuming.  If not, maybe I’ll just pull my hair out but I’ll probably keep doing this!