As I write curriculum, I am constantly scouring the Internet for ideas and ways to improve my own work, as we all do. I was just on the NCTM resources page the other day at their “Reasoning and Sense Making Task Library” and found this description of a task called “As the Crow Flies”:
“The distance formula is often presented as a “rule” for students to memorize. This task is designed to help students develop an understanding of the meaning of the formula.”
OK, wait – shouldn’t this just say, we shouldn’t be presenting the distance formula as a rule for students to memorize? Instead we should be teaching it for understanding from the conceptual level and allowing students to realize the connection between the Pythagorean idea of distance and how it allows a student to find the distance between two points? Why should we have a specific task designed to create the understanding after learning the formula when the formula is actually secondary?
There is a series of questions in the problems I have written/edited that allow students to come to this realization on their own.
First, a few basic Pythagorean Theorem problems to practice the format, remind themselves of simplifying radicals, Pythagorean Triples, etc. Second, some coordinate plane review such as:
- Given A=(5,-3) and B=(0.6). Find the coordinates of a point C that makes angle ACB a right angle.
This is really an interesting discussion question for many reasons. First many students have trouble understanding where the right angle is supposed to be. If they incorrectly read that the angle that should be right is ABC, then they are picturing a different right angle (and also doing a harder problem that we’ll get to soon!) but if they are reading ACB, it’s still an interesting question because there is more than one answer.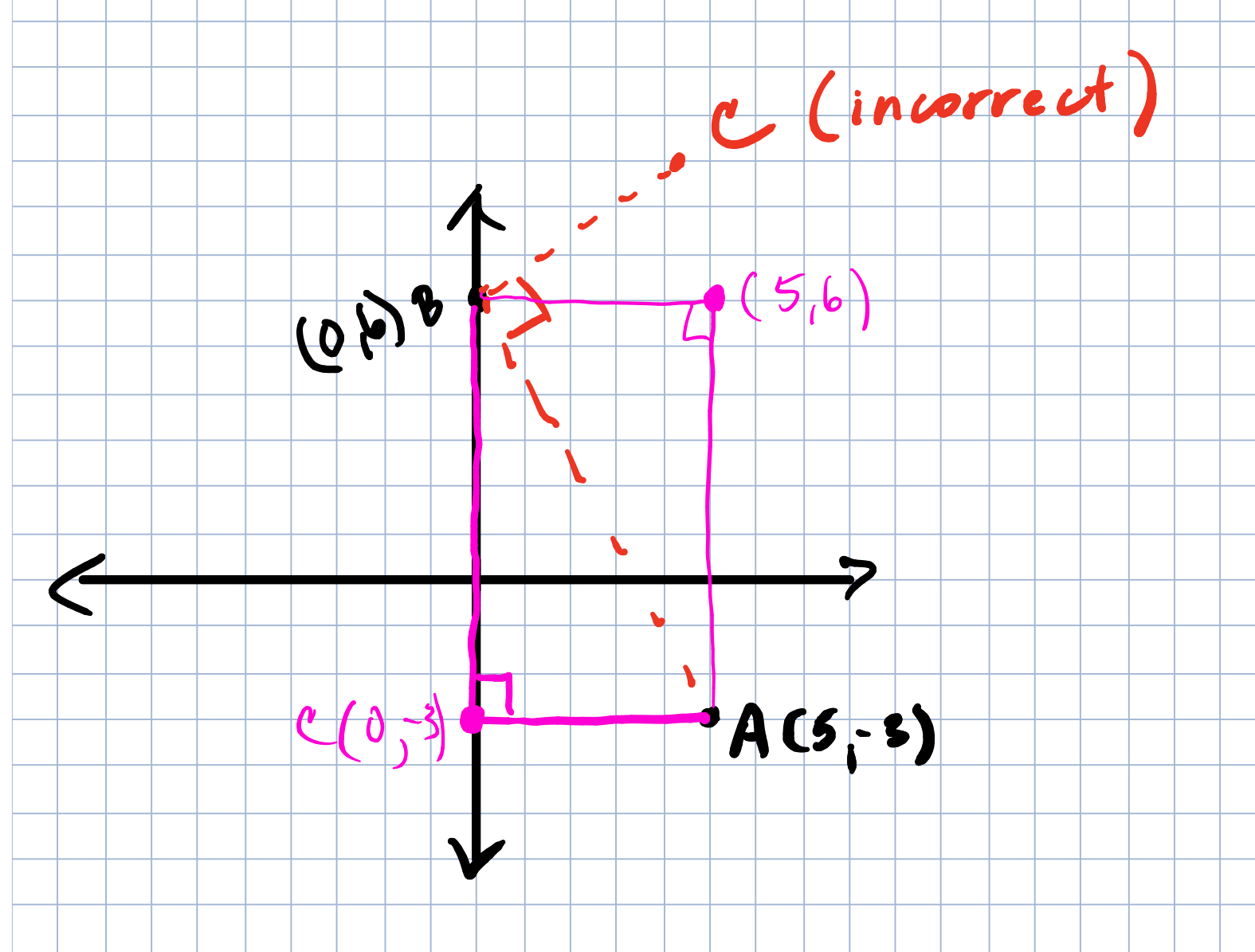
Students can sometimes visualize where the right angle can be (even both of the points) but may not be able to get the coordinates. This discussion is important however because in order to come up with the distance formula later in general (with the x’s, y’s and subscripts – whoa, way confusing!) they need to realize what’s so special about that vertex’s coordinates. So if there is a student who is confused I usually ask the student presenting this problem, “Can you describe the way you found the coordinates for C?” Their answer usually goes something like this: “You just take the x of the one it’s below and y of the one it’s next to.” and other kids are either totally on board, or totally confused. So then they need to make it a little more mathemtical so every else is on board. Other kids often chime in with words like horizontal and vertical, x-coordinate and y-coordinate. This is a really fun, useful and fruitful mathematical discussion in my experience.
We can then move to a problem like this:
2. Find the length of the hypotenuse of a right triangle ABC, where A = (1,2) and B = (5, 7). Give your answer is simplest radical form.
This is generally a problem that is given to students individually to grapple with for homework or in class in groups at the board. After doing the one discussed above, they at least are prepared to find the vertex of the right triangle and see where it should be.
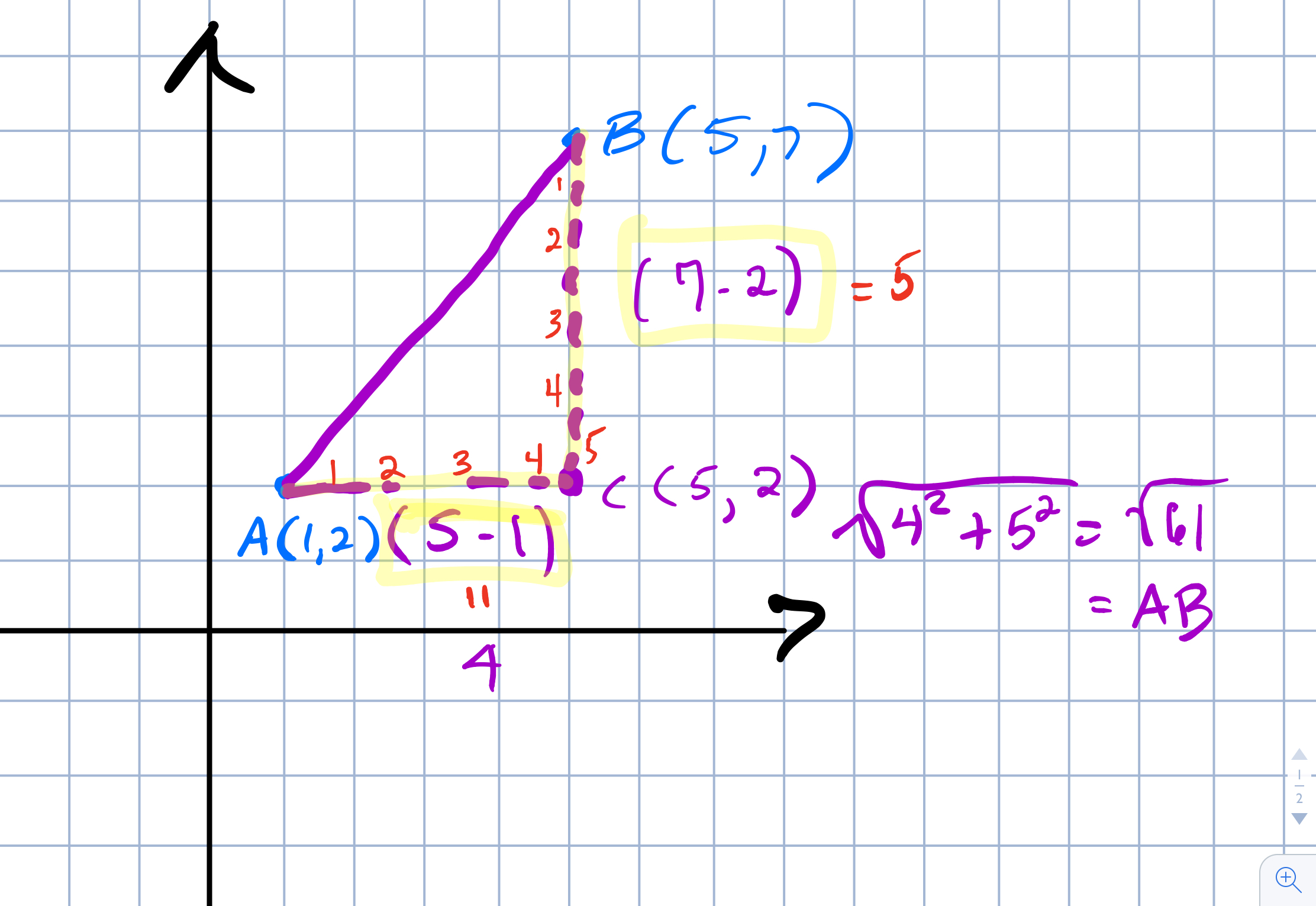
It’s honestly rare that a student can’t even draw the diagram – especially if they can make the connection with the previous problem. (Connection is one of the four pillars of the PBL Classroom). One of the things that is often difficult for students is the idea of subtraction of the coordinates. The can easily count the units to get the sizes of the legs in order to do the Pythagorean Theorem, but in order to generalize, for a later purpose…sorry, don’t want to steal the thunder…subtraction would be an interesting alternate solution method if someone comes up with it – and they usually do.
At this point if someone does come up with it, I usually do ask why can you subtract the coordinates like that to get the lengths of the sides and (you guessed it) there was an earlier problem that had student finding distance on a number line, so, many kids make that connection.
So finally we get to this, maybe a couple of problems later:
Again, students are asked to use their prior knowledge and contemplate a way that they might be able to describe of finding a way to express the distance between two points in a plane. This is after discussing notation, discussing how to visualize that distance, discussing subscripts, and discussing the purposes (in other problems) of why we might actually need to find the distances between two points. Because the Pythagorean Theorem squares the lengths of the sides (BC and AC) I’ve never had a kid get all upset about the fact that we don’t put the absolute value signs around the difference for the sides – we’re gonna square it anyway, so who cares if it’s negative? Kids usually say, “if it’s negative, let’s just subtract the other way and it’s be positive.” We just get right to the point that all we are finding is the hypotenuse of a right triangle which has been the Pythagorean Theorem all along.
I generally have students write a journal entry about this amazing revelation for them at the beginning of the year and voila! It’s right there for them, in their journal for the whole year – no memorization needed. They understand the concept, know how to use it and actually love the idea because now they can just see a right triangle every time they need a distance. It’s how so many of my students say that have “never learned the distance formla” – they just use the Pythagorean theorem to find distance. I love it.
