Category: In the classroom

Minimizing Shame in the PBL Classroom…and maybe Daring Greatly?

I recently read a blogpost by one of my favorite authors, Brene Brown, of TED talk fame, and the author of a great book about vulnerability called Daring Greatly.  In her blogpost Brene wrote about some reactions to a comment she made on Oprah Winfrey’s Super Soul Sunday show where she talked about shame in schools about which she received a great deal of criticism in the blogosphere and on twitter.

I kept reading as I was shocked that anyone would be offended by anything that Brene Brown could say – especially teachers.  She has always been extremely inspiring and very supportive of teachers – as a teacher herself, her book, Daring Greatly, has a whole chapter on how schools can support a community to come together around vulnerability and become closer and foster creativity and innovation in this way.

However, she talks about the research that she has done about learning and teaching.  She says,

“As a researcher, I do believe that shame is present in every school and in every classroom. As long as people are hardwired for connection, the fear of disconnection (aka shame) will always be a reality. ..Based on my work, I do believe that shame is still one of the most popular classroom management tools.”

Think about it.  When you talk to adults about their memories of school, and specifically math classrooms, many people will tell stories of being embarrassed or humiliated about getting something wrong, about feeling less than adequate or unworthy of being in the class they were in.  Even if the teacher was not doing anything deliberate, if a student has the courage to answer a teacher initiated question and get it wrong, the response that is given can make or break their self-worth that day.

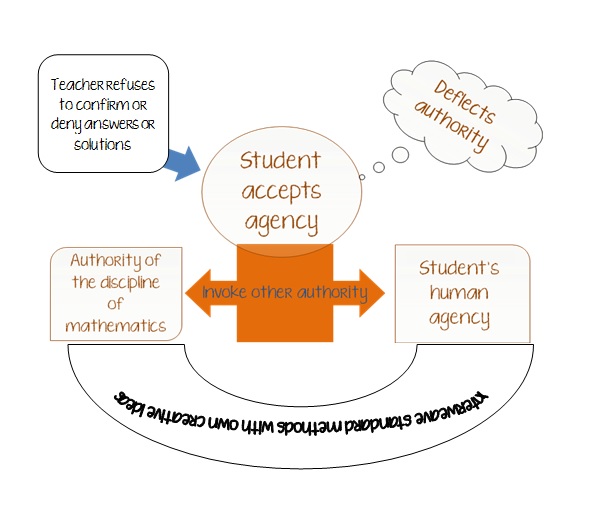
I’ve been giving this a lot of thought in the context of the PBL Classroom – How are we supposed to be teaching students how to take risks and not be afraid to be wrong and make mistakes in their learning if they have this fear of shame that is so deeply entrenched in our culture?  Especially in mathematics classrooms, how are we supposed to undo so many negative experiences that may have affected a student’s ability to allow themselves to be vulnerable and learn in this way?

PBL relies on the fact that a student is willing and able to make connections and conjecture regularly – numerous times in a class and on their own during “homework” time.  Being wrong and uncertain is really the norm and not the anomaly in this classroom.  As October rolls around and I hear more from students (and parents) about the discomfort they are feeling, I really do understand how different this is for everyone.  However, I do think we need to rely on the fact that students can be resilient and strong when pushed to try new things and to learn in a way that is good for them.  It is just that resilience that will make them better leaders, learners and more creative in the work force later on in life.

In talking to some students recently, I asked them where they thought they would learn more, in a classroom where it was laid out for them what they had to do or where they had to make choices about methods and sometimes it would be unclear.  I could tell that one girl was really struggling with that question.  She knew that it would be easier in the other classroom, but also knew that she would learn more and wanted to stay where her learning would be more effective.

What can I do to help this process go more smoothly?  Make sure that they know that I am working hard NOT to use shame as a classroom management tool.  That I am sincerely interested in the mistakes that they are making and how it is helping their learning.  I want them to grow from their errors and misconceptions and find ways to use those to their advantage.  I want to add to their self-worth not only as a math student, but as a problem solver in every way.

As Brene Brown says:

“I don’t believe shame-free exists but I do believe shame-resilience exists and that there are teachers creating worthiness-validating, daring classrooms every single today.”

I can be truly aware of the language that I use and the questions that I ask in order to make sure that everyone’s voice is heard and that my students know that I want to hear their ideas.  It’s really the only way to get them to Dare Greatly!

PS – Check out the wonderful quote by Teddy Roosevelt that I use in my PBL classes about Daring Greatly that Brene Brown used for the title of her book.

Get Comfortable with Uncertainty: A Short Dialogue

And so it begins.   The students are flustered. The emails are coming at night.  The faces stare at me, scared to death.  Although I repeat numerous times, “You do not have to come to class with each problem done and correct” students are totally freaking out about the fact that they can’t “do their homework” or they can’t “get” a certain problem on the homework.  No matter how many times I attempt to send the message the first few weeks about how unnecessary it is to come to class with a problem complete or an answer to show, students feel the need.

Tomorrow I am writing on my large post-it notes in HUGE capital letters, “Get comfortable with uncertainty because it’s not going anywhere.”  Every year about this time, I give the speech about how my homework is extremely different from any homework they have probably encountered in math class.  These are not problems that you are supposed to read, recognize and repeat.  They are there to motivate your thinking, stimulate your brain and trigger prior knowledge.  In other words,  you need to be patient with yourself and truly create mathematics.

Today I met with a young woman who I thought was about to cry.  She came and said, “I can’t do this problem that was assigned for tomorrow.”  Here’s how the conversation went:

Me: Why don’t you read the problem for me?

Girl:  Find points on the line y=2 that are 13 units from the point (2,14)

Me:  Ok, so show me what you did. (she takes out her graph paper notebook and shows that she graphed the line y=2, plotted the point (2,14)).  Great, that’s a great diagram.

Girl:  But it didn’t make sense because in order for it to be 13 units away, it had to be like, diagonal.

Me: Huh, what would that look like?

Girl: (drawing on her diagram) There’d be like two of them here and here.

Me; yeah?

Girl: But it can’t be like that….

Me: yeah? Why not?

Girl: Um…cause it wouldn’t be a straight distance.  I think..

Me: Is it 13 units away from (2,14)?

Girl: yeah, I think so…

Me: Hmmm….how far is (2,14) from the line y=2?

Girl:  Oh that’s easier – it’s like 12. ..Oh My gosh..it’s like a hypotenuse….and the other side that I don’t know is like the a and the 12 is like the b.  I can just find it.  Oh my gosh that’s so easy.  And the other one is on the other side.    Why didn’t I see that?

Me:  Well, you did…actually….

Girl: well, after you asked me that question…

Me: yeah, but eventually you’ll learn how to ask yourself those questions.

 

And they do….it’s just the beginning of the year.  We have to give them time – time to look into their prior knowledge as a habit, time to surprise themselves, time to have those moments, time to enjoy the moment and revel in the joy and courage and disappointment.  It’s all a part of the breakthrough that is needed to realize that they are creative and mathematics needs them to be.  It’s amazing and it’s worth it.

A New Year…Now What Do You Do?

OK, Carmel, enough with the summer of blogging about all this theory and ideas about teaching.  School is starting, we’ve committed to teaching with PBL – ack, things are starting to come into focus, huh?  I’m getting all these emails with questions about writing journals and dealing with parents and how to put things into action.  I’m right there with you guys….it’s Saturday and I’m having a workshop with two of my colleagues who have dedicated their time this year to teaching Geometry with me and PBL for the first time.  I’m so excited!

So I’ve put together a few documents that I think might be helpful.  The first one I’m posting here: Advice for Students Transitioning to PBL

This document is a list of quotes from actual students from years of teaching with PBL.  You can give it out if you like – maybe not on the first day, but after a few weeks – once your kids can relate.  I had kids at the end of the year write down advice to students at the beginning of the year, so that they would know how they will eventually feel.  That in the end, they will know that it’s worth it.  It’s actually kind of helpful for students to know that all of their hard work pays off.

The second document I also have posted under Metacognitive Journaling – it is a sheet that I give out about journaling and explains my expectations to students.  If you are considering assigning journals and having students use journals, this might be a good place to start for you.Keeping a Journal for Math Class

I also have written up a sheet that I call Teacher Cheat Sheet on PBL which includes some talking points for you to use when (maybe I should say “if”) you get resistance from parents.  I believe I also have an old blogpost about talking to parents too.  The initial first few months of using PBL is often very difficult, especially if your school had a traditional curriculum.  Please feel free to contact me for advice or feedback.  Honestly, what I have found most helpful is a very supportive administration and department chair and allowing parents to come and observe classes.  Don’t be nervous, because once they see that real mathematics is going on in the classroom, they become more confident in the learning.  Of course, the teachers need to feel confident in the learning process themselves before you allow the observations, but once they feel the culture of the classroom has meshed it should be fine.

Please feel free to get in touch if you have questions during this transition period and also remember that I do school visits.  Have a great beginning of the year!

Teaching Students to Become Better “Dancers”

So the other day I read a tweet by Justin Lanier that really sparked my interest.

 We all know the scenario in classroom discourse where a student asks a question – a really great question – and you know the answer, but you hedge and you say something like, “That’s a great question! I wonder what would happen if…”  So you reflect it back to the students so that they have something to think about for a little while longer, or maybe even ask a question like “Why would it be that way?” or “Why did you think or it like that?”  to try to get the student to think a bit more.  But what Justin, and the person who coined the phrase “authentic unhelpfulness” Jasmine Walker (@jaz_math), I believe were talking about was hedging because you really don’t know the answer – sincere interest in the uniqueness of the question – not because you’re so excited that student has helped you move the conversation forward, but because of your own excitement about the possibilities of the problem solving or the extension of the mathematics.

I think what got me so excited about this idea was how it connected to something that I was discussing earlier this summer with a group of teachers in my scaffolding in PBL workshop in late June.  In a PBL curriculum, the need to make sure that students have the right balance of scaffolded problems and their own agency is part of what Jo Boaler called the “Dance of Agency” in a paper she wrote in 2005 (see reference).  My understanding of this balance goes something like this:

(c) Schettino 2013

So initially, the student is confused (or frustrated) that the teacher refuses to answer the question although you are giving lots of support, advice and encouragement to follow their instincts.  The student has no choice but to accept the agency for his or her learning at that point because the teacher is not moving forward with any information.  But at that point usually what happens is that a student doesn’t feel like she has the authority (mathematical or otherwise) to be the agent of her own learning, so she deflects the authority to some other place.  She looks around in the classroom and uses her resources to invoke some other form of authority in problem solving.  What are her choices?

She’s got the discipline of mathematics – all of her prior knowledge from past experiences, she’s got textbooks, the Internet, her peers who know some math, other problems that the class has just done perhaps that she might be able to connect to the question at hand with previous methods that she might or might know how they work or when they were relevant – that discipline has had ways in which it has worked for her in the past and lots of resources that can help even if it may not be immediately obvious.

But she’s also got her own human agency which is most often expressed in the form of asking questions, seeing connections, drawing conclusions, thinking of new ideas, finding similarities and differences between experiences and thinking about what is relevant and what is not.  These pieces of the puzzle are not only important but a truly necessary function of the “dance of agency” and imperative to problem solving.

Interweaving both of these types of agency (and teaching kids to do this) have become more important than ever.  Yes, being able to use mathematical procedures is still important, but more important is the skill for students to be able to apply their own human agency to problem and know how and when to use which mathematical procedure, right?  This “dance” is so much more important to have every day in the classroom and if what initiates it is that deflection of authority then by all means deflect away – but the more we can “dance” with them, with “authentic unhelpfulness” and sincere deflection because we need to practice our own human agency, the more we are creating a true community of practice.

Boaler, J. (2005). Studying and Capturing the complexity of practice – the Case of the ‘Dance of Agency’

So How Do We Shift Gears?

OK, OK, I get the idea – not everything on the Internet is true and, for sure, not everything on the Internet is meaningful or helpful.  Since April of this year I have started following a bunch of people on Twitter (before that I really didn’t even know what it was or care) and thought that there were so many people out there that I wanted to learn from.  I would read other people’s blogs and try my best to think about what I had to learn from others. Mind you, I know I am definitely not the god of teaching, that’s for sure, but many of the things that are written out there – should I guess – with the hope of being “inspirational” or meaningful to others, I find less than helpful.

One site that I have really enjoyed reading which often has some great links and blogposts is Mindshift.  But they just tweeted this blog entry that cited an article about creating a business that fosters creativity.  OK, I see the connection to education, but honestly, it is a very different machine.  Kids and adolescents have a very different mindset than adults who are out there making money.  Not to mention the consequences of risk-taking in the classroom vs. risk-taking in the office have the potential for being very different.  (Assessment for grades has a different meaning possibly for a 13-year-old mind than brainstorming on the job, vs. assessment for a salary raise, etc for an adult who we hope can handle the pressure a little more.)

Then the blogger writes two short paragraphs at the end about how schools are just “incurious and risk averse” places.  Basically stating that schools don’t ever allow students to practice risk-taking or mistake making at all:

“Too few schools are incubators of curious and creative learners given their cultures of standardization, fear, and tradition. No doubt, external pressures exist that drive that culture. But if there ever was a time to shift gears, this is it. “

No doubt…sadly, our blogger, Will Richardson doesn’t really give us any advice on what to do about it….except, to do something about it. (Admittedly, he may have written something someplace else that I missed.)  And I don’t want to single out Mr. Richardson – I find tweets and blogs like this all day long – “Exploration, inquiry & problem solving are powerful learning mechanisms…” or “asking good questions and promoting discourse is an integral part of teaching and learning”…. Hmmm, well let me think about ways in which we can talk to teachers  in terms of mistake making and risk-taking:

  • Blogpost on making mistakes and classroom activity tied to Kathryn Schultz’ TED talk On Being Wrong
  • Discussion about article “Wrong is not always bad” with teachers
  • Modeling risk-taking in Problem-Solving in my course at ASG conference in June
  • Discussion of Relational Pedagogy to foster Risk-taking
  • Using a PBL curriculum to foster mistake-making and communication

I found that many teachers that I work with and who contact me are entirely dedicated to changing the culture of the mathematics classroom in the U.S. and making it (as Mr. Richardson writes) an “incubator of curious and creative learners.”  We need to make changes to our curriculum, our classroom relationships, our classroom culture and the authoritarian hierarchy that traditionally is prevalent in our mathematics classroom.  Students need to be able to feel safe enough, from judgment, alienation and failure to make those mistakes while learning.  We, as teachers, need to begin the discussion with each other about how to move forward with these initiatives and make sure that student voice is heard in the mathematics classroom as they question each other and us, the teachers, with true questions – ones we may not be able to answer.  These are the important aspects of creating curious learners who make mistakes and learn from them.  But we, as the adults in the room have a responsibility to let them feel safe in doing that.

I think teachers are aware of the fact that it’s time to “shift gears” – to make the classroom more conducive to students working together and taking chances.  There are so many subtleties to making this shift, however.  Students who need to shift, parents who are not used to that, assessment changes to be made – the list goes on and on.  I am doing what I can to help people with this conversation.  The pedagogy of relation (I believe) is at the heart of all of this – keeping in mind that in order for people to be vulnerable and make mistakes, we need to consider the interhuman aspect of learning.  In a classroom where this connection has for too long been typically so acceptably removed, it will take a lot of work to make this big “gear shift” but I’m up to it – bring it on!

Linking Theory to Practice: A Shout-Out to ‘savedabol’

This past January, I gave a key-note address at the ISOMA conference in Toronto and posted my slides from that talk on my academia.edu site that I thought would be a good place for me to easily give other people access to my work. (along with my website).  Academia.edu is great because it gives you lots of information about the stats of surfers who come and look at your information.  All of a sudden I saw that this powerpoint had more than something like 400 views and I couldn’t believe it.  I had to see who was searching and looking at this slideshow.

I quickly realized that someone had seen it, liked it and posted something about it on reddit.  There were only a few comments but one of them went something like this:

“I think the single worst part of being a teacher is sitting through PowerPoints like this, while some earnest non-classroom pedagogue tells us the bleeding obvious.”

Whooo – that one stung…my first instinct was to try and find out who that person was and defend myself to the ends of the earth.  Anyone who calls me a non-classroom pedagogue deserves to be righted…but then I kept reading…and someone with the alias ‘savedabol’ wrote this:

‘Carmel Schettino (the author) led a seminar I took at the Exeter math conference last summer. She is incredible. I can assure you that she is not a non-classroom pedagogue. She has been in the classroom nonstop for at least 20 years (that I know of). She is particularly scholarly when it comes to PBL and other ed topics, but that doesn’t make her irrelevant to what we do every day. Near the end she gives some great resources.’

I can’t tell you how affirmed I felt by ‘savedabol’ and I want to just let them know how nice that was of them to share their thoughts about my work with them.  I have been in the classroom non-stop since 1990 (except for two terms of maternity leave and one term of a sabbatical when I was a full-time student myself) and I pride myself in researching as much as possible about what I do.

I do wish that the first poster had had the chance to hear me speak instead of jumping to the conclusions they had – and it definitely got me thinking about something that was discussed last year at the PME-NA conference in October 2012.  I was one of maybe just a few people in the special category of math teacher/educator/researcher/doctoral students at this research conference where many of the math research folks were talking about ways in which they could breach the great divide of the theory people (them) and the practice people (us).

For many years I have lived this double life of both theory and practice and I have to say, I love it.  Having just finished up my Ph.D. and teaching full time was probably one of the toughest things I’ve had to do in my life, but having my mind constantly in both arenas has only helped me be a better teacher and a better researcher.

Jo Boaler is a great researcher at Stanford University who is doing great work in outreach between theory and practice this summer by offering a free online course called “How to Learn Math.”  It’s a course for k-12 teachers that is grounded in the most recent research in math education.  What a great idea!  She is sharing some of her wisdom freely online with k-12 teachers who want to spend some time learning about new ideas themselves.  I know I’m in.

In August 2008, the NCTM put together a special Research Agenda Project to work on recommendations for just this cause and you can see their report here.  One of the major recommendations that came out of their work was to not only emphasize the need for communication between researchers and practitioners, but in my view to help them realize that this communication would benefit both parties equally.  We all have something to share with each other and I know that I appreciate every classroom practitioners’ experiences.  I learn something from every teacher that ends up in my workshop every summer and often end up using many of their ideas as they do mine.

So let’s keep supporting each other both in real life and virtually, and realize that often times, the “bleeding obvious” is something that needs to be stated and discussed over and over again to be sure that we are still talking about it with the right people.

PBL – Students making Mathematical Connections

As someone who has used Problem-Based Learning for almost 20 years and sad to say has never been part of a full-fledged Project-Based Learning curriculum, what I know best is what I call PBL (Problem-Based Learning).  I know there is a lot of confusion out there is the blogosphere about what is what, and with which acronyms people use for each type of curriculum.  I did see that some people have been trying to use PrBL for one and PBL for the other, but I guess I don’t see how that clarifies – sorry.

So when I use the acronym PBL in my writing I mean Problem-Based Learning and my definition of Problem-Based Learning is very specific because it not only implies a type of curriculum but an intentional relational pedagogy that I believe is needed to support learning:

Problem-Based Learning (Schettino, 2011) – An approach to curriculum and pedagogy where student learning and content material are (co)-constructed by students and teachers through mostly contextually-based problems in a discussion-based classroom where student voice, experience, and prior knowledge are valued in a non-hierarchical environment utilizing a relational pedagogy.

Educational Psychologist and Cognitive Psychologists like Hmelo-Silver at Rutgers University have done a lot of research on how students learn through this type of scaffolded problem-based curriculum dependent on tapping into and accessing prior knowledge in order to move on and construct new knowledge.  There was a great pair of articles back in 2006/2007 where Kirschner, Sweller & Clark spoke out against problem- and inquiry-based methods of instruction and Hmelo, Duncan and Chinn responded in favor.  I highly recommend reading these research reports for anyone who is thinking of using PBL or any type of inquiry-based instruction (in math or any discipline).  It really helps you to understand the pros and cons and parent and administrator concerns.

However, after you are prepared and know the score, teachers always go back to their gut and know what works for their intuitive feeling on student learning as well.  For me, in PBL, I look at how their prior knowledge connects with how, why and what they are currently learning.  One of the best examples of this for me is a sequence of problems in the curriculum that I use which is an adaption from the Phillips Exeter Academy Math 2 materials.  I’ve added a few more scaffolding problems (see revised materials) in there in order to make some of the topics a bit fuller, but they did a wonderful job (which I was lucky enough to help with)and keep adding and editing every year. The sequence starts with a problem that could be any circumcenter problem in any textbook where students use their prior knowledge of how to find a circumcenter using perpendicular bisectors.

“Find the center of the circumscribed circle of the triangle with vertices (3,1), (1,3) and (-1,-3).”

Students can actually use any method they like – they can use the old reliable algebra by finding midpoints, opposite reciprocal slopes and write equations of lines and find the intersection points.  However, I’ve had some students just plot the points on GeoGebra and use the circumcenter tool.  The point of this problem is for them to just review the idea and recall what makes it the circumcenter.  In the discussion of this problem at least one students (usually more than one) notices that the triangle is a right triangle and says something like “oh yeah, when we did this before we said that when it’s an acute triangle the circumcenter is inside and when it’s an obtuse triangle the circumcenter is outside.  But when it’s a right triangle, the circumcenter is on the hypotenuse.”

Of course then the kid of did the problem on geogebra will say something like, “well it’s not just on the hypotenuse it’s at the midpoint.”

 

Dicussion will ensue about how we proved that the circumcenter of a right triangle has to be at the midpoint of the hypotenuse.

A day or so later, maybe on the next page there will be a problem that says something like

“Find the radius of the smallest circle that surrounds a 5 by 12 rectangle?”

Here the kids are puzzled because there is no mention of a circumcenter or triangle or coordinates, but many kids start by drawing a picture and thinking out loud about putting a circle around the rectangle and seeing they can find out how small a circle they can make and where the radius would be.  When working together oftentimes a student see a right triangle in the rectangle and makes the connection with the circumcenter.

A further scaffolded problem then follows:

“The line y=x+2 intersects the circle  in two points.  Call the third quadrant point R and the first quadrant point E and find their coordinates.  Let D be the point where the line through R and the center of the circle intersects the circle again.  The chord DR is an example of a diameter.   Show that RED is a right triangle.”

Inevitably students use their prior knowledge of opposite reciprocal slope or the Pythagorean theorem.  However, there may be one or two students who remember the circumcenter concept and say, “Hey the center of the circle is on one of the sides of the triangle.  Doesn’t that mean that it has to be a right triangle?”  and the creates quite a stir (and an awesome “light bulb” affect if I may say so myself).

A few pages later, we discuss what I like to call the “Star Trek Theorem” a.k.a. the Inscribed angle theorem (I have a little extra affection for those kids who know right away why I call it the Star Trek Theorem…)

I will always attempt to revisit the “RED” triangle problem after we discuss this theorem.  If I’m lucky a student will notice and say, “Hey that’s another reason it’s a right triangle – that angle opens up to a 180 degree arc, so it has to be 90.”  and then some kid will say “whoa, there’s so many reasons why that triangle has to be a right triangle”  and I will usually ask something like, “yeah, which one do you like the best?” and we’ll have a great debate about which of the justifications of why a triangle inscribed in a circle with a side that’s a diameter has to be right.  So who are the bigger geeks, their teacher who names a theorem after Star Trek or them?

References:

Kirschner, P. A., Sweller, J., & Clark, R. E. (2006). Why minimal guidance during instruction does not work: An analysis of the failure of constructivist, discovery, problem-based, experiential and inquiry-based teaching. Educational Psychologist, 41(2), 75-86.

 

Hmelo, C. E., Duncan., R.G., & Chinn, C. A. (2007). Scaffolding and achievement in problem-based and inquiry learning: A response to Kirschner, Sweller and Clark (2006). Educational Psychologist, 42(2), 99-107.

 

Creating a Conspiracy in the PBL Classroom

Any Mad Men fans out there?  I just love some of the characters and the struggles they put themselves through.  In one episode from season 5, called “Signal 30,” Lane Pryce needs to take some clients out to dinner and Roger Sterling is giving him some advice on how to woo them to sign a contract with Sterling Cooper Draper Pryce.  Since he is not an account man, Lane is nervous about landing the account.

Roger:  And then it’s kind of like being on a date.

Lane:  Flattery, I suppose…

Roger:  Within reason, but I find it best to smile and sit there like you’ve got no place to go and just let ‘em talk.  Somewhere in the middle of the entrée, they’ll throw out something revealing and you want to wait ‘til dessert to pounce on it. You know, let him know you’ve got the same problem he has.  Whatever it is, and then you’re in a conspiracy – the basis of a quote “friendship”.  Then you whip out the form.

Lane:  What if I don’t have the same problem?

Roger:  It’ll probably be something like he drinks too much, he gambles…I once went on a five minute tear about how my mother loved my father more than me and I can assure you, that’s impossible.

Lane:  Very good then, and if for some reason he’s more reserved?

Roger:  You just reverse it – feed him your own personal morsel.

Lane:  Oh I see.

Roger: (getting up to leave) That’s it, get your answers, be nice to the waiter and don’t let him near the check.

My husband and I watched this episode about the same time I was having a great deal of resistance in my class to PBL.  I was talking to my husband about how to get students to buy into the notion of learning for the sake of learning where everywhere else in their lives what measures their learning are their grades.  Why would I expect anything different from them if this is the culture they were brought up in?  They depend on their grades to get them into a good college and if their grades are not up to a certain standard, they will not “measure up.”

I get this question all the time from other teachers – about  how to motivate students to find the love of learning and the interest in problems when they do not necessary know the solution methods to find them.  I usually tell them the same things – talking about the values of the class, grading class contribution with a viewable rubric,  grading their metacognitive journal writing, rewarding them with an interesting relationship with a great teacher…OK that might be pushing it.

However, this year is different.  I am having the hardest time trying to let them know what I want from them.  They do the homework, try their best, write down notes, but for some reason it feels different.  It’s almost as if there’s this wall between them and me and I don’t know how to get them to see my side.  I have had this problem with students in the past, but usually with a whole class.  Some of them blatantly are interrupting each other and others are obviously ignoring each other.

Then my husband says, “Maybe it’s like the conspiracy.”  I said, “What?” He said,” You know, what Roger was talking about on Mad Men.  Now, Roger Sterling is no saint (those of you who watch the show know this all too well) and I usually take what he says with a grain of salt.  I also would not ever consider taking advice from him, especially about teaching, but I allowed my husband to continue.  He said maybe what I had to do was build up the conspiracy that Roger was talking about.  I had a real problem with that because I am so committed to relational pedagogy that there’s no way I could lie to or mislead a student about their learning.  But that’s not what he really meant.

I suddenly realized that what had happened was I was teaching a curriculum that I didn’t even buy into.  I had just finished teaching them matrices and matrix operations with some problems that I had written, and it went very well.  However, in the end I did have to do Cramer’s Rule and determinants.  I tried motivating the problems about determinants with the area of a parallelogram, which kept them interested for a while, but in the end, with a 3×3 it was just here’s the way to do it.  I’m not sure that I could’ve expected them to have enough prior knowledge to derive the formula for finding a determinant of a 3×3.  As much as I tried to cover it up with problem-based learning, it was still a curriculum that is antiquated and not necessarily what I felt they should be doing and learning.  I couldn’t hide it any longer.

But we’re caught aren’t we?  Do we change the whole system – college prep curriculum, SAT required math, college expectations – and if so how do we do that? (see ahbel.com for a great article on this and a keynote address called Reflections on a 119 year old curricullum!)  Do we move beyond the required standardized testing material and allow our students to see mathematics the way we see it?  Yes, that’s the conspiracy – that’s what my husband was talking about.  When kids complain to me, I will “smile and sit there while they talk” knowing that I’m going to try to get something that we have in common.  “Do you hate solving a system of three equations with three unknowns with a determinant? Oh yeah, I did too in high school.  Wouldn’t it be great if we could do something else?  What else should we do?  Let me find some other problems that might be interesting.”  We have the same problem (literally and figuratively), now we’re on the same playing field having similar motivating factors.

And you know what?  I don’t think it would be the end of the world if they’re not revealing and you reversed it.  We are allowed to say to them that we don’t understand why we are still teaching this and these would be my reasons for taking it out of the curriculum – part of your own personal morsel.  It might actually bring you closer as a class and have you talking about how your hands are tied and we have to get through this “together.”

Yeah, there are little tricks that can be learned and carrots that can be used to get students to do what you want them to do, but in PBL, that’s not the point.  There is very little for them to mimic because it is based on their prior knowledge.  They are the ones who need to move the curriculum forward.  So in a nutshell,

  1. Take action – Get to problems in order for students to start feeling empowered and active in class.  Once they see that they are capable of a great deal on their own, it is amazing what they can accomplish.
  2. Create relationships – be sure that you are being reciprocal in your attempts at problems and valuing theirs.  The concept of Relational Trust and Authority are huge parts of a PBL pedagogy (Boaler, Bingham)
  3. But make sure that you are at least somewhat in control in the end because we are, at least for now, still responsible for making sure that some understanding of what we might consider unnecessary skills, for their next courses or future use.

As Roger said, “Get your answers, be nice to the waiter and don’t let ‘em near the check.”  Create that conspiracy.

 

 

 

Defying Gravity as a Means to Learning from Mistakes

There’s a lot of blogging, writing and research (and anecdotal stories) out there these days about trying to foster the value in students for the appreciation in failing.   I even wrote a blog entry two years ago entitled “modeling proper mistake-making” way before I read anything or watched any videos on the Internet.  From teaching with PBL for over 17 years, I am a pro at making mistakes and watching students struggle with the concept of accepting the idea of learning from their mistakes.  This is so much easier said than done, but it is clearly something that grow to love even if only for a short time.

Last April, I had the pleasure of hearing Ed Burger at the NCTM national conference where he spoke about having students in his college-level classes required to fail before they could earn an A in his class.  In his August 2012 essay “Teaching to Fail” from Inside Higher Ed (posted at 3:00 am, which I thought was kind of funny), he talks about attempting to make a rubric for the “quality of failure” on how well a student had failed at a task.  I thought this was an interesting concept.  I mean, in order to fail well, can’t you just really screw up, like not do it at all?  Prof. Burger states that allowing students to freely reflect on their “false starts and fruitful iterations” as well as how their understanding “evolved through the failures” can be extremely beneficial.  He also states:

“To my skeptical colleagues who wonder if this grading scheme can be exploited as a loophole to reward unprepared students, I remind them that we should not create policies in the academy that police students, instead we should create policies that add pedagogical value and create educational opportunity.”

Last year for the first time, I tried a similar experiment wherein I gave students an assignment to write a paper in my honors geometry class.  They had to choose from three theorems that we were not going to prove in class.  However, it was clear that they could obviously just look up the proof on the Internet or in a textbook or somewhere, since they clearly have been proven before.  The proof was only 10 or 20% of their grade.  The majority of the paper’s grade was writing up the trials and failures in writing the proof themselves.  This proved to be one of the most exciting projects of the year and the students ate it up.  I even told them that I didn’t care if they looked up the proof as long as they cited it, but I still had kids coming to me to show my how they were failing because they wanted a hint in order to figure it out themselves.  It was amazing.

This past week I showed my classes Kathryn Schultz’ TED talk entitled “On Being Wrong” in which she talked about the ever popular dilemma of the Coyote who chases the Road Runner, usually off a cliff.

My students loved her analogy of the “feeling of being wrong” to when the Coyote runs off the cliff and then looks down and of course, has to fall in order to be in agreement with the laws of gravity.  However, I proposed a different imaginary circumstance.  Wouldn’t it be great if we could run off the cliff, i.e. take that risk, and before looking down and realizing that vulnerability and scariness, just run right back on and do something else?  No falling, no one gets hurt, no one looks stupid because you get flattened when you hit the ground?  Maybe that’s not the “feeling of being wrong” but it’s the “feeling of learning.”

Next blog entry on creating the classroom culture for “defying gravity.”

The Role of Technology in Relational Pedagogy?

So I’ve been thinking a lot lately about technology and learning.  There’s so much in the news about MOOCs, using iPads, schools using technology, etc.  I am even part of a pilot program at my school right now where all of my students have iPads in my honors geometry class and we are trying to communicate at night using Voicethread and the iPads.  My hope was that having a way to share ideas during the evening would lessen the stress of homework problems that students are asked to grapple with in the PBL curriculum would give them more opportunities to throw out problem-solving ideas with each other before class starts so that we would spend less time in class debating different methods of solving the problem (although that’s what I love about class, right?).

But I’m asked as a teacher to find ways to integrate technology into my classroom – but to what end?  I want to find ways to use technology to solve problems, to explore ideas and to help improve students’ understanding of the mathematics.  Not necessarily help them communicate with each other, which is what I’m finding most of the apps out there are for right now – which I am open to – but they are removing a huge part of the learning triangle.  In fact, David Hawkins (1974) wrote about the I-thou-it reciprocal relationships in learning that simply must exist between the learner, the teacher and the subject matter.  He said that if one of the relationships is hindered or dysfunctional in some way, that learning is not optimal.

Hawkins (1974)

So if I interrupt that relational triangle between the students’ communication with the material (and with each other) and with me, using technology instead of discussion and the connection with all three, my fear is that learning is not optimal.  Perhaps the technology could enhance it, but for now I see that it is not truly happening.  My guess is that it has to take time for the students maybe to want for that to happen.

I also just read an article on Edutopia by a guy named Matt Levinson that was entitled “Where MOOCs Miss the Mark: The Student-Teacher Relationship” where it was stated that a lack of mentorship, close guidance or meaningful relationship between teachers and students is what is really lacking in these online courses. Even students who use Khan Academy lectures for “learning” sometimes comment that even though they don’t like sitting and listening to lectures in math class, they would “much [prefer] listening to her math teacher explain the same concepts because she likes this teacher and feels comfortable asking questions and going for extra help outside of class.”

Carol Rodgers (one of my most favorite people on earth) writes about teacher presence and the importance of it in the classroom.  I believe in mathematics class and especially the problem-based mathematics class it is truly essential because in order for students to take a risk with a method, they need to feel supported and safe in order to be open to new ideas and to discuss them with others.  With the open presence of a teacher and mentor, students are not “receiving knowledge” but creating it with others – creating it within those relationships that Hawkins was talking about – maybe with technology or without it.  But  for someone who just spent two years writing about the importance of relational pedagogy in PBL, I find it extremely difficult to assume that without those relationship the same exceptional amount of learning would go on.