Category: In the classroom

Yours, Mine and Ours

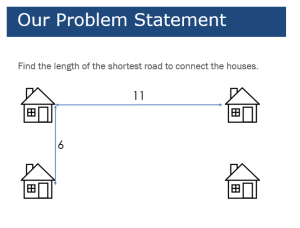
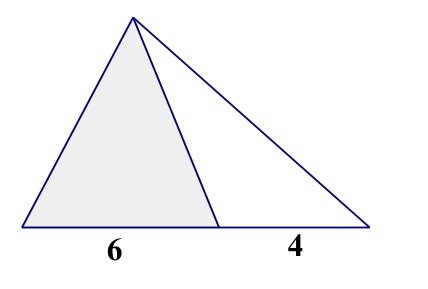
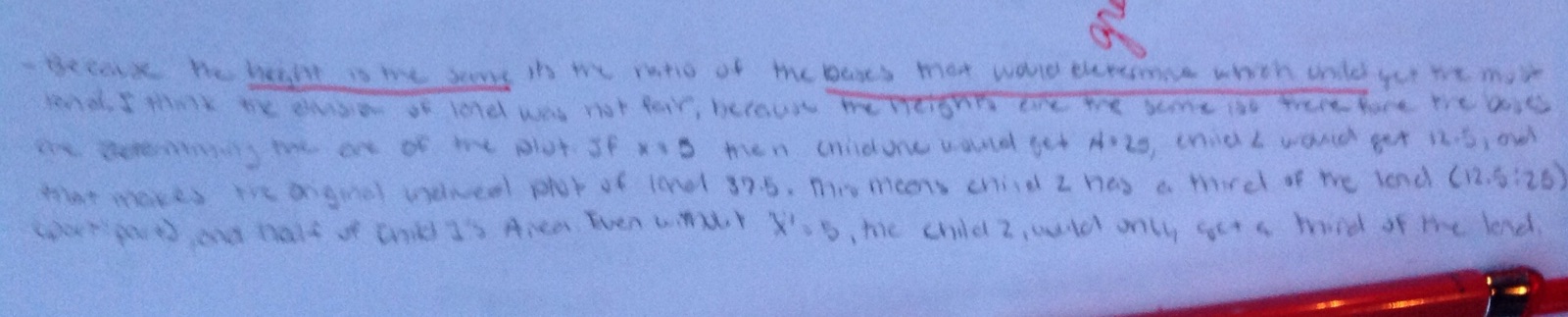Yesterday we had a speaker in our faculty meeting who came to talk to us about decision-making process in our school.  He spoke about the way some colleges, universities, independent schools are very different from businesses, the military, and other governing bodies that have to make decisions because we are made up of “loosely-coupled systems.” These are relationships that are not well-defined and don’t necessarily have a “chain of command” or know where the top or bottom may be.  They also don’t necessarily have a “go-to” person where, when a problem arises, the solution resides in that location.  The speaker said that this actually allows for more creativity and generally more interesting solution methods.

About mid-way through his presentation he said something that just resonated with me fully as he was talking about the way these systems come to a decision cooperatively.

“The difference between mine and ours is the difference between the absence and presence of process.”

Wow, I thought, he’s talking about PBL.  Right here in faculty meeting.  I wonder if anyone else can see this.  He’s talking about the difference between ownership of knowledge in PBL and the passive acceptance of the material in a direct instruction classroom.

Part of my own research had to do with how girls felt empowered by the ownership that occurred through the process of sharing ideas, becoming a community of learners and allowing themselves to see others’ vulnerability in the risk-taking that occurred in the problem solving.  The presence of the process in the learning for these students was a huge part of their enjoyment, empowerment and increase in their own agency in learning.

I think it was Tim Rowland who wrote about pronoun use in mathematics class (I think Pimm originally called it the Mathematics Register). The idea of using the inclusive “our” instead of “your” might seem like a good idea, but instead students sometimes think that “our” implies the people who wrote the textbook, or the “our” who are the people who are allowed to use mathematics – not “your” the actual kids in the room.  If the kids use “our” then they are including themselves.  If the teacher is talking, the teacher should talk about the mathematics like the are including the students with “your” or including the students and the teacher with “our”, but making sure to use “our” by making a hand gesture around the classroom.  These might seem like silly actions, but could really make a difference in the process.

Anyway,  I really liked that quote and made me feel like somehow making the process present was validated in a huge way!

End of Term Reflections

7 Comments

Phew…exams given…check…exams graded…check…comments written…check…kids on bus…check.  Now I can relax.  Oh wait, don’t I leave tomorrow to drive to my sister’s for Thanksgiving?

Such is the life of a teacher, no?  Just when you think you are on “vacation” there’s always something else to do.  I had an exam on Saturday then worked the rest of Saturday and Sunday finishing up that grading and writing my comments that were due this morning at 9 am.  But wait, I told some people I would write a blogpost about what my classroom is like, so I really wanted to do that too.  That’s OK though, I think it’s important for me to reflect back on this fall term – what worked and what didn’t for my classes.

I have three sections of geometry this year that I teach with PBL and a calculus class that I would say is something of a hybrid because we do have a textbook (as an AP class I needed to do what the other teachers were doing), but I do many problems throughout the lessons.

In my geometry classes, the student have iPads on which they have GeoGebra, Desmos and Notability where they have a pdf of their text (the problems we use) and where they do all of their homework digitally.  My class period for that course alternate between small group discussions in the Innovation Classroom in the library on Mondays and Thursdays and whole class discussions with student presentations of partial solutions (a la Jo Boaler or Harkness) on Tuesdays and Fridays. (We meet four times a week 3 45-minute periods and 1 70-minute period.)  Because my curriculum is a whole-curriculum PBL model, we spend most of the time discussing the attempts that the students made at the problems from the night before.  However, in class the discussion centers around seeing what the prior knowledge was that the presenter brought to the problem and making sure they understood what the question was asking.

classroom-shot1
Whole Class Discussion in regular classroom

 

geom-class-2
Small Group Discussions in Innovation Lab

If this didn’t happen we end up hearing from others that can add to the discussion by asking clarifying questions or connecting the question to another problem we have done (see Student Analysis of Contribution sheet).

One of the things that I had noticed this fall in the whole class discussion was that the students were focusing more on if the student doing the presentation was right immediately as opposed to the quality or attributes of the solution method.  There was little curiosity about how they arrived at their solution, the process of problem solving or the process of using their prior knowledge.  Unfortunately, it took me a while to figure this pattern out and I felt that it had also weeded itself into the small group discussion as well.

One day in the small group discussions, it became clear to me that the students were just looking for the one student who had the “right” answer and they thought they were “done” with the question.  This spurred a huge conversation about what they were supposed to be doing in the conversation as a whole.  I felt totally irresponsible in my teaching and that I had not done a good enough job in describing to them the types of conversations they were supposed to be having.

This raised so many questions for me:

  1. How did I fail to communicate what the objectives of discussing the problems was to the students?
  2. Why is this class so different from classes in the past (even my current period 7 class)?
  3. How can I change this now at this point in the year?
  4. How can I stress the importance of valuing the multiple perspectives again when they didn’t hear it the first time?

In my experience, sometimes when students are moving forward with the fixed mindset of getting to the right answer and moving on, it is very difficult to change that to a more inquiry-valued mindset that allows them to see how understanding a problem or method from a different view (graphical vs algebraic for example) will actually be helpful for them.

My plan right now is to start the winter term with an interesting problem next Tuesday.

“A circular table is pushed into the corner of the room so that it touches both walls. A mark is made on the table that is exactly 18 inches from one wall and 25 inches from the other.  What is the radius of the table?”

table-picture-problem

I have done this problem for many years with students and I have found the it works best when they are in groups.  I usually give them the whole period to discuss it and I also give them this Problem Solving Framework that I adapted from Robert Kaplinsky’s wonderful one from his website.  I am hoping to have a discussion before they do this problem about listening to each other’s ideas in order to maximize their productivity time in class together.  We’ll see how it goes.

Modeling with Soap Bubbles

2 Comments

I am so very lucky to have a guest teacher with me this year at my school.  Maria Hernandez (from the North Carolina School of Science and Math) is probably one of the most energetic and knowledgeable teachers, speakers and mathematicians you could ever find – and we got her for the whole year!  We are so excited.  I am working with her and she is so much fun to work with.  I have been teaching calculus with PBL for almost 20 years now and thought I had all the fun I could but no!  Maria is bringing modeling into my curriculum and I’m enjoying every minute of it.

As we started teaching optimization this week, Maria had this wonderful idea that she had done before where we want to find the shortest path that connects four houses.

picture-of-houses

I let the kids play with this for about 10 minutes and then did this wonderful demonstration with some liquid soap bubbles and glycerin.  We had two pieces of plastic and four screws that represented the houses.  As the kids watched, I dipped the plastic frame into the liquid and voila-file_000

Right away the students saw what they were looking for in the shortest path.  Now they had to come up with the function and do some calculus. As they talked and worked in groups, It was clear that using a variable or one that would help them create the right function was not as easy as they thought.  However,  I was requiring them to write up what they were doing and find a solution so they were working hard.

file_000-1

We have been doing a lot of writing in Calculus this fall so far and they are getting used to being deliberate about their words and articulating their ideas in mathematical ways.

Here is the outline of the work they did in class: Shortest Path Lab

and here is the rubric that I will be using to grade it.

rubric-for-lab-3-2

The engagement of students and the buzz of the classroom was enough to let me know that this type of problem was interesting enough to them – more than the traditional “fold up the sides of the box.”  The experience they had in conjecturing, viewing, writing the algebra and solving with calculus was a true modeling experience.

If you decide to do this problem or have done something like it before, please share – I’d love to do more like this.  I am very lucky to have a live-in PD person with me this year and am grateful every day for Maria!

 

What is “Low Ability” Anyway? Comparing a Point to “Room”

One of my big “beefs” at my school is the fact that we have three levels of tracking – count ’em, three.  There’s the honors track, that of course at a college prep school, most kids think they belong in.  There’s the regular track, that which is still pretty quick and difficult, and there’s the track that the kids who are sometimes, I would say, just not very motivated to learn math, or have less interest in math, or maybe come from a school with a less rigorous math program, are placed in.  These are the kids who probably all their lives have been told they are not “math people” and have been pigeon-holed as an “artist” or “writer” so they won’t actually need math when they get older.  This really, really irks me.  But I do it – I go along with a system that has been in place way before I got here.  I’m only one person – even though I cite Jo Boaler’s list of research showing why “tracking” in general is just a bad idea and hurtful – I know I can’t win.

Anyway, I really shouldn’t complain because the department has let me do my thing with the geometry curriculum and I have written a PBL curriculum for the three levels.  In my 201 book, I have created scaffolded problems that I think work really well with these “low-abiity” kids and often challenge them enough to make them realize how much ability they actually have.  We just started talking about dimension and we watch these clips from Flatland: The Movie, where Arthur T. Square meets the King of Pointland and then meets the King of Lineland.

We had a great conversation about why the King of Pointland keeps saying “Hello Me, Hello Me” and can’t really understand why there’s anyone else there.  We talked about why the King of Lineland doesn’t understand where the Square is because he only understands the directions of left and right.  One of the kids goes, “Is this kind of like what happened in the movie Interstellar? I think he went through a black hole and just appeared in the future or something.” Now, I hadn’t seen that movie but then another kid said, “Well, I’m not sure it was like that.” But then one of the other students says, “No, the King of Pointland is kind of like the kid in the movie Room.  Did you see that movie?”  I nodded in understanding and so did many of the others in class. The student went on, “In Room, the little boy grew up thinking that “Room” was his whole universe so that was all he understood, and that’s why the King of Pointland seems so nuts. That point with no dimensions is all he can understand – there’s no one else in the world.”  I was so blown away by that analogy.  She really had an understanding of the idea of the limitations of being alone in the universe of a point. I had never had a kid in a “regular” or “honors” class make a connection like that – but then again, Room just came out!

Repost: Always Striving for the Perfect Pose

2 Comments

Back in 2010, I wrote an blogpost comparing teaching with PBL to doing yoga. Since I have been doing Bikram Yoga for almost a year now and still can’t do “standing head to knee pose” *at all* – I thought I would repost this one just to give myself some perspective, and possibly many of you out there who might need a little encouragement at this beginning of the year time. I know that every year when students begin a year in a PBL math class the obstacles return. Parents are questioning “why isn’t the teacher teaching?” Students are questioning “why is my homework taking so long?” Teachers new to the practice are questioning “When is this going to get easier?” and “why aren’t they seeing why this is good for them like I do?” The best thing to remember is that it is a process and to understand how truly different and hard it is for students who are used to a very traditional way of learning mathematics. Give them time, have patience for them and yourself and most of all reiterate all of what you value in their work – making mistakes, taking risks, their ideas (good and bad) and be true to the pedagogy.

Here’s the original blogpost I wrote:

I don’t think my professor, Carol Rodgers, would mind me borrowing her yoga metaphor and adapting it to PBL. I use it often when talking to teachers who are nervous about falling short of their ideal classroom situation or teaching behaviors. I think this can happen often, especially when learning best practices for a new technique like facilitating PBL. There are so many things to remember to try to practice at your best. Be cognizant of how much time you are talking, try to scaffold instead of tell, encourage student to student interaction, turn the questions back onto the students, etc. It really can be a bit overwhelming to expect yourself to live up to the ideal PBL facilitator.

However, it is at these times that I turn to Carol’s yoga metaphor. She says that in the practice of yoga there are all of these ideal poses that you are supposed to be able to attain. You strive to get your arms, legs and back in just the right position, just the right breathing rhythm, just the right posture. But in reality, that’s what you’re really doing – just trying. The ideal is this goal that you’re aiming for. Just like our ideal classroom. I go in everyday with the picture in my head of what I would want to happen – have the students construct the knowledge as a social community without hierarchy in the authority where everyone’s voice is heard. Does that happen for me every day? Heck no. I move the conversation in that direction, I do everything in my power for that to happen, but sometimes those poses just don’t come. Maybe I just wasn’t flexible enough that day, or maybe the students weren’t flexible enough, maybe we didn’t warm up enough, or the breathing wasn’t right. It just wasn’t meant to be. I have exercises to help me attain the goal and I get closer with experience. That’s all I can hope for.

So I tell my colleagues who are just starting out – give yourself a break, be happy for the days you do a nearly perfect downward facing dog, but be kind to yourself on the days when you just fall on your butt from tree pose. We are all just trying to reach that ideal, and we keep it in mind all the time.

Journals: Paper vs Digital: The Pros and Cons

5 Comments

I was totally honored the other day when I saw some tweets from TMC16 from @0mod3 and @Borschtwithanna

 

And yes it’s true, I’ve been writing and practicing the use of metacognitive journaling for very long time – probably since 1996 ever since I read Joan Countryman’s book about mathematical journaling and heard about it in many workshops that summer.  I wrote a rubric (make sure you scroll to the 3rd page) while I was at the Klingenstein Summer Institute for New Teachers (that’s how long ago it was) and since then I’ve been refining that rubric based on feedback from students and teachers. A few years ago, I finally refined a document called How to Keep a Journal for Math Class to a degree that I really like it now.  However, please know that lots of math teachers do journaling differently and without the metacognitive twist. I do believe that metacognitive writing is essential to the PBL classroom (read more here)

So this morning, I was asked this question on twitter

 

Which is something that many people often ask so I thought I’d respond with a more in-depth answer.

Here are the pros, I’ve found over the years of having students journal digitally:

Speed/complexity: Students are used to typing, using spell-check, inserting pictures, graphics and naturally including documents, links and thinking in the complex way that digital media allows them to.  It allows their journal to be more rich in content and sometimes connect problems to each other if their journal is say on a google doc that can connect to other html docs.  If they create, for example, iBooks or Explain Everything videos, there is even a lot more richness that can be embedded in the file as well – their creativity is endless.

Grading/Feedback: I found grading in Notability or on Google docs or some other digital platform really nice that allowed you to add comments with a click or audio extremely easy and quick.  I did not receive feedback from the students very often about how the feedback helped them though.  If you use an LMS like Canvas that integrates a rubric or integrates connection to Google it’s even nicer because you can have those grades go right from your assignment book to your gradebook.

I love having kids use digital platforms for writing/creating in mathematics when it is for a project or big problem that I want them to include many pieces of evidence, graphs, geogebra files and put it together nicely in a presentation or portfolio.  Not necessarily for their biweekly journals. Some guys who make use of digital journals in interesting ways are @GibsonEdu and @FrasiermathPBL at the Khabele School in Austin TX.

Here are the cons, in my mind of using digital journals: (which might be the “pros” of paper journals) – which is the side I have come down on.

the “real” writing factor: there is some research about the actual physical process of writing and the time it takes for kids to process their thoughts.  I do believe that when i want kids to be metacognitive about their learning and also want them to be thoughtful and take the time think about their initial error, think about what happened in class discussion to clear up their misunderstanding and also then what new understanding they came to.  That’s a lot of thinking. So I want them to take the time to write all that down.  Sometimes typing (like what I’m doing right now!) is a fast process and I’m not sure I do my best writing this way.

practice in hand-writing problem solving: this is re-enacting doing homework and sitting for assessments (in my class at least) and I want them to do this more regularly.  If in your class kids take assessments digitally or do homework nightly digitally then maybe they should do their journal digitally as well. This also give me practice in reading their handwriting, getting to hear their voice through their handwriting and seeing what it looks like on a regular basis.  In a time crunch on an assessment it honestly helps me know what they are thinking.

Conversational Feedback: I feel that when I hand write my feedback to them I can draw a smilely face or arrows or circle something that I want to emphasize more easily than when it is on something digitally (this is also true in a digital ink program – so that is something to consider, like Notability for example). I give feedback (see some journal examples on my blog) that is very specific about their writing and want the to improve not only in the math aspect of their writing but in how they are looking at their learning.  I want them to respond and I want to respond in the hope that we are starting a mathematical conversation about the problem.  I have received more questions about the feedback in the paper journals (like “what did you mean by this?”) than on the electronic feedback – not sure why.

Portability: I find that small composition graph paper notebook is extremely portable and easy for me to carry home to grade.  The students bring them to their assessments and there is nothing else in the notebook (no homework at all and no access to the internet) so I am not worried about academic honestly.

There are probably more but this is it in a nutshell – please add your comments below or tweet me to let me know your thoughts!

 

Adventures in Feedback Assessment

On an assessment students did for me today I gave this question:

An aging father left a triangular plot of land to his two children. When the children saw how the land was to be divided in two parts (Triangle ADC and Triangle BDC), one child felt that the division of the land was not fair, while the other was fine with it. What do you think and why? Support your justification with mathematical evidence.

 So this student had a hard time with this question. Since there was no height given and the bases were different, she was unable to think about how to compare the areas. She was however able to say that it would be a fair split if the areas were the same. So since I am doing this work this year with giving feedback first and then grades (see past blogpost “Why teachers don’t give feedback before grades and why they should”) I wrote this feedback on the problem set: 
 I am trying to get her to remember a problem we did in class where there was a similar problem we did with an acute triangle and obtuse triangle that shared the same height:

The area of the shaded triangle is 15. Find the area of the unshaded triangle.

This idea of where the height of obtuse triangles are is a really tough one for some geometry students. But more than that the idea of sharing a height and what effect that has on the area is also difficult.

We will see tomorrow if this student is able to take my feedback and see what whether the division of the land is fair.

By the way, here’s a response that another student had:


Just in case you can’t read it:

“Because the height is the same, it’s the ratio of the bases that would determine which child would get the most land. I think the division of land was not fair, because the heights are the same so therefore the bases are determining the area of the plot. If x=5 then child one would get A=20, child 2 would get 12.5 and that makes the original plot of land 37.5. This means child 2 has a third of the land (12.5:25) (part:part) and half of child 1’s) Even without x=5, the child 2 would only get a third of the land.”

We’ll see what happens!

Getting Kids to Drive the Learning

2 Comments

It doesn’t always work this way, but it would be awesome if it did.  When PBL is perfect or ideal, the students are the ones who make the natural connections or at least see the need or motivation for the problems that we are doing.  Yeah, some of them are just really interesting problems and the get pulled in by their own curiosity, but as all math teachers know, we have a responsibility to make sure that students learn a certain amount of topics, it is quite that simple.  If students from my geometry class are going into an algebra II class with trigonometry the next year where their teacher will expect them to know certain topics, I better do my job and make sure they have learned it.

So how do I, as a PBL teacher, foster the values for the problem-based learning that I have while at the same being true to the curriculum that I know I have a responsibility to?  This is probably one of the biggest dilemmas I face on a daily basis.  Where’s the balance between the time that I can spend allowing the students to struggle, explore, enjoy, move through difficulty, etc. – all that stuff that I know is good for them – while at the same being sure that that darn “coverage” is also happening?

So here’s a little story – I have a colleague sitting in on my classes just to see how I teach – because he is interested in creating an atmosphere like I have in my classes in his.  We have just introduced and worked on problems relating to the tangent function in right triangle trigonometry in the past week and now it was time to introduce inverse tangent.  I do this with a problem from our curriculum that hopefully allows students to realize that the tangent function only is useful when you know the angle.FullSizeRender (3)

So as students realize they can’t get the angle from their calculator nor can they get it exactly from the measurement on their protractor (students had values ranging from 35 to 38 degrees when we compared), one of the students in my class says, “Ms. Schettino, wouldn’t it be great if there was a way to undo the tangent?” and the other kids are kind of interested in what she said. She continues, “Yeah, like if the calculator could just give us the angle if we put in the slope.  That’s what we want.”  I stood there in amazement because that was exactly what I wanted someone to crave or see the need for.  It was one of those “holy crap, this is working” moments where you can see that the kids are taking over the learning.  I turned to the kids and just said, “yeah, that would be awesome, wouldn’t it?  Why don’t you keep working on the next problem?” and that had them try to figure out what the inverse tangent button did on their calculator.  They ended up pressing this magical button and taking inverse tangent of 0.75 (without telling them why they were using 0.75 from the previous problem) to see if they could recognize the connection between what they had just done and what they were doing.

At the end of the class, the colleague who was observing came up to me and said, “How did you do that?” and I said, “What do you mean?” and he said, “How did you get the kids to want to learn about inverse tangent? I mean they just fell right into the thing you wanted them to learn about.  That was crazy.”  I really had to think about that.  I didn’t feel like I did anything honestly, the kids did it all.  I mean what made them all of a sudden care about getting the angle?  Why were they invested?   It doesn’t always happen in my classroom that’s for sure.  This is not a perfect science – there’s no recipe for it to work – take a great curriculum, interested kids, an open, respectful learning environment and mix well?

I do think however that a huge part of it is the culture that has been created throughout the year and the investment that they have made in their ownership and authorship in their own learning. We have valued their ideas so much that they have come to realize that it is their ideas and not mine that can end up driving the learning – and yes, I do end up feeling a little guilty because I do have a plan.  I do have something that I want them to learn, but somehow have created enough interest, excitement and curiosity that they feel like they did it.  It is pretty crazy.

Revisiting Journals: Getting Kids to Look Back

I have been using metacognitive journaling in my PBL classroom since 1995.  I first learned about it the Summer Klingenstein Institute when I was a third year teacher and just fell in love with it.  At that time, the colleagues at my school thought I was crazy trying to make kids write in my classes – it was just “something else for them to do” and didn’t really help them learn but I did more reading on it and there was clearly more and  more research as time went on that showed that writing-to-learn programs especially those that prompt for metacognitive skills really do help in learning mathematics (see my metacognitive journaling link under the Research tab for more info and sample journal entries).

Every once in a while a student will write a journal entry that I think is so thoughtful that I will write about it like this one a few years ago that just impressed me with his insight into his learning process of a particular problem. But other times kids write about their understanding of their learning overall like one I’ll write about today and I am also blown away.

Here’s a student I’ll call Meaghan reflecting on a problem that she found challenging for her.  Really, it doesn’t matter which problem it was or what topic it was, just the fact that she had a hard time with it at first, right?  The most important part was that after she wrote about how to do it correctly, she then took the time to write this: (in case you can’t read her handwriting, I will rewrite it below).

FullSizeRender
Part of Meaghan’s Journal Entry

“This problem was a challenge for me.  When I saw the question, it didn’t look that difficult but once I was trying to solve by [sic my] brain wasn’t thinking on the right track, and it was trying to use prior knowledge that was irrelevant in this case.  I wasn’t making connections to the properties of triangles that I had recently learned.”

Why is this realization so important for Meaghan?  Polya’s Fourth Principle of Problem Solving is “Look Back” – why is this fourth principle so important?  In my mind, this is where all the learning happens.  The three other principles are very clear

  1. Understand the problem
  2. Device a plan
  3. Carry out the plan

These three are all very basic – if they work, right?  But most of the time they don’t work for kids.  It’s the fourth step that we know is the most important – it’s where the critical thinking and analysis takes place.  If this part isn’t taken seriously and the right steps within it are not taken nothing happens, no moving forward, no growth.

So what did Meaghan do?  She realized that she had not made a connection between the triangle properties that we had just learned and how it applied to this problem.  She had not use the correct prior knowledge.  She  just created more openings to other knowledge that she knows- and I know what you’re thinking.  Does this mean that next time she will use the correct prior knowledge in another problem?  From my experience with kids, no, it does not.  But honestly, what I have seen is that the more they realize that there are more possibilities and also that the option of just saying “I don’t get it” or “I can’t do this” is unlikely, the more they will keep trying.

So what did Meaghan do? By just being asked to write a reflection about one problem (every two weeks) she has reinforced her own potential in problem solving on HER OWN.  That she may, in the future, weed out the irrelevant prior knowledge and possibly see the connections to the relevant prior knowledge, with more practice.  I think it’s made her feel just a little bit more confident – and they said it was just “something else for them to do.”