Category: In the classroom

Teaching Circle Concepts with PBL

In a traditional Geometry text, there is a chapter on circles – usually around 8 or 9 – right? Where they introduce a definition, the equation in a big blue box and students learn how to write equations, find the area, circumference and do some interesting problems negative space if they are lucky.  The question then is how are circles connected to the rest of the geometry curriculum?  There is so much more that students could be able to see that goes unseen when circles are compartmentalized like this.  Circles are often introduced in middle school mathematics classes and by the time they get to high school geometry students have seen area and circumference and perhaps even understand a little bit of the irrationality of pi.  What then can a PBL curriculum do to help students understand circle concepts more deeply and in a more connected way?

One of the first types of problems that students are asked to do in the curriculum that I have adapted goes like this:

Find two lattice points that are 5 units away from each other that are not horizontal nor vertical.

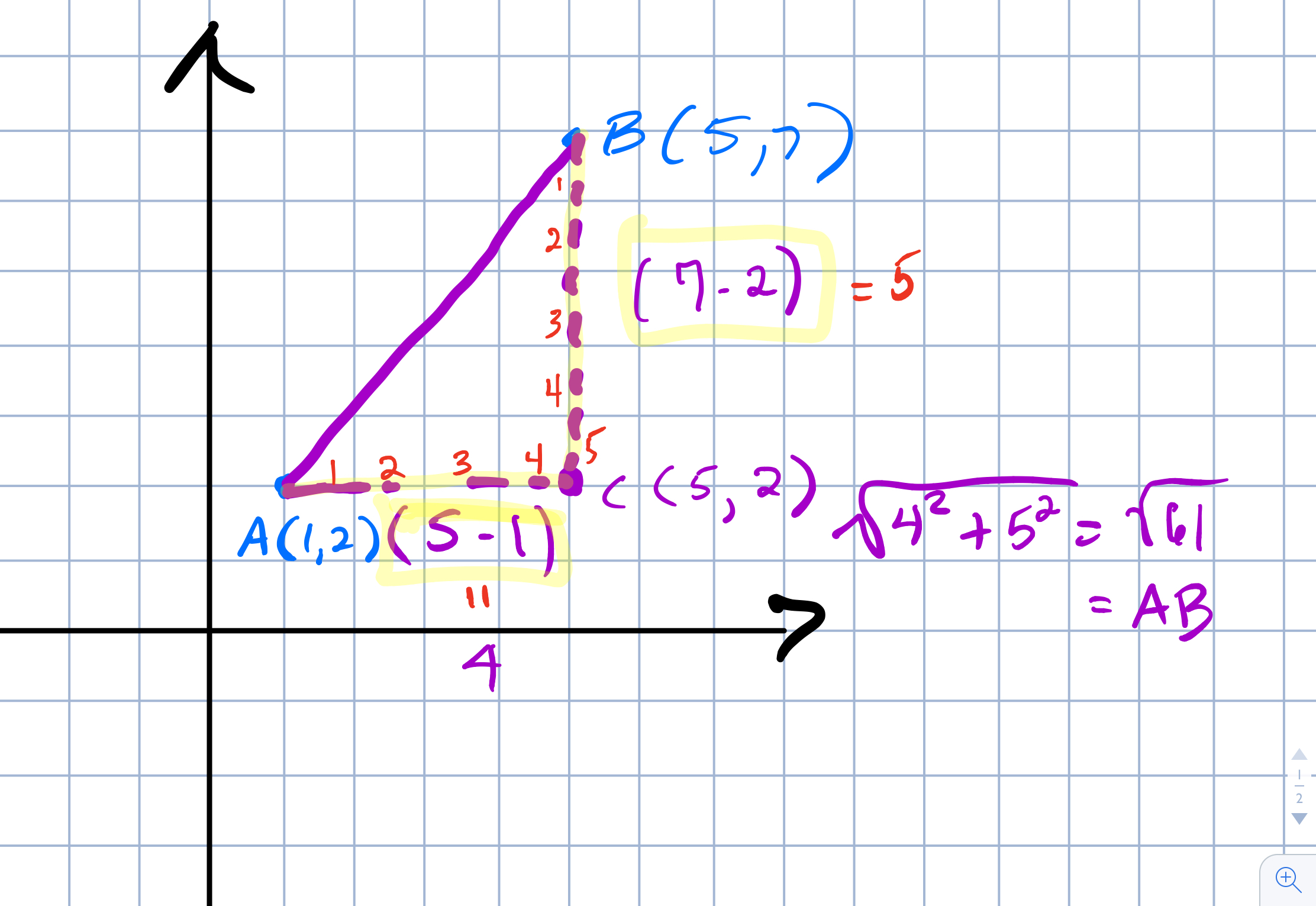
This question is clearly asking for two integer-values points on the coordinate plane that are 5 units from each other but students can’t just count them since the distance is diagonal.  This is often a difficult idea for students at first who are not comfortable with the idea of Pythagorean distance (see previous post about Pythagorean distance).  However, since the beginning of the Math 2 book has so much work with the Pythagorean Theorem, it may be that students are thinking of the distance as the hypotenuse of a right triangle and can think of the 3-4-5 that has shown up in many other problems.  It does take some time for students to be able to think of two points like (1,2) and (4,6) as 5 units away from each other.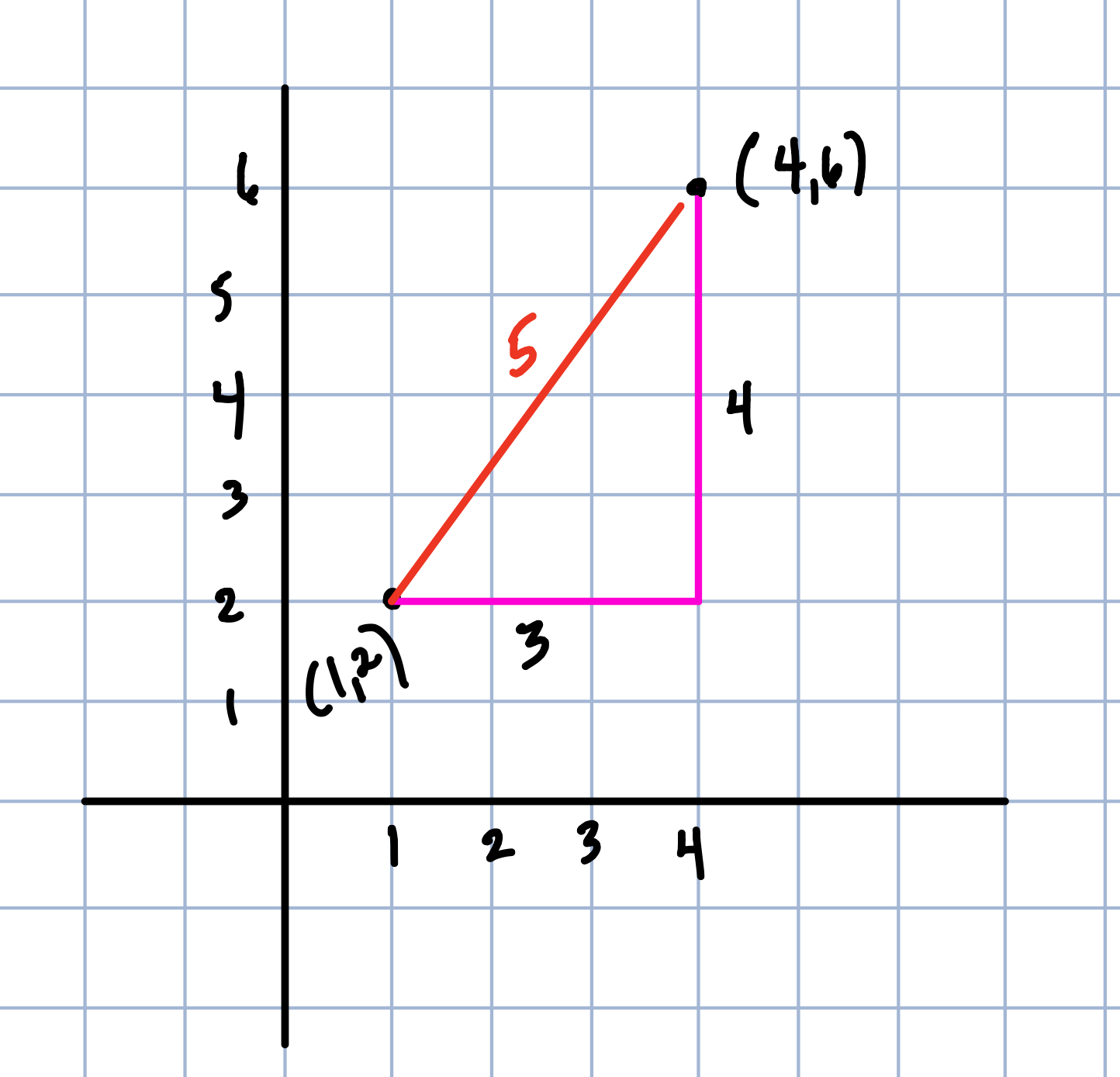

Students are asked other questions about the configuration of points that meet certain criteria and how it would be represented algebraically.  For example:

Describe the set of points that are all 3 units away from the x-axis.  How would you describe this configuration in an equation?

This is trying to get students used to visualizing ALL points that satisyfing a given distance condition and when other conic sections are discussed in later courses, they are prepared to be thinking of configurations as a set of points.  So finally when they are asked to

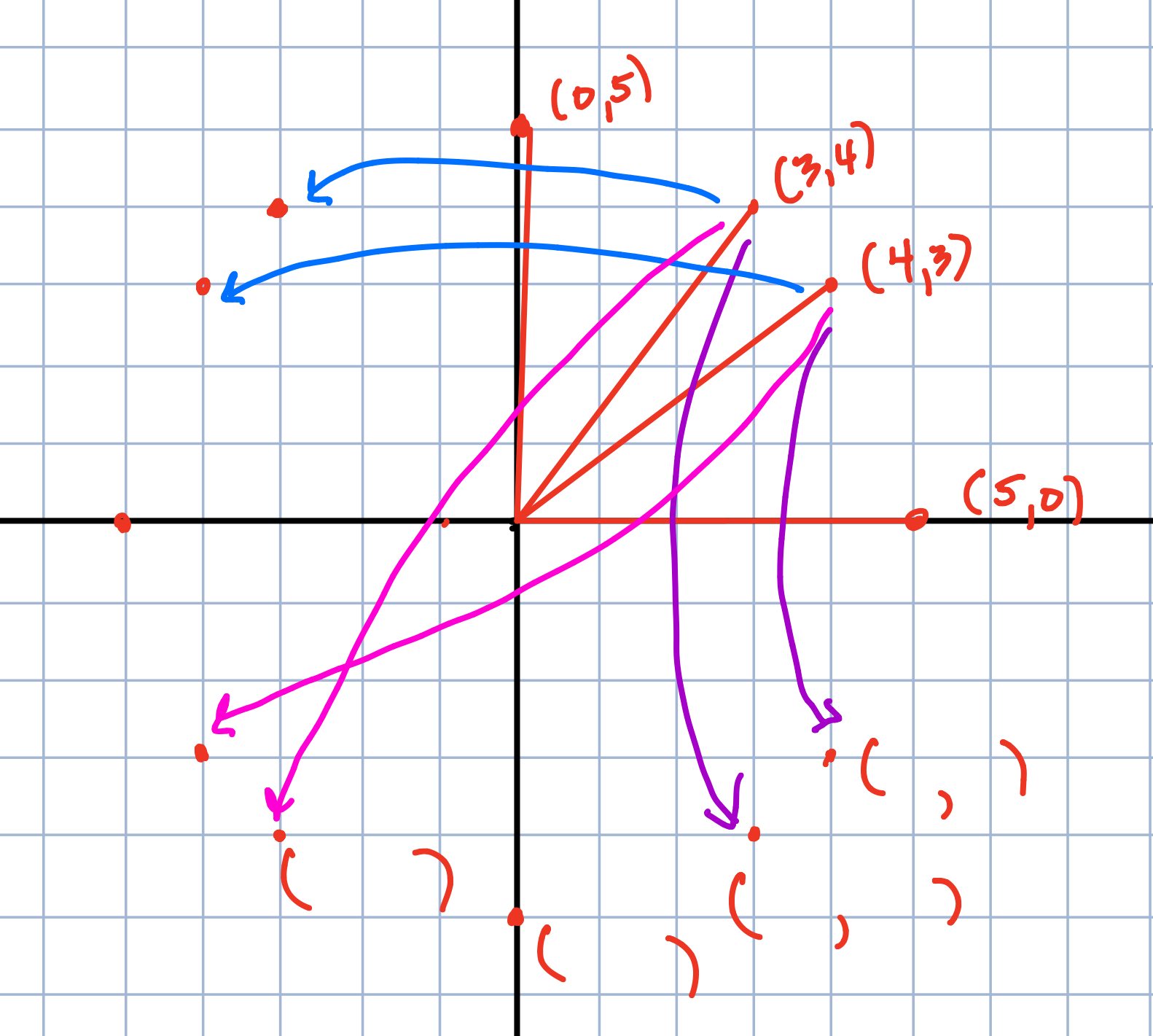
Write an equation using the distance formula that says that P=(x,y) is 5 units from (0,0).  Plot several such points.  What is the configuration of all such points called? How many are lattice points?  [See here for a wonderful journal entry by a student on this question].

This question is the first time that circles are actually introduced and the word “circle” isn’t even in the problem.  The discussion that occurs can be very deep and interesting (as is what happened when the student who wrote that journal entry presented this problem) or it could be very straightforward and benign.  I have been impressed over the year with how well some students understand that a circle must contain points that are all the same distance from the point that is the center.  It is introduced with the distance formula because so much of their work to the point has been based on the distance formula.

Students have a great time discussing the number of lattice points that lie on the circle and where they are.  If they can harken back to the earlier problem about points that are 5 units apart, they recall the 3-4-5 right triangle easily and get the lattice points in the first quadrant.

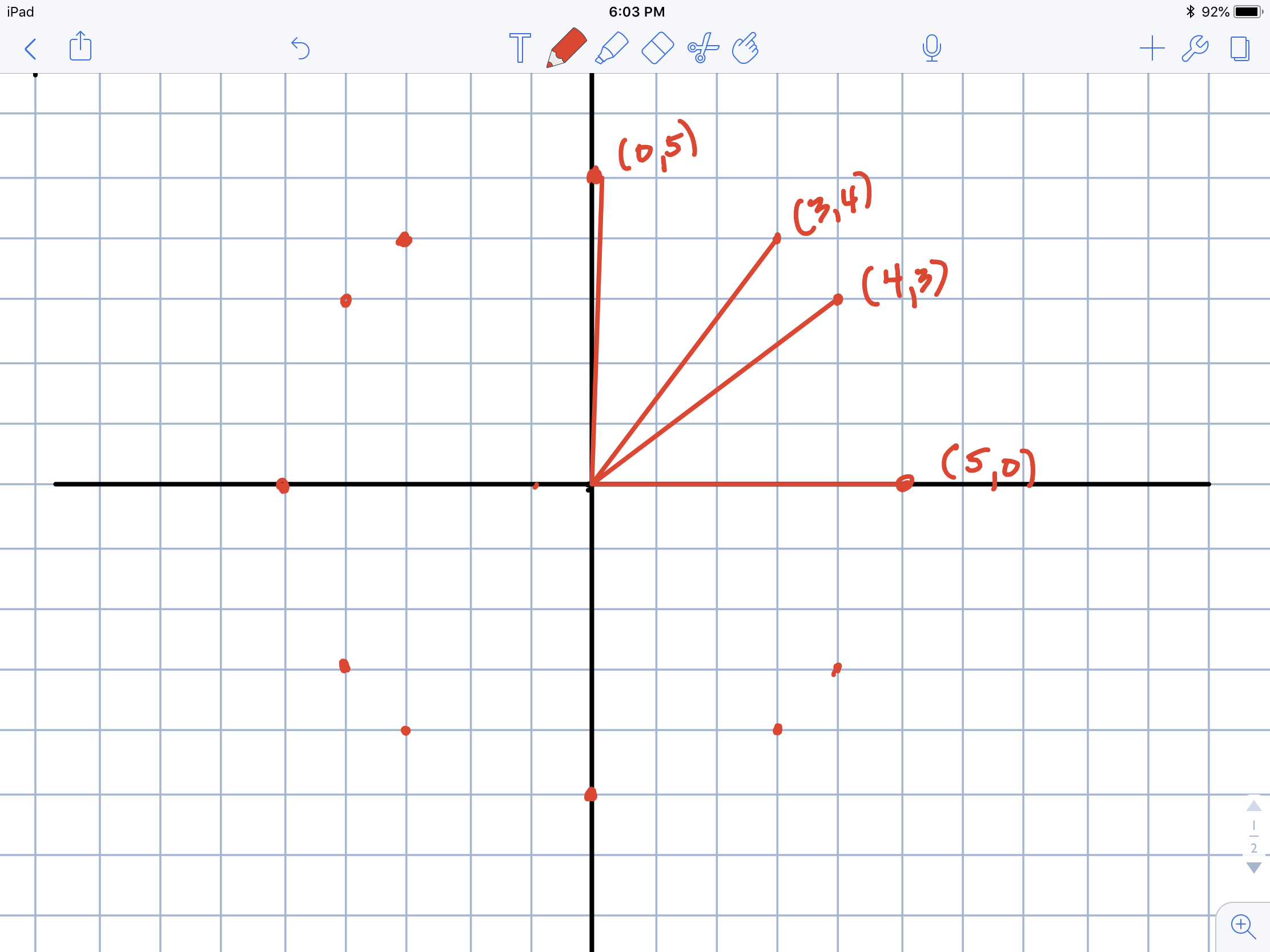
Most students can then use their knowledge of transformations and the symmetry that the circle has and find the coordinates of the of the other lattice points.  This is also a wonderful conversation about reflection over the axes or origin.

 

If the student presenting this problem leaves the equation in the distance formula form without simplifying, that’s even better and sets up the next question:

Explain how you could use the Pythagorean Theorem to obtain the same result.

At this point, it is important to connect the distance of five units, the center of the origin and the idea of the radius being a hypotenuse of a right triange with the coordinates the students just found.  This will be so important later on when students work with the unit circle in trigonometry for thefirst time.

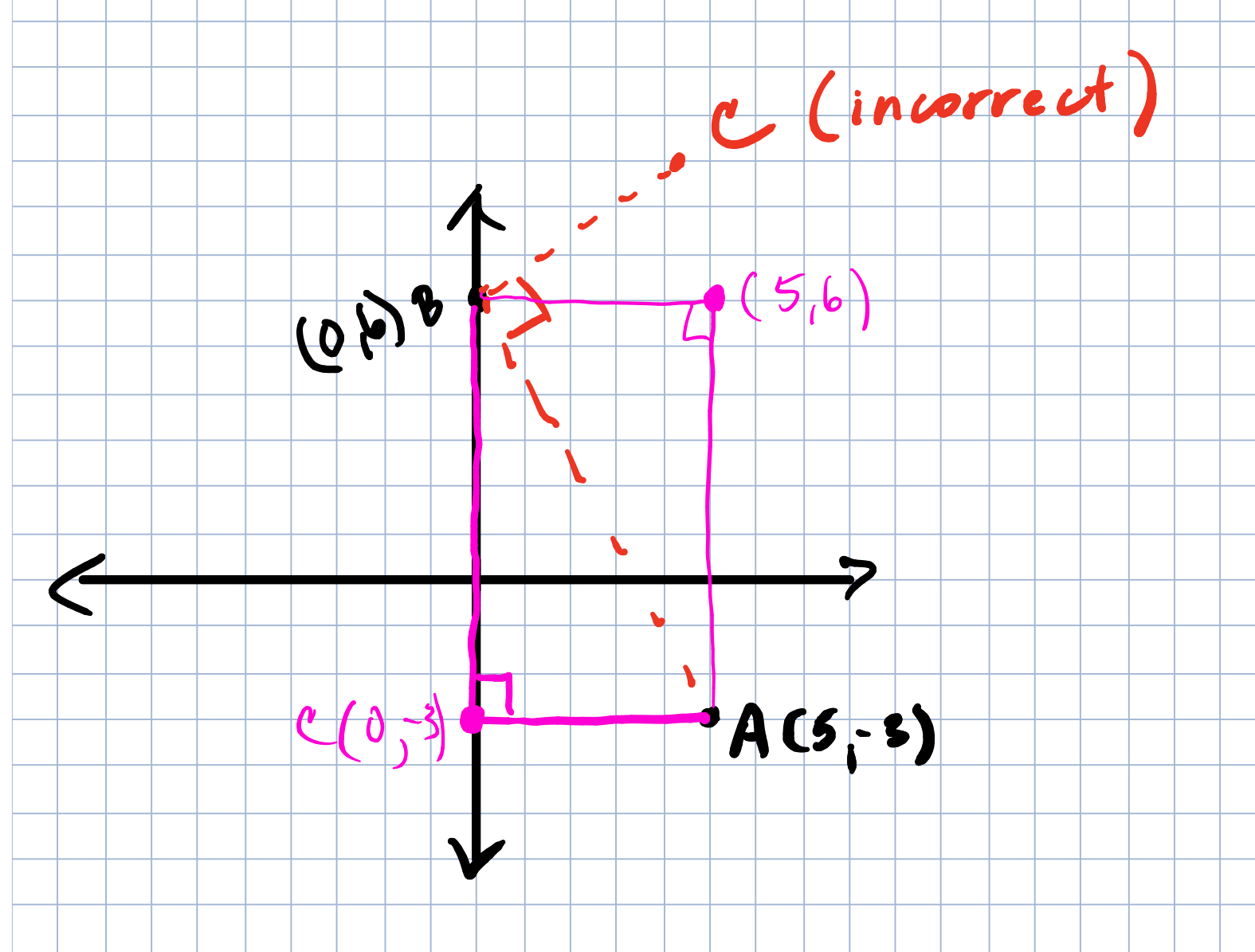
Ask students to start by drawing right triangles where they think they might be in the circle.  Interestingly (and maybe obviously) many of them try to draw it like this (see below) where the right angle is at the origin.  This is a great time for a conversation about where the points are that are “5 units away from the origin,” where that distance is, and which point are they saying is on the circle with the right triangle.  If some student can connect the idea that the radius is supposed to be the hypotenuse and let another student co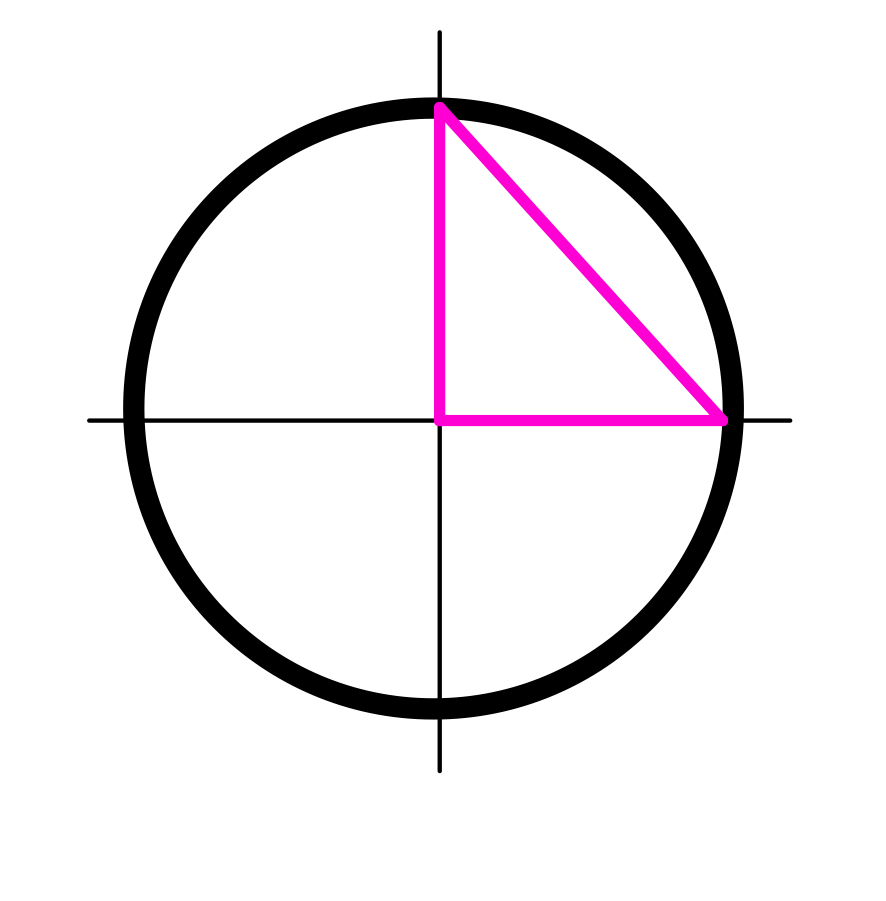me up to the board and make an attempt at the drawing, it is much better than the teacher drawing it for them.  As the discussion moves forward and a student can draw the correct right triangle, I have always tried to get other students to draw other triangles.  The first that usually happens is that students generally draw the right triangles that have the lattice points as the point on the circle.  It takes some time for students to think about the idea that (x, y) can be any point such that x²+y²=25.  This takes some time and discussion.

With a group that is ready, I have also asked students to find the y-coordinates that corresponds to the point on the circle that has the x coordinate that is equal to 1 or 2 and see what they come up with.  This is a great time to see if they truly understand what the equation is telling them.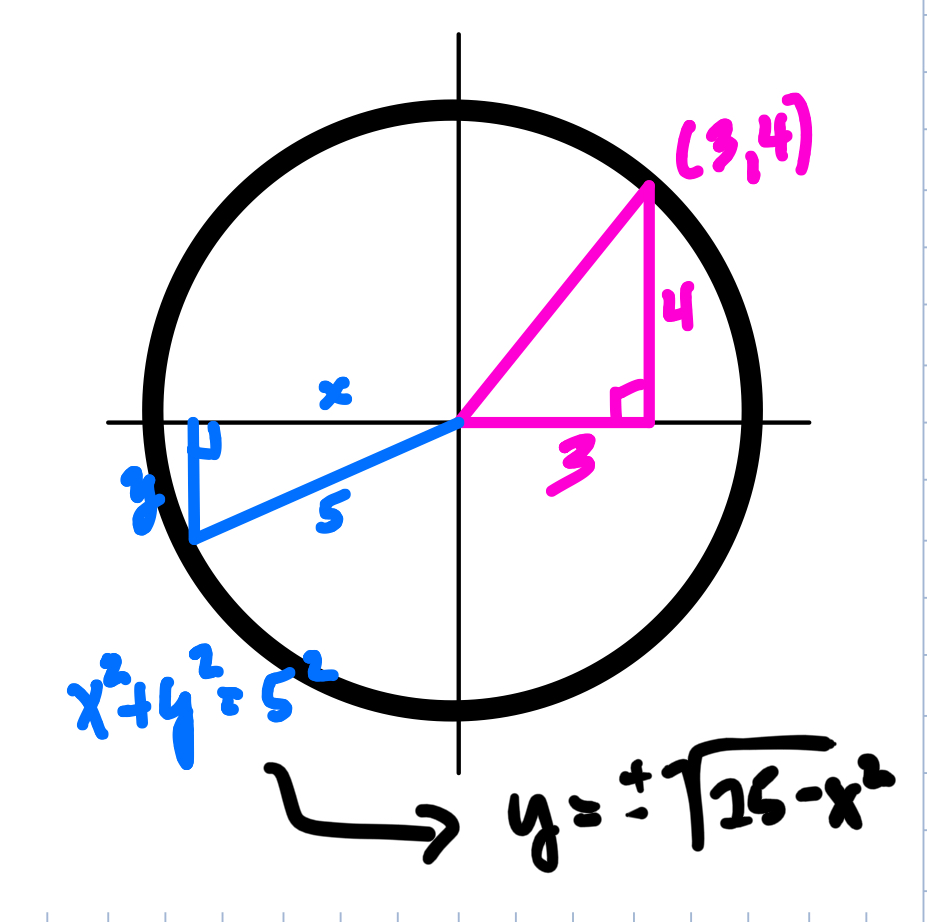

There are many more problems that come after this – some ask for what circles have in common from their equations, some ask for lengths of chords, some are area and circumference problems.  I will write another post on how inscribed angles and arcs are introduced but the idea that circles are all connected to the distance formula and the Pythagorean Theorem is a deep one that runs through the whole curriculum and is important for students to see the connections between the right triangles and the circle itself.

Teaching the “Distance Formula” with PBL

As I write curriculum, I am constantly scouring the Internet for ideas and ways to improve my own work, as we all do.  I was just on the NCTM resources page the other day at their “Reasoning and Sense Making Task Library” and found this description of a task called “As the Crow Flies”:

“The distance formula is often presented as a “rule” for students to memorize. This task is designed to help students develop an understanding of the meaning of the formula.”

OK, wait – shouldn’t this just say, we shouldn’t be presenting the distance formula as a rule for students to memorize?  Instead we should be teaching it for understanding from the conceptual level and allowing students to realize the connection between the Pythagorean idea of distance and how it allows a student to find the distance between two points?  Why should we have a specific task designed to create the understanding after learning the formula when the formula is actually secondary?

There is a series of questions in the problems I have written/edited that allow students to come to this realization on their own.

First, a few basic Pythagorean Theorem problems to practice the format, remind themselves of simplifying radicals, Pythagorean Triples, etc.  Second, some coordinate plane review such as:

  1. Given A=(5,-3) and B=(0.6). Find the coordinates of a point C that makes angle ACB a right angle.

This is really an interesting discussion question for many reasons.  First many students have trouble understanding where the right angle is supposed to be. If they incorrectly read that the angle that should be right is ABC, then they are picturing a different right angle (and also doing a harder problem that we’ll get to soon!) but if they are reading ACB, it’s still an interesting question because there is more than one answer.

Students can sometimes visualize where the right angle can be (even both of the points) but may not be able to get the coordinates.  This discussion is important however because in order to come up with the distance formula later in general (with the x’s, y’s and subscripts – whoa, way confusing!) they need to realize what’s so special about that vertex’s coordinates. So if there is a student who is confused I usually ask the student presenting this problem, “Can you describe the way you found the coordinates for C?” Their answer usually goes something like this: “You just take the x of the one it’s below and y of the one it’s next to.” and other kids are either totally on board, or totally confused.  So then they need to make it a little more mathemtical so every else is on board.  Other kids often chime in with words like horizontal and vertical, x-coordinate and y-coordinate.  This is a really fun, useful and fruitful mathematical discussion in my experience.

We can then move to a problem like this:

2. Find the length of the hypotenuse of a right triangle ABC, where A = (1,2) and B = (5, 7). Give your answer is simplest radical form.

This is generally a problem that is given to students individually to grapple with for homework or in class in groups at the board.  After doing the one discussed above, they at least are prepared to find the vertex of the right triangle and see where it should be.

It’s honestly rare that a student can’t even draw the diagram – especially if they can make the connection with the previous problem. (Connection is one of the four pillars of the PBL Classroom).  One of the things that is often difficult for students is the idea of subtraction of the coordinates.  The can easily count the units to get the sizes of the legs in order to do the Pythagorean Theorem, but in order to generalize, for a later purpose…sorry, don’t want to steal the thunder…subtraction would be an interesting alternate solution method if someone comes up with it – and they usually do.

At this point if someone does come up with it, I usually do ask why can you subtract the coordinates like that to get the lengths of the sides and (you guessed it) there was an earlier problem that had student finding distance on a number line, so, many kids make that connection.

So finally we get to this, maybe a couple of problems later:

Again, students are asked to use their prior knowledge and contemplate a way that they might be able to describe of finding a way to express the distance between two points in a plane.  This is after discussing notation, discussing how to visualize that distance, discussing subscripts, and discussing the purposes (in other problems) of why we might actually need to find the distances between two points. Because the Pythagorean Theorem squares the lengths of the sides (BC and AC) I’ve never had a kid get all upset about the fact that we don’t put the absolute value signs around the difference for the sides – we’re gonna square it anyway, so who cares if it’s negative?  Kids usually say, “if it’s negative, let’s just subtract the other way and it’s be positive.” We just get right to the point that all we are finding is the hypotenuse of a right triangle which has been the Pythagorean Theorem all along.

I generally have students write a journal entry about this amazing revelation for them at the beginning of the year and voila!  It’s right there for them, in their journal for the whole year – no memorization needed.  They understand the concept, know how to use it and actually love the idea because now they can just see a right triangle every time they need a distance.  It’s how so many of my students say that have “never learned the distance formla” – they just use the Pythagorean theorem to find distance.  I love it.

Resources for my NCTM Conference Talk Washington 2018

I hope there’s lots of interest in the lessons that I’ve learned from my years of having students journal. Here are some resources that you could use if you are interested in trying journals in your math classes.

Handout for NCTM Session Handout Schettino NCTM 2018

Blogposts about Journaling:

journals-paper-vs-digital-the-pros-and-cons/

what-i-get-out-of-student-writing/

revisiting-journals-getting-kids-to-look-back/

does-journaling-in-pbl-promote-resilience/

using-journal-writing-in-pbl/

Page: metacognitive-journaling/

Slides for Talk: Slides from Journal Presentation

PBL: High Expectations or Learning to be Self-Directed?

One issue that seems to arise after teachers have been teaching with PBL for some time is the question of how students can remain active learners while listening, taking notes, comparing solutions, being engaged in discussion, etc.  All student-centered mathematics classrooms now have this issue don’t they?  Can a student learn well when they are being active in their learning? How do you allow them to both have agency by being part of the construction of knowledge but also have ownership by taking responsibility for the active part of learning.

Here’s a scenario: Grade 8 class has a student at the board presenting a method of factoring that is obviously confusing everyone – you know, they learned “the box method” somewhere else and are presenting it like it’s just a given that you are supposed to know this.  I’m observing this and I’m seeing at least 5-7 looks of confusion, maybe 1-2 students who are following the student and at least 3-4 who have checked out totally – maybe drawing a tree in their notebook.

How do you maximize this moment?  It is imperative that the teacher move in and ask questions that get at the student presenter’s understanding, especially if the other students are not asking questions.  There may be an air of “oh god, I’m supposed to understand what this kid is talking about” and others will not be asking good questions.

The teacher can ask questions like:

“OK, good work that you have a method that works for you.  Can you back up and explain how this method is showing what the factors of the quadratic are?”

“Let’s slow down a minute and see if there are any questions.”

“Why don’t you explain why you chose the number and variable you did for each box and what those boxes represent?”

“Can everyone else write down a question for …. and then we’ll share out.” (this can include making up a problem for those who do understand and seeing the presenter do another example)

These will bring the moment back to the group, wake them up to the fact that it’s OK to have questions and maybe an alternate method as well.  The kids who have checked out might feel validated in checking out.  But at the same time, checking out shouldn’t be an option. . How can we teach students to remain connected even when they really feel like all is lost?  In PBL, it is most important for student to have the tools in order to do this.

Today I saw this infographic tweeted by Brian Aspinall (@mraspinall) that does an excellent job of summing up ways to have students remain engaged when they want to check out.

Screen Shot 2018-02-23 at 2.59.57 PM

So many of these relate to the expectations for students in the PBL classroom.  Some of my favorites are

1. Reflect in writing – hugely important for the introverts in the PBL classroom and to share the floor and authority.

2. Relate it – not only to “something” you’ve experienced but another problem that you might have done that is connected to it!

3. Control your environment – How engaged you are is really your decision – How can students minimize their own distractions?  Of course day-to-day this will vary, and is developmentally different from grade 8-12 of course, but students, when aware of being distracted, can often find ways to get back into the work.

4. Self-Assess – this is one of my favorites – it keeps them engaged, makes them think critically and thinking ahead.

Allowing kids to know that doing all of these different behaviors in the math classroom is not only OK, but expected and encouraged, is part of teaching with PBL and encouraging the “active” in active learning.

The “Wounded Healer” Archetype in the PBL Teacher

4 Comments

I have been doing a lot more work with teachers this year as I am not in the classroom.  I love watching people teach and talking to them about their teaching.  It is clearly a passion for so many people and the modeling of lifelong learning has been so inspirational for me and their students.

One issue that seems to arise in all PBL classrooms, no matter how progressive the teacher, is this feeling that they need to somehow, someday really just not allow the students to be frustrated.  Even those who buy into the whole PBL, student-centered, productive struggle pedagogy – deep inside they understand the belief from their own education, that math is black-and-white there needs to be some resolution that is acknolwedged and /or provided by the teacher.

I was talking to a friend about this dilemma a while ago (thanks @phiggiston!) and saying how interesting it is to me that a teacher’s belief from their past can, in the moment, while teaching, often override their beliefs in the current pedagogy.  In other words, if a teacher has not experienced independent learning as needed in PBL, it is extremely difficult to not give into the impulse to “save” the students from that feeling of struggle or unease.

Well, coincidentally, @phiggiston has a background in both religious work and in psychotherapy training, so the first the he says to me is, “it’s kind of like the patient-therapist relationship in a way.” And I’m thinking, my teaching is nothing like being a therapist, but of course, I listened intently.  I guess there is a Jungian theory that says that “sometimes a disease is the best training for a physician.”  In fact, Jung goes as far as to say that

“a good half of every treatment that probes at all deeply consists in the doctor examining himself, for only what he can put right in himself can he hope to put right in the patient.”

_____________________________________________________________________________

So what does this mean for PBL teaching?  I had to think of this for a while and also read some Jung as I am not up on the psychological theories that connect to education.  I wasn’t quite sure that this “Wounded Healter” achetype paralleled the PBL teacher as much as I originally thought.  Here are some points:

  • Jung says that for the wounded healer the therapeutic encounter should be regarded as a dialectical process  It’s not just I’m going to the doctor and she’s going to tell me what wrong with me.  There needs to be some kind of dialogue in order for a real healing to happen.  In the classroom, I would argue that this is true about the teacher-student relationship.  Traditionally, it has been that not having dialogue would result in learning that was not as long-lasting, effective and/or connected to the students own ideas.  It is pretty clear that the PBL teacher needs to create the dilectical process in order for the best learning to happen.
  • Jung argues that the physician must help create a safe space where the “patient’s “inner healer” is made available to her unconsciously.” At the same time the physician, should let go of the way she is activiated by the same wounds. This idea is extremely relevant in the PBL classroom.  Why do we want to make students comfortable and relieve their anxiety about mathematical learning?  My take would be because we hate the way it makes us feel. Knowing that struggle is all to close in our memory can actually help us hand over the power to “heal themselves.”  If we can get over that feeling, it will become more of the norm in the classroom.
  • There are risks to this type of teaching – the risk of being vulnerable because you are looking at your own wounds, and also looking fragile to the patient (or student).  This is a very common concern of teachers who are beginning PBL teaching.

“The experience of being wounded does not make him/her less capable of taking care of the patient’s disease; on the contrary, it makes him/her a companion to the patient, no longer acting as his/her superior.”

In other words, it is worth the experience of creating that open relationship.  I go back to Hawkins’ theory of learning (I-thou-It) in which the relationships that exist form a triangle between teacher-student-material.

Hawkins (1974)
Hawkins (1974)

All of these relationships must be nurtured in order for the best learning environment to exist. (For more on this check out Carol Rodgers presentation slides here.)

_____________________________________________________________________________

So does this mean if you did not have this type of experience learning math that you can’t learn to empower your own students in this way?  I think not.  When I ilook back on my own mathematical experiences many of them were extremely traditionally taught.  However, I think what you need to have inside you is both the belief that students are capable of owning and constructing their own knowledge and the ability to create a space that allows them to remain uncomfortable.  You have to be willing to let go of your own insecurities and anxieties about learning math and realize that the more you do that, the more the students will feel it as well.

I am currently working on a quasi-research project about this and when/how PBL teachers choose to intervene in class discussion.  If there is anyone who is interested in helping me out with this, I’d really appreciate it.

Looking at PBL Practice from a Thematic Perspective

2 Comments

So I’m here down in Florida – loving it (all sing-songy like Oprah would say).  I’ve been to so many talks that have been great learning experiences so far.  The weather is beautiful – I went for a very long walk and tried to think about what my talk was missing.  I did a bunch of edits and now I think I’m ready to post it.

Here’s the powerpoint of the talk:

Here’s the document that I handed out with some “threads” of themed topics:

Three Threads Document

Please contact me with any questions, comments or concerns – I love talking to people about PBL and my work.

How do you justify the time that PBL takes?

4 Comments

I just wanted to respond to a really great question that someone asked on Twitter the other day.

This is a common concern of teachers starting out with the idea of PBL. What does “Class Discussion” mean, first of all? I would agree that discussion does “eat up valuable” time in class on a daily basis, for sure. But what is actually happening in that discussion where something else would be normally happening in the math classroom? What does the discussion replace?

In my mind the discussion itself replaces the lecture, teachers ‘doing of problems” for the kids to then repeat, then kids often sitting on their own or in pairs doing problems that were just like the ones the teacher showed them how to do. The importance of the class discussion (which honestly is the main idea of PBL) is for students to share their ideas of prior knowledge, connections between problems, where they are confused and see where others were not confused and what prior knowledge and experience they brought to the problem.

Here’s a diagram that I use when doing PD work with PBL teachers to help explain all of what is supposed to be happening during class (it’s a lot!)


The student presentations are really just a jumping-off point. It is not just for students to explain “how they did a problem” – as they say – or they think what they’re supposed to do. The steps of Hmelo-Silver’s “process of learning in PBL” diagram that I’ve circled in pink is what students would/should do for homework. However, the part that is circled in blue is actually the learning process that happens in the class discussion – so is this time that has been “eaten up” in class or is it actually a very necessary part of the important learning, reflection and self-regulation of the process that needs to happen?

Is this harder for students? Heck, Yeah. There is so much more focus, listening, questioning and reflection that is needed in order for this process to be successful and productive. But there are ways to make it easier for students and that’s what the “class discussion” time is for. It takes a lot of practice and mastery on the teachers’ part to realize what is needed. Making mathematics discussion productive is a very important part of teaching in PBL and definitely not a part that should be seen as subtle, intuitive or straightforward.  There is so much more to this that I can not put in a single blog entry, but it’s definitely worth beginning the discussion.  Would love to hear others’ thoughts.

I’ve looked at life from both sides now…

4 Comments

This past July, I spent a few days at the MAA Mathfest in Chicago for the first time. The main reason I went was because the Academy of Inquiry-Based Learning was having a Conference within the Mathfest with the theme of “Diversity in IBL.”  IBL is generally what college faculty call the type of teaching and learning that many of us at the secondary level has been calling PBL for years.  I was so interested to hear many mathematics professors talking about the struggles of writing curriculum, dealing with facilitating discussion, using writing – all of the same parts of this type of teaching that we may have been talking about for so any years.  I highly suggest that we could benefit from talking to each other.  If you would like to get involved with this movement, Stan Yoshinobu, the Director of the Academy of Inquiry-Based Learning, has put forth some challenges for his community.  Check them out.

One of the most interesting talks that I attended was by a professor from Denison University, Lew Ludwig, titled, “Applying Cognitive Psychology to the Mathematics Classroom.”  As a devout social constructivist, I generally like going to talks where I can learn more about other views of education.  Seeing both sides definitely helps me understand many of the views of my colleagues and see if evidence supports my own perspective. Ludwig had published a review of another article that was titled, “Inexpensive techniques to improve education:  Applying cognitive psychology to enhance educational practice”(Roediger and Pye, 2012).

Basically, the presentation summarized three simple techniques that cognitive psychology had evidence helped student learning. The three techniques were called

  1. The distribution and interleaving of material and practice during learning.
  2. Frequent assessment of learning (test-enhanced learning, continual assessment)
  3. Explanatory questioning (elaborative interrogation and self explanation; having students ask themselves questions and provide answers or to explain to themselves why certain points are true).

In the original article, the authors write:

“Repetition of information improves learning and memory. No
surprise there. However, how information is repeated determines
the amount of improvement. If information is repeated back to back
(massed or blocked presentation), it is often learned quickly but
not very securely (i.e., the knowledge fades fast). If information is
repeated in a distributed fashion or spaced over time, it is learned
more slowly but is retained for much longer”

When this was reported, I was first in shock.  I couldn’t believe I was hearing something in a presentation about Cognitive Psychology that was actually supported by the definition of PBL that I use.  The curriculum I use takes the idea of looking at topics and teaching them over a longer time span, but distributed among other topics.  I have called this decompartmentalization of topics, which helps students see the connectedness of mathematics.

The second idea, consistent assessment, is based on the concept that testing is not really a great measure of how much a student has learned, but it actually solidifies the learning that has occurred.  So three groups of students were given different ways of learning by reading a passage of information. The first group read a passage four times. The second group read the passage three times and had test.  The third group read the passage once and was tested three times.  Their performances on tests on the information in the passage 5 minutes later and then one week later.

Diagram of retention testing research
from Roediger & Pye (2012) p.245

So if we connect the idea that testing is not the best method of seeing how much students have learned and the fact that consistent assessment actually helps students retain their knowledge, what I do in my PBL classrooms, is not only “test” but do all sort of forms of assessment (writing, oral assessment, hand-in homework with feedback, labs, quizzes, problem sets, self-assessment, etc.) alternately throughout the term.  There is probably not a week where students are not assessed in at least 2 ways. I feel that this has led students to have good retention of material and the assessments are strong measurements of their learning.

The last one was the one I was most excited to hear about – explanatory questioning.  This seemed to give students so much more responsibility for their own learning than traditional cognitive psychology as I had understood it.  The authors of this study claim that explanatory questioning can be broken in to two areas:

Elaborative Interrogation – students generating plausible explanations to statements while they are studying and learning.  This speaks directly to the idea of mathematical discussion and how students generate explanations when they ask themselves “why?”

Self-Explanation – students monitoring their learning and describing, either aloud or silently some features of their learning.  This idea can be found all over the PBL classroom but in mine, it’s generally found most in metacognitive journaling where students use self-explanation the most.

“Obviously, the elaborative interrogation and self explanation are related because both strategies encourage or even require students to be active learners, explaining the information to themselves (perhaps rephrasing in language they understand better) or asking themselves why the information is true.”

I honestly couldn’t believe what I was reading – this is an article on educational methods based on cognitive psychology that is suggesting that we require students to be active learners and “explain the infomation to themselves”?  This is lunacy.  I have been teaching for 25 years where students have been complaining to their parents that they have had to explain things to themselves – who would’ve known that I was applying cognitive psychology?

My guess is that these ideas are only enhanced by the social aspect of the classroom and other constructivist ideas – clearly the constructivitst classroom in enhanced by or agrees with some of these cognitive psychology methods as well.  Listening to both sides of the theories is actually helpful and I’m seriously going to continue doing this! Although I never thought that there might be strong connections between cognitive psychology theories and PBL, I do know that it’s life’s illusions I recall and I “really don’t know life, at all.”

PBL and second language learners

2 Comments

As I am not going to be in the classroom next year, I have been going through some old boxes from my study and as many people who have been teaching for a long time have, I have boxes and bags full of cards from past students.  I spent the afternoon one day going through these, reminiscing about so many great kids that I remember.  One of them I had a card from the beginning of her freshman year and also one from the end of her senior year.  Crazy!!

I don’t claim to be an expert in emergent English language learners and mathematics at all.  I did have 10 years of teaching experience at a school (Emma Willard) where they had an ESL program and many students came into my mathematics classes who were not proficient in the English language.  I do think those girls knew what they were getting themselves into and were up to the challenge, but some of them were very frightened.

Since she has now been out of college for a while, I would assume it’s ok for me to share this on my blog.  Here is the card she gave me as a new student in 2001:

Jinsup's card from freshman year
Jinsup’s card from freshman year

This card was written with the voice of a student who was used to a very structured, repetitive mathematics class and I believe she knew that coming into the U.S. things would be different, but possibly not as different as they were in my class.  When she said, “I’m so nervous that you will let me to talk a lot in the class” I’m sure she was saying that she was nervous that I would expect her to contribute to the class discussion.  What I did with many of those students, including Jinsup, was I focused in the beginning on letting them listen and write.  I gave them lots of feedback on their journals and made sure they had the correct vocabulary and that their grammar in their writing made sense.  I allowed them to ask more questions initially than to present their ideas until their confidence became stronger.  Jinsup, as most Korean and Japanese students did, had excellent skills, as that was what their math education had focused on since elementary school.  However, she was not very good at reasoning, sense-making or critical thinking on her own.  It was almost as if she had not been asked to communicate about mathematics, as she was trying to say in her note to me.

However, she ended up doing very well in that first class and then I taught her again in precalculus (which we called Advanced Math) and then in BC Calculus her senior year.  Her excellent background allowed her to focus on the reasoning aspects of all of these courses and in the end, I was very impressed with her growth.  She really got the best of both worlds – the skills from her Asian mathematics education and the collaboration, communication and reasoning skills from the PBL here.

This is the note she wrote me at the end of her senior year:

Jinsup's card at end of her senior year
Jinsup’s card at end of her senior year

Although I know this is only an anecdote and I don’t really have research evidence that PBL totally works with ELLs I do have confidence that with the right environment and patience, it is actually a great way of teaching for many of these second language learners.  It allows them to find their voice in a language that is already new to them but at the same time have some practice in terminology that they may have heard before.  I think this might be my next interesting research project – if anyone has some thoughts on this I’d love to hear them.

What I get out of Student Writing

I have been using journaling in math class since 1996 – which was a really important year in my teaching career for lots of reasons, but it was definitely because I was introduced to the idea of math journals.  Since then I’ve done many different iterations for what my expectations are.  Even this year I did something new where I allowed students to write about errors they made on assessments in order to attempt to compare their assessment problems to what they did on homework in the hope of reflecting on the work pre-assessment for future problem sets.

However, a lot of students still use their journal almost like a problem-solving conversation with me, especially after we have already gone over a problem and they still don’t understand a method.  Here is one I ran across just the other day in my lower-level geometry class and thought it just perfectly expressed some of the goals I am hoping to accomplish with journaling.

I’ll call this student Cindy and we had just introduced the theorems about parallel lines through a geogebra lab and this had been the first problem they looked at that took the concepts out of the context of the lines and threw it into a triangle.  For many students this might be an easy transfer of skills (including the algebra, other theorems, etc.) but for the kids I have – not necessarily.  Here is what Cindy wrote:file_001-1

The first thing that Cindy does in her journaling is make her own thinking explicit (which I love).  She is stepping me through her thinking and the questions that arose for her.  This is actually a major step for many students who are confused – are they able to even know what they are confused about?

She writes: “I know the problem probably deals with the parallel line theories that we dealt with.” and then lists the types of angles we studied and then with a big “OR” says “maybe it has something to do with the sum of the angles of parallelograms and triangles?”  Little does she know that what she is doing is practicing synthesizing different pieces of prior knowledge – is it overwhelming to her? – possibly, but she went there and that’s so great!  I wanted her to know that I was excited that that she even thought about the sum of the angles so I gave her some feedback about those ideas.

She wrote down what she knew about the sums of the angles which we had also studied.

She writes her first equation to think about: “5x-5/=180” using one of the angles in the top triangle.  I would’ve loved to know where that was coming from.  What made her write that?  She then notes that “but it wouldn’t work because if x is the measure of the angle than the equation should be set to 180”

There is so much that this tells me about her confusion.  She is not understanding what the expression 5x-5 is supposed to be representing in the diagram I think, or she isn’t connecting what x is “not representing” (the angle) and the whole expression is representing too.  She also is confused about between the sum of the whole triangle’s angles and just that one angle.

She then looks at the two expressions she is given, 5x-5 and 4x+10 and I think makes a guess that they are corresponding angles – she doesn’t give any reason why they are corresponding.  She just asks the question.  But the cool thing is she says “Let’s try it.”  I love that.  Why not – I am always encouraging them to go with their ideas and the fact that she tries it is wonderful.  The funny thing is she does end up getting the same value for the two angles so she asks: “Does this mean that this is correct?” and then “What do I do for “6y-4?” and still has not connected many of the ideas line the fact that these angles are a linear pair and that’s where the 180 comes into play, or even why the angles were corresponding in the first place.  So many questions that she still has, although I am encouraged by her thinking and risk-taking.

This journal entry allowed me to have a great follow-up conversation with Cindy and she was able to talk to me about these misconceptions.  I’m not sure I would’ve had this opportunity to clarify these with her if she had not written this journal entry and then she would not have done so well on the problem set the following week.  I just love it!  Let me know if you use journals and if you feel the same clarifying or communicative way about them too.

See my website for lots of sample entries and also other blogposts and resources about journaling if you are interested.