Category: Conferences

A Total Win…with lots of understanding

Before I left for the Anjs S. Greer Math Conference last week, I read an amazing blog entry at the Math Ed Matters website by Dana Ernst and Angie Hodge that was talking about Inquiry-Based Learning and the mantra “Try, Fail, Understand, Win.”  The idea came from one of Prof. Ernst’s student course evaluations this past spring as his student summed up his learning experience in such an IBL course.  This blog post was so meaningful to me because for each of these four words, the authors wrote how we as teachers (and teacher educators) can take this student’s perspective towards our own work.  I decided to attempt to take this attitude going off to my own conference with two courses to give and three smaller talks.  It was sure to be a busy week.

And in fact, it really was.  I had very little time to sit and listen to others’ work, which I really was quite sad about.  However, in my own classes I was so impressed with the amount of enthusiasm and excitement my participants had for PBL and their own learning.  As I sat in front of my computer this morning reading the course evaluations and their tremendously helpful input, it finally occurred to me how truly powerful the experience had been for my participants.  Many of them became independent thinkers and knowers about PBL and feel so much more knowledgeable and prepared for the fall.    Part of the class time is spent in “mock PBL class” where I am the teacher/facilitator and they are the students doing problem presentations.  We then sit and talk about specific pedagogical questions and distinctions in classroom practice.  Some of the class time is spent in challenging problem solving which is where I also learn so much from the participant’s different perspectives. “We win when we realize there’s always something we can do better in the classroom” – as Ernst and Hodge write.

The now Infamous ‘French Garden’ Problem

I want to give a huge shout out to all of my participants from last week and encourage them to keep in touch with me.  Many of you wrote in your evaluations that you still have many questions about your practice and how to integrate your vision of PBL in your classroom.  I will always be only an email away and hope that you continue to question your practice throughout the year.

My plan is to try to write some blog posts at the end of the summer/beginning of the year in order to respond to some of the remaining questioning while you plan for the beginning of the school year such as:

  1. How to plan for week one – writing up a syllabus, creating acceptable rules
  2. Helping students who are new to PBL transition to it
  3. Assessment options – when to do what?
  4. Working hard to engage students who might not have the natural curiosity we assume

If you can think of anything else that you might find helpful, please post a comment or send me a message and I’d be happy to write about it too!  Thanks again for all of your feedback from the week and I look forward to further intellectual conversation about teaching and PBL.

Anja S. Greer Conference 2013

What a great time we had this week in my courses!  I am so excited by all of the folks that I met and the CwiC sessions of other leaders that I went to.  Pretty awesome stuff presented by Maria Hernandez from NCSSM, my great colleague Nils Ahbel, Tom Reardon, Ian Winokur, Dan Teague, Ken Collins and many others.  I was so busy that I didn’t get to see many other people’s sessions so I feel somewhat “out of it” unfortunately.

I want to thank everyone that came to my CwiC’s and remind them to be sure to go and pick up my materials on the server before they leave.

For my participants – here are the links to the course evaluations:

Moving Forward with PBL: Course Evaluation

Scaffolding and Developing a PBL Course:  Course Evaluation

Linking Theory to Practice: A Shout-Out to ‘savedabol’

This past January, I gave a key-note address at the ISOMA conference in Toronto and posted my slides from that talk on my academia.edu site that I thought would be a good place for me to easily give other people access to my work. (along with my website).  Academia.edu is great because it gives you lots of information about the stats of surfers who come and look at your information.  All of a sudden I saw that this powerpoint had more than something like 400 views and I couldn’t believe it.  I had to see who was searching and looking at this slideshow.

I quickly realized that someone had seen it, liked it and posted something about it on reddit.  There were only a few comments but one of them went something like this:

“I think the single worst part of being a teacher is sitting through PowerPoints like this, while some earnest non-classroom pedagogue tells us the bleeding obvious.”

Whooo – that one stung…my first instinct was to try and find out who that person was and defend myself to the ends of the earth.  Anyone who calls me a non-classroom pedagogue deserves to be righted…but then I kept reading…and someone with the alias ‘savedabol’ wrote this:

‘Carmel Schettino (the author) led a seminar I took at the Exeter math conference last summer. She is incredible. I can assure you that she is not a non-classroom pedagogue. She has been in the classroom nonstop for at least 20 years (that I know of). She is particularly scholarly when it comes to PBL and other ed topics, but that doesn’t make her irrelevant to what we do every day. Near the end she gives some great resources.’

I can’t tell you how affirmed I felt by ‘savedabol’ and I want to just let them know how nice that was of them to share their thoughts about my work with them.  I have been in the classroom non-stop since 1990 (except for two terms of maternity leave and one term of a sabbatical when I was a full-time student myself) and I pride myself in researching as much as possible about what I do.

I do wish that the first poster had had the chance to hear me speak instead of jumping to the conclusions they had – and it definitely got me thinking about something that was discussed last year at the PME-NA conference in October 2012.  I was one of maybe just a few people in the special category of math teacher/educator/researcher/doctoral students at this research conference where many of the math research folks were talking about ways in which they could breach the great divide of the theory people (them) and the practice people (us).

For many years I have lived this double life of both theory and practice and I have to say, I love it.  Having just finished up my Ph.D. and teaching full time was probably one of the toughest things I’ve had to do in my life, but having my mind constantly in both arenas has only helped me be a better teacher and a better researcher.

Jo Boaler is a great researcher at Stanford University who is doing great work in outreach between theory and practice this summer by offering a free online course called “How to Learn Math.”  It’s a course for k-12 teachers that is grounded in the most recent research in math education.  What a great idea!  She is sharing some of her wisdom freely online with k-12 teachers who want to spend some time learning about new ideas themselves.  I know I’m in.

In August 2008, the NCTM put together a special Research Agenda Project to work on recommendations for just this cause and you can see their report here.  One of the major recommendations that came out of their work was to not only emphasize the need for communication between researchers and practitioners, but in my view to help them realize that this communication would benefit both parties equally.  We all have something to share with each other and I know that I appreciate every classroom practitioners’ experiences.  I learn something from every teacher that ends up in my workshop every summer and often end up using many of their ideas as they do mine.

So let’s keep supporting each other both in real life and virtually, and realize that often times, the “bleeding obvious” is something that needs to be stated and discussed over and over again to be sure that we are still talking about it with the right people.

PBL – Students making Mathematical Connections

As someone who has used Problem-Based Learning for almost 20 years and sad to say has never been part of a full-fledged Project-Based Learning curriculum, what I know best is what I call PBL (Problem-Based Learning).  I know there is a lot of confusion out there is the blogosphere about what is what, and with which acronyms people use for each type of curriculum.  I did see that some people have been trying to use PrBL for one and PBL for the other, but I guess I don’t see how that clarifies – sorry.

So when I use the acronym PBL in my writing I mean Problem-Based Learning and my definition of Problem-Based Learning is very specific because it not only implies a type of curriculum but an intentional relational pedagogy that I believe is needed to support learning:

Problem-Based Learning (Schettino, 2011) – An approach to curriculum and pedagogy where student learning and content material are (co)-constructed by students and teachers through mostly contextually-based problems in a discussion-based classroom where student voice, experience, and prior knowledge are valued in a non-hierarchical environment utilizing a relational pedagogy.

Educational Psychologist and Cognitive Psychologists like Hmelo-Silver at Rutgers University have done a lot of research on how students learn through this type of scaffolded problem-based curriculum dependent on tapping into and accessing prior knowledge in order to move on and construct new knowledge.  There was a great pair of articles back in 2006/2007 where Kirschner, Sweller & Clark spoke out against problem- and inquiry-based methods of instruction and Hmelo, Duncan and Chinn responded in favor.  I highly recommend reading these research reports for anyone who is thinking of using PBL or any type of inquiry-based instruction (in math or any discipline).  It really helps you to understand the pros and cons and parent and administrator concerns.

However, after you are prepared and know the score, teachers always go back to their gut and know what works for their intuitive feeling on student learning as well.  For me, in PBL, I look at how their prior knowledge connects with how, why and what they are currently learning.  One of the best examples of this for me is a sequence of problems in the curriculum that I use which is an adaption from the Phillips Exeter Academy Math 2 materials.  I’ve added a few more scaffolding problems (see revised materials) in there in order to make some of the topics a bit fuller, but they did a wonderful job (which I was lucky enough to help with)and keep adding and editing every year. The sequence starts with a problem that could be any circumcenter problem in any textbook where students use their prior knowledge of how to find a circumcenter using perpendicular bisectors.

“Find the center of the circumscribed circle of the triangle with vertices (3,1), (1,3) and (-1,-3).”

Students can actually use any method they like – they can use the old reliable algebra by finding midpoints, opposite reciprocal slopes and write equations of lines and find the intersection points.  However, I’ve had some students just plot the points on GeoGebra and use the circumcenter tool.  The point of this problem is for them to just review the idea and recall what makes it the circumcenter.  In the discussion of this problem at least one students (usually more than one) notices that the triangle is a right triangle and says something like “oh yeah, when we did this before we said that when it’s an acute triangle the circumcenter is inside and when it’s an obtuse triangle the circumcenter is outside.  But when it’s a right triangle, the circumcenter is on the hypotenuse.”

Of course then the kid of did the problem on geogebra will say something like, “well it’s not just on the hypotenuse it’s at the midpoint.”

 

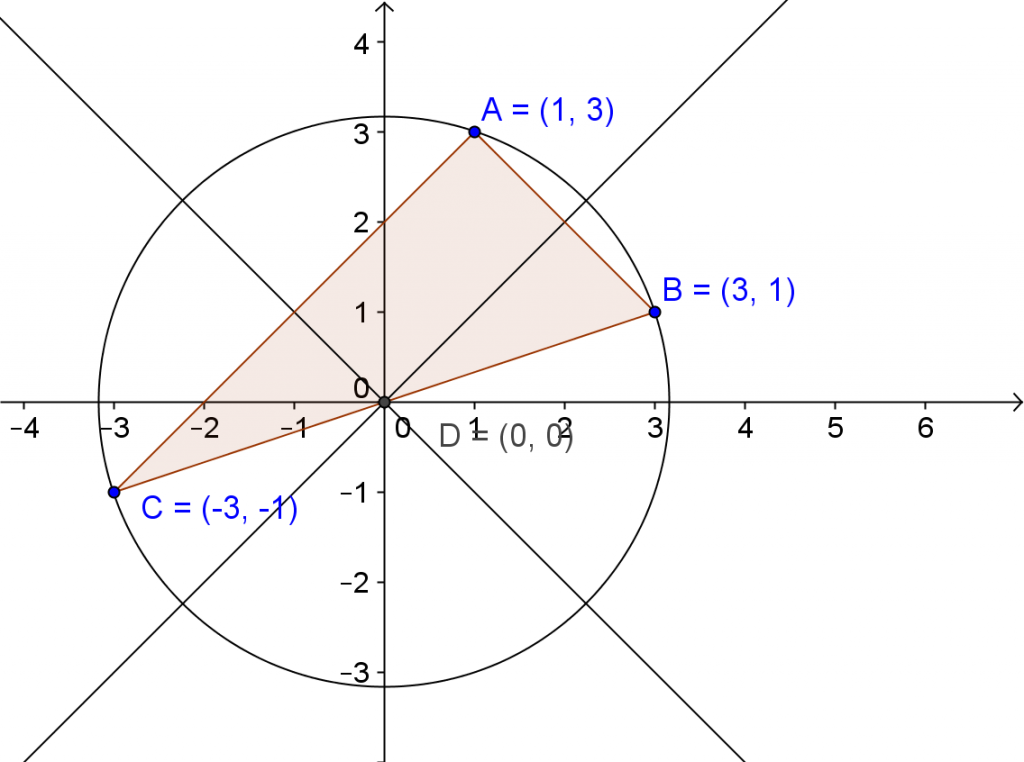
Dicussion will ensue about how we proved that the circumcenter of a right triangle has to be at the midpoint of the hypotenuse.

A day or so later, maybe on the next page there will be a problem that says something like

“Find the radius of the smallest circle that surrounds a 5 by 12 rectangle?”

Here the kids are puzzled because there is no mention of a circumcenter or triangle or coordinates, but many kids start by drawing a picture and thinking out loud about putting a circle around the rectangle and seeing they can find out how small a circle they can make and where the radius would be.  When working together oftentimes a student see a right triangle in the rectangle and makes the connection with the circumcenter.

A further scaffolded problem then follows:

“The line y=x+2 intersects the circle  in two points.  Call the third quadrant point R and the first quadrant point E and find their coordinates.  Let D be the point where the line through R and the center of the circle intersects the circle again.  The chord DR is an example of a diameter.   Show that RED is a right triangle.”

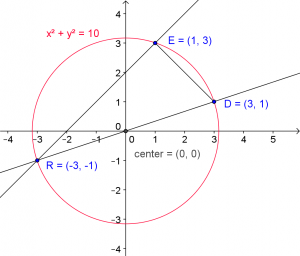
Inevitably students use their prior knowledge of opposite reciprocal slope or the Pythagorean theorem.  However, there may be one or two students who remember the circumcenter concept and say, “Hey the center of the circle is on one of the sides of the triangle.  Doesn’t that mean that it has to be a right triangle?”  and the creates quite a stir (and an awesome “light bulb” affect if I may say so myself).

A few pages later, we discuss what I like to call the “Star Trek Theorem” a.k.a. the Inscribed angle theorem (I have a little extra affection for those kids who know right away why I call it the Star Trek Theorem…)

I will always attempt to revisit the “RED” triangle problem after we discuss this theorem.  If I’m lucky a student will notice and say, “Hey that’s another reason it’s a right triangle – that angle opens up to a 180 degree arc, so it has to be 90.”  and then some kid will say “whoa, there’s so many reasons why that triangle has to be a right triangle”  and I will usually ask something like, “yeah, which one do you like the best?” and we’ll have a great debate about which of the justifications of why a triangle inscribed in a circle with a side that’s a diameter has to be right.  So who are the bigger geeks, their teacher who names a theorem after Star Trek or them?

References:

Kirschner, P. A., Sweller, J., & Clark, R. E. (2006). Why minimal guidance during instruction does not work: An analysis of the failure of constructivist, discovery, problem-based, experiential and inquiry-based teaching. Educational Psychologist, 41(2), 75-86.

 

Hmelo, C. E., Duncan., R.G., & Chinn, C. A. (2007). Scaffolding and achievement in problem-based and inquiry learning: A response to Kirschner, Sweller and Clark (2006). Educational Psychologist, 42(2), 99-107.

 

Defying Gravity as a Means to Learning from Mistakes

There’s a lot of blogging, writing and research (and anecdotal stories) out there these days about trying to foster the value in students for the appreciation in failing.   I even wrote a blog entry two years ago entitled “modeling proper mistake-making” way before I read anything or watched any videos on the Internet.  From teaching with PBL for over 17 years, I am a pro at making mistakes and watching students struggle with the concept of accepting the idea of learning from their mistakes.  This is so much easier said than done, but it is clearly something that grow to love even if only for a short time.

Last April, I had the pleasure of hearing Ed Burger at the NCTM national conference where he spoke about having students in his college-level classes required to fail before they could earn an A in his class.  In his August 2012 essay “Teaching to Fail” from Inside Higher Ed (posted at 3:00 am, which I thought was kind of funny), he talks about attempting to make a rubric for the “quality of failure” on how well a student had failed at a task.  I thought this was an interesting concept.  I mean, in order to fail well, can’t you just really screw up, like not do it at all?  Prof. Burger states that allowing students to freely reflect on their “false starts and fruitful iterations” as well as how their understanding “evolved through the failures” can be extremely beneficial.  He also states:

“To my skeptical colleagues who wonder if this grading scheme can be exploited as a loophole to reward unprepared students, I remind them that we should not create policies in the academy that police students, instead we should create policies that add pedagogical value and create educational opportunity.”

Last year for the first time, I tried a similar experiment wherein I gave students an assignment to write a paper in my honors geometry class.  They had to choose from three theorems that we were not going to prove in class.  However, it was clear that they could obviously just look up the proof on the Internet or in a textbook or somewhere, since they clearly have been proven before.  The proof was only 10 or 20% of their grade.  The majority of the paper’s grade was writing up the trials and failures in writing the proof themselves.  This proved to be one of the most exciting projects of the year and the students ate it up.  I even told them that I didn’t care if they looked up the proof as long as they cited it, but I still had kids coming to me to show my how they were failing because they wanted a hint in order to figure it out themselves.  It was amazing.

This past week I showed my classes Kathryn Schultz’ TED talk entitled “On Being Wrong” in which she talked about the ever popular dilemma of the Coyote who chases the Road Runner, usually off a cliff.

My students loved her analogy of the “feeling of being wrong” to when the Coyote runs off the cliff and then looks down and of course, has to fall in order to be in agreement with the laws of gravity.  However, I proposed a different imaginary circumstance.  Wouldn’t it be great if we could run off the cliff, i.e. take that risk, and before looking down and realizing that vulnerability and scariness, just run right back on and do something else?  No falling, no one gets hurt, no one looks stupid because you get flattened when you hit the ground?  Maybe that’s not the “feeling of being wrong” but it’s the “feeling of learning.”

Next blog entry on creating the classroom culture for “defying gravity.”

Doing What You Can

I just got back from a great visit to Toronto (which was also my first visit to that wonderful city.)  I spoke at a conference and also did some work at beautiful girls’ school there that was interested in PBL.  It was the first time where two of my research interests intersected (Gender and PBL) and it was fascinating for all that were involved – quite wonderful and so much fun.

Many teachers talked to me there (and it comes up everywhere I go) about the fact that they are the only teacher, or one of the few, at their school that is interested in  trying out this different method of teaching, but need to keep up with the syllabus that their colleagues are using in order for students to be prepared for the common exam either at the end of the term, the end of the semester or even on a monthly basis.

This can be problematic when there are school districts that dictate down to the homework assignment or classroom activity that you need to be doing on a daily basis.  The free that classroom practitioners need to make decisions about what is best for the learning of their students is quite important.  However, it is still possible to integrate problem solving or methods of PBL into your classroom when you can get.

I talk about the Continuum of PBL when I give workshops to let people know that you don’t have to dive in head first if you want to try your hand at classroom discourse a little at a time.  Learning to facilitate discussion as a long-time direct instruction teacher is actually quite difficult to allowing students to have more authority can be tricky.  Here is the visual aid that I use when I discuss it:

“A Continuum of PBL” cschettino 2013

The arrow tells you the level of decompartmentalization of topics – in other words how the topics are blended together or not.  In a traditional mathematics curriculum, a textbook artificially separates mathematics into what I like to think of a “compartments” that in a very linear order and most students learn to believe that mathematics must be taught in that order.  Yes, some operations and skills must come before others, but conceptually a great deal of mathematics can be learned or thought about in no particular order.  It is all extremely and equally fascinating.  In a whole problem-based curriculum such as what the faculty at Phillips Exeter Academy has written there are no chapters that mark the ending of the content and the beginning of another since there truly no time when that content is no longer applicable to the new material that is being learned (yes, of course that is true in a text book as well, but the chapter alone have come to imply that to students).

Decompartmentalization can come at different levels.  At the lowest level,many  teachers use “Problems of the Day” that challenge students at the beginning of class with logic puzzles, topics they are not seeing regularly or interesting tidbits like soduku or other fun activities to get students’ minds working.  These create discussion and allow them to see problem solving in action.  However, there is little connection to the mathematics that is being learned in the class proper.

I won’t discuss every type of PBL on the continuum or this will turn into one of my hour long talks, but I will say that if you are interested in attempting to keep up with your colleagues who are following a traditional syllabus but you might want to use less direct instruction I have a link to my “Motivational Problems” page in order for you to have them start the conversation based on their prior knowledge of material.  The problems are listed by topic and you can have them move forward in class by presenting problems and then have them practice with problems in the textbook.  Anyone who tries this – I’d love to hear from you!

This was how I first started at my last school and it worked well for me.  You can read my article from 2003 in the Mathematics Teacher to learn what it was like.  But it definitely moved me in the right direction.  Keep pushing on!

An infinite amount of thanks…

Everyone has those mentors in their life who have impacted their work or career in ways that have truly changed who they are.  In my instance, the person I am going to write about not only has impacted my life and career, but because he taught me so much about great teaching, in particular PBL, he has impacted all of the students and teachers I have worked over my twenty year career so far.  So I feel justified in taking a short break from writing strictly about professional educational work musings and just finding a moment to say thanks for the life and work of Rick Parris.

Even if you never met Rick in his time teaching at Phillips Exeter Academy, or used his wonderful opensource Peanut software for windows machines, or downloaded the faculty-authored materials that he was integral in writing by the mathematics department at PEA – if you have worked with me at all, you have been affected by Rick’s work.  Rick Parris had to be one of the most brilliant, efficient, insightful  mathematicians I’ve ever been lucky enough to work with.  He saw things in a problem that I definitely never would be able to see in a million years.  I was so extremely intimidated by him when I first started working in the same department that I would go for days confused about a problem instead of go up and ask him.  But what I soon found was that not only was he one of the most brilliant mathematicians, I’ve ever met, but he was one of the best teachers too.  Now, there is a rare combination – finding someone who has the insightful intelligence to be able to have a Ph.D. in mathematics but to also be so sensitive to others’ understanding of the subject and the patience and passion to want them to love it as much as he did.

I remember finally having the courage to go and ask him a question about a problem in the 41C materials on fall afternoon (mostly because I knew I had to understand it) and he looked at me, with what I thought was a look of disdain or horror that one of his colleagues wouldn’t understand a problem that he wrote.  And just as I was going to run in shame, he said something like, “that is such an interesting way to look at that” and I was amazed at how good that felt.  He entertained my ideas and although I felt like he was initially just appeasing me, I soon realized that he was truly and sincerely intrigued.  Our relationship as colleagues and interested problem solvers grew, even after I left PEA.  He allowed me to keep in touch constantly asking him questions and posing them over email.  He taught me so much about writing great problems, encouraging students to ask great questions and making sure that they always felt like they were they most interesting questions ever.

This past summer, the last time I saw Rick, we were talking about the game of Set (you know that really fun card game with the colors, shapes and numbers).  We were just posing really fun questions like “What’s the maximum number of sets you can get in a 12 card deal?”  We found these types of questions intriguing and even after we parted company we continued emailing with email subject lines like “a baker’s dozen of sets”, “set lore” and “the game of set redux.”  He always treated me like a real mathematician even though he was the one who I saw as my inspiration and motivation in that area.

Rick taught me about how to scaffold problems (not too much) so that students would see their way through a topic and find out exciting ideas of mathematics on their own.  I loved to watch him teach, probably observing his classes three or four times a year in order to gain insight into his questioning methods.  He made a point of trying to hear from every student in the class at least once a class.  I don’t know if he ever knew how much of an impact he had on my teaching and philosophy of learning.  I am so grateful.

So how do you say thank you to someone who pushed you in a direction that changed your life?  I guess I have just to recommit myself to learning about and researching the best practices of inquiry and problem-based learning in secondary mathematics education.  I do believe that the world needs to know about the contributions of this man and the department at PEA because without them and the model that they have created, I’m not sure that many of the schools today that utilize their curriculum would be where they are.  I give thanks to Rick and consider myself extremely lucky to have worked with him and shared his enthusiasm for problems.

Documents for Anja S. Greer CwiC sessions

I’ve decided to post the presentation slides and handouts for the CwiC sessions that I’m giving at the Exeter Conference here.

Here is the handout for my CwiC Session entitled iPad Apps for the Mathematics Classroom:
handout .

Here are the presentation slides for the same CwiC Session:
Slides .

Here are the presentation slides for the Calculus of Friendship quick session: (the one with the solutions will be up after the conference)
Slides .

Here are the presentation slides for the session on Teaching STEM for Girls:
Slides .

Boston College Discrete Math Conference

Thanks to everyone who attended my presentation today at the Boston College Discrete Math Conference. For those of you who wanted presentation slides, here they are .

Thanks to the participant who helped edit my error on the matrix worksheet. Here are the problems that we discussed and some motivational problems. Enjoy!
– Discussion problems from the slides
– Motivational Problems on Matrices
– Motivational Problems on Apportionment

If you are interested in the PBL Geometry curriculum I spoke about, look for it under In the Classroom->Teaching in the menu above.