Category: Articles

The Downside of Naming “Feminine” Traits

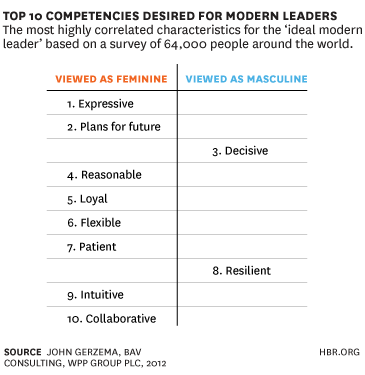
I recently read this article from the Harvard Business Review stating that “Feminine” Values Can Give Tomorrow’s Leaders an Edge.   A study was done asking 64,000 people from over 13 countries all over the world for the traits, skills and competencies that were perceived to be appreciated in leaders in the world of business and leadership.  The conclusions (from statistical modeling) that the analysts came to were that tomorrow’s leaders must overwhelmingly learn to have what our culture has defined to be “feminine” traits.  Here’s the list of the survey said were the top 10 desired traits for modern leaders:

 

I don’t disagree with these traits, honestly, and as a feminist it actually excites me that the values that I work to foster in the classroom are being valued in the boardroom and society in general (Dewey would be proud too).  However, something that is troubling me is the ever-popular dichotomy that is being set up here that seems to always be at the heart of many issues that rise in our society.  Something I wrote about in my dissertation and any time I talk about Relational Pedagogy is the idea of breaking down this concept of masculine vs. feminine thinking, not only in mathematics or education, but in human relations altogether.

I will be the first person to motivate and encourage young women in the STEM fields or take a young boy who likes cooking and say, “you, go guy” and hand him an apron – but that is about individualism and allowing young people to be who they want to be and feel empowered.  In my classroom, allowing students to see multiple perspectives and have their voice heard whether they are male or female is entirely my top priority because they are individuals and their relationship with mathematics is unique.  For a long time in math education, the ideas in this study were how young girls were viewed – researchers thought that if we just saw how girls were different from boys that we could see why they weren’t “doing as well” as boys.  However, we saw that they were doing just as well.

So my problem with this study is not the fact that women will be empowered to become leaders in business – no, that’s really exciting to me.  In fact, maybe some men will see the potential in women and decide to hire more women in the future and this will create more jobs for women and this will in turn, create a more equitable workplace and more favorable working conditions, which will then create more exciting options for business situations because of the fact that different perspectives are being looked at with such different views being taken in problem solving in business.  That is extremely exciting to me!

However, my problem with this study is this.  In order to make such radical changes in how people view gender differences in our society we really need to stop making such huge oppositional statements.  In support of this view, Mendick (2005) stated

By aligning separate-ness with masculinity and connected-ness with femininity, these approaches feed the oppositional binary patterning of our thinking and in the final analysis reiterate it (p 163).

If we just continue to point out how “unfeminine” men are because they are less expressive and how “unmasculine” women because they can be undecisive all we are doing is perpetuating the oppositions that separate us instead of our humanness that can bring us together as learners and our vulnerability that can help us problem solve with our strengths and weaknesses that will make us stronger if we work together.

There was an article published in 2010, about how if you put more women in a group of people the “collective intelligence” increases – the group works better together.  I’m sure there’s some tipping point though that if the group has all women there are diminishing returns for this measure.  There has to come a time when we value the relationships in our learning, our work and our classrooms and as teachers foster all of these traits to the best of our abilities.

Teaching Students to Become Better “Dancers”

So the other day I read a tweet by Justin Lanier that really sparked my interest.

 We all know the scenario in classroom discourse where a student asks a question – a really great question – and you know the answer, but you hedge and you say something like, “That’s a great question! I wonder what would happen if…”  So you reflect it back to the students so that they have something to think about for a little while longer, or maybe even ask a question like “Why would it be that way?” or “Why did you think or it like that?”  to try to get the student to think a bit more.  But what Justin, and the person who coined the phrase “authentic unhelpfulness” Jasmine Walker (@jaz_math), I believe were talking about was hedging because you really don’t know the answer – sincere interest in the uniqueness of the question – not because you’re so excited that student has helped you move the conversation forward, but because of your own excitement about the possibilities of the problem solving or the extension of the mathematics.

I think what got me so excited about this idea was how it connected to something that I was discussing earlier this summer with a group of teachers in my scaffolding in PBL workshop in late June.  In a PBL curriculum, the need to make sure that students have the right balance of scaffolded problems and their own agency is part of what Jo Boaler called the “Dance of Agency” in a paper she wrote in 2005 (see reference).  My understanding of this balance goes something like this:

(c) Schettino 2013

So initially, the student is confused (or frustrated) that the teacher refuses to answer the question although you are giving lots of support, advice and encouragement to follow their instincts.  The student has no choice but to accept the agency for his or her learning at that point because the teacher is not moving forward with any information.  But at that point usually what happens is that a student doesn’t feel like she has the authority (mathematical or otherwise) to be the agent of her own learning, so she deflects the authority to some other place.  She looks around in the classroom and uses her resources to invoke some other form of authority in problem solving.  What are her choices?

She’s got the discipline of mathematics – all of her prior knowledge from past experiences, she’s got textbooks, the Internet, her peers who know some math, other problems that the class has just done perhaps that she might be able to connect to the question at hand with previous methods that she might or might know how they work or when they were relevant – that discipline has had ways in which it has worked for her in the past and lots of resources that can help even if it may not be immediately obvious.

But she’s also got her own human agency which is most often expressed in the form of asking questions, seeing connections, drawing conclusions, thinking of new ideas, finding similarities and differences between experiences and thinking about what is relevant and what is not.  These pieces of the puzzle are not only important but a truly necessary function of the “dance of agency” and imperative to problem solving.

Interweaving both of these types of agency (and teaching kids to do this) have become more important than ever.  Yes, being able to use mathematical procedures is still important, but more important is the skill for students to be able to apply their own human agency to problem and know how and when to use which mathematical procedure, right?  This “dance” is so much more important to have every day in the classroom and if what initiates it is that deflection of authority then by all means deflect away – but the more we can “dance” with them, with “authentic unhelpfulness” and sincere deflection because we need to practice our own human agency, the more we are creating a true community of practice.

Boaler, J. (2005). Studying and Capturing the complexity of practice – the Case of the ‘Dance of Agency’

Be the Change You Want to See

I just finished listening to a great “blogcast” that Tony Wagner gave as an interview for Blogtalkradio about his new book “Creating Innovators:The Making of Young People Who Will Change the World.” Kind of a neat idea for a book in which he has done some great research looking into how some new ideas got started by young people, how their creativity was fostered in their childhood, parenting and education, etc.  Definitely worth taking a listen to.

Listen to internet radio with Steve and Mary Alice on BlogTalkRadio

One of the things that Prof. Wagner talks about in his interview is the idea of fostering the creativity that leads to innovation.  As he spoke to these great innovators that he interviewed, they could all name at least one teacher in their career who had a “significant impact” on their learning.  Interestingly, the characteristics of that teacher were often very similar, Wagner said.  They were known for encouraging collaboration and often assessing it, creating a classroom that was often interdisciplinary and problem-based (of course) and empowered his or her students to be creative in their problem-solving and make mistakes.  Why is this not surprising?  To all of us who strive to foster the practice of creativity and hope to allow our students to become innovative and original thinkers, we have known that these are the values that we should uphold in the classroom. I’m so glad that Wagner did this great research and wrote this wonderful book.

However, we also know the realities of the limitations that many of us teachers have that come with the system within which we teach.  I have spoken to so many teachers from around the country who, with all good intentions are striving to make their classrooms more problem-based and encourage creativity.  They are truly trying to be the change they want to see in mathematics education today.  But the fear of standardized testing that is not assessing these values, affecting their evaluations or public awareness of parental or administrative dissatisfaction or vocal disagreement with these goals, needs to be balanced with a teacher’s desire to move ahead.  Limitations of a teacher’s time, energy and their own creativity keep them from being able to proceed without support from like-minded colleagues and leaders in their district.

At the end of the interview, Prof. Wagner talks about his move from the Harvard GSE to his new position in the Technology and Entrepreneurship Center at Harvard.  He says something like he’s found that he doesn’t belong in a school of education because he’d like to be somewhere where the focus is “explicitly on innovation.”  My question is why can’t that be a school of education? or a school at all?  Why can’t learning be explicitly innovative and thought about as innovation in general? I believe all of us are capable of thinking of our schools as places of learning where students are being innovative as they learn.  Every day I ask my students in my classroom to attempt to think of something new to them.  It may not be innovative to me, but as long as it is in their eyes and their brain is attempting to see something in a new way on their own, I believe they are being innovative.

I would encourage us all to continue to be the change that we want to see in schools and not try to find other places where we think we belong.  It’s so important that we continue to make these changes no matter how small and I hope to continue to be a resource in your own classroom innovation!

Affirming the “Un-fixing” of the roles in Mathematics

So after nine, long hard years, I am finally at a point where I am proud to say, “I’m finished!”  Woo-hoo and hurrah, tonight I will submit my dissertation electronically and you can call me Dr.  Reading over my work has been probably one of the most fulfilling acts of my professional life, as was defending my dissertation last week.  I can’t believe how fun it actually was – too true.  When you are passionate about a topic, it never gets old. Then, just today my advisor sends me an article that was published in the Harvard Education Letter titled, “Changing the Face of Math”which strangely sounds so much like what I’ve been working on for so long.  It talks about the current state of the way students create identities in mathematics in the U.S. and how this is detrimental to their beliefs about what they can do and be in the mathematics classroom and beyond.  Sadly, as high school teachers, half of our job is undoing the mathematical identity that the system has put in place all the years before they have come to us. In my dissertation, I wrote about not only this identity question but the difficulty in how American society has such a gendered, dichotomous view of mathematics that even those of us who attempt to move past the stereotypes because of our love of mathematics end up with difficult situations to work against.  For some, it is so difficult that we end up giving up and choosing the easier path – the girl who loves physics but choose biological engineering because she feels like she belongs there.  Or the young woman who goes to college to be a math major, but ends up in International communications because the classes were not taught in a way that worked for her learning style.  Or the weak female mathematics student who doesn’t even consider taking another math class in college because of the negative view of her abilities years ago. In this article they say,

“Math education experts say we’re in crisis and that traditional approaches of treating math like a cold-blooded subject amid the warm and engaging world of K–12 schooling are a big part of the problem. Narrow cultural beliefs about what math success looks like, who can be good at it, and what it’s used for are driving students to approach the subject with timidity—or not at all.”

Which was so affirming because it was the major educational research question that motivated my dissertation!  I love it.  Allowing all underrepresented students, not just girls to find ways to change the way they view themselves as math students by changing the way we teach mathematics would be revolutionary, and so many people are doing it.  I am proud to be a part of this movement to “unfix” the gendered, dominant, presumed ways of mathematics learning and open it up to more subjective, creative and collaborative thinking processes. It’s a great time to be a revolutionary!

Creating a Conspiracy in the PBL Classroom

Any Mad Men fans out there?  I just love some of the characters and the struggles they put themselves through.  In one episode from season 5, called “Signal 30,” Lane Pryce needs to take some clients out to dinner and Roger Sterling is giving him some advice on how to woo them to sign a contract with Sterling Cooper Draper Pryce.  Since he is not an account man, Lane is nervous about landing the account.

Roger:  And then it’s kind of like being on a date.

Lane:  Flattery, I suppose…

Roger:  Within reason, but I find it best to smile and sit there like you’ve got no place to go and just let ‘em talk.  Somewhere in the middle of the entrée, they’ll throw out something revealing and you want to wait ‘til dessert to pounce on it. You know, let him know you’ve got the same problem he has.  Whatever it is, and then you’re in a conspiracy – the basis of a quote “friendship”.  Then you whip out the form.

Lane:  What if I don’t have the same problem?

Roger:  It’ll probably be something like he drinks too much, he gambles…I once went on a five minute tear about how my mother loved my father more than me and I can assure you, that’s impossible.

Lane:  Very good then, and if for some reason he’s more reserved?

Roger:  You just reverse it – feed him your own personal morsel.

Lane:  Oh I see.

Roger: (getting up to leave) That’s it, get your answers, be nice to the waiter and don’t let him near the check.

My husband and I watched this episode about the same time I was having a great deal of resistance in my class to PBL.  I was talking to my husband about how to get students to buy into the notion of learning for the sake of learning where everywhere else in their lives what measures their learning are their grades.  Why would I expect anything different from them if this is the culture they were brought up in?  They depend on their grades to get them into a good college and if their grades are not up to a certain standard, they will not “measure up.”

I get this question all the time from other teachers – about  how to motivate students to find the love of learning and the interest in problems when they do not necessary know the solution methods to find them.  I usually tell them the same things – talking about the values of the class, grading class contribution with a viewable rubric,  grading their metacognitive journal writing, rewarding them with an interesting relationship with a great teacher…OK that might be pushing it.

However, this year is different.  I am having the hardest time trying to let them know what I want from them.  They do the homework, try their best, write down notes, but for some reason it feels different.  It’s almost as if there’s this wall between them and me and I don’t know how to get them to see my side.  I have had this problem with students in the past, but usually with a whole class.  Some of them blatantly are interrupting each other and others are obviously ignoring each other.

Then my husband says, “Maybe it’s like the conspiracy.”  I said, “What?” He said,” You know, what Roger was talking about on Mad Men.  Now, Roger Sterling is no saint (those of you who watch the show know this all too well) and I usually take what he says with a grain of salt.  I also would not ever consider taking advice from him, especially about teaching, but I allowed my husband to continue.  He said maybe what I had to do was build up the conspiracy that Roger was talking about.  I had a real problem with that because I am so committed to relational pedagogy that there’s no way I could lie to or mislead a student about their learning.  But that’s not what he really meant.

I suddenly realized that what had happened was I was teaching a curriculum that I didn’t even buy into.  I had just finished teaching them matrices and matrix operations with some problems that I had written, and it went very well.  However, in the end I did have to do Cramer’s Rule and determinants.  I tried motivating the problems about determinants with the area of a parallelogram, which kept them interested for a while, but in the end, with a 3×3 it was just here’s the way to do it.  I’m not sure that I could’ve expected them to have enough prior knowledge to derive the formula for finding a determinant of a 3×3.  As much as I tried to cover it up with problem-based learning, it was still a curriculum that is antiquated and not necessarily what I felt they should be doing and learning.  I couldn’t hide it any longer.

But we’re caught aren’t we?  Do we change the whole system – college prep curriculum, SAT required math, college expectations – and if so how do we do that? (see ahbel.com for a great article on this and a keynote address called Reflections on a 119 year old curricullum!)  Do we move beyond the required standardized testing material and allow our students to see mathematics the way we see it?  Yes, that’s the conspiracy – that’s what my husband was talking about.  When kids complain to me, I will “smile and sit there while they talk” knowing that I’m going to try to get something that we have in common.  “Do you hate solving a system of three equations with three unknowns with a determinant? Oh yeah, I did too in high school.  Wouldn’t it be great if we could do something else?  What else should we do?  Let me find some other problems that might be interesting.”  We have the same problem (literally and figuratively), now we’re on the same playing field having similar motivating factors.

And you know what?  I don’t think it would be the end of the world if they’re not revealing and you reversed it.  We are allowed to say to them that we don’t understand why we are still teaching this and these would be my reasons for taking it out of the curriculum – part of your own personal morsel.  It might actually bring you closer as a class and have you talking about how your hands are tied and we have to get through this “together.”

Yeah, there are little tricks that can be learned and carrots that can be used to get students to do what you want them to do, but in PBL, that’s not the point.  There is very little for them to mimic because it is based on their prior knowledge.  They are the ones who need to move the curriculum forward.  So in a nutshell,

  1. Take action – Get to problems in order for students to start feeling empowered and active in class.  Once they see that they are capable of a great deal on their own, it is amazing what they can accomplish.
  2. Create relationships – be sure that you are being reciprocal in your attempts at problems and valuing theirs.  The concept of Relational Trust and Authority are huge parts of a PBL pedagogy (Boaler, Bingham)
  3. But make sure that you are at least somewhat in control in the end because we are, at least for now, still responsible for making sure that some understanding of what we might consider unnecessary skills, for their next courses or future use.

As Roger said, “Get your answers, be nice to the waiter and don’t let ‘em near the check.”  Create that conspiracy.

 

 

 

Defying Gravity as a Means to Learning from Mistakes

There’s a lot of blogging, writing and research (and anecdotal stories) out there these days about trying to foster the value in students for the appreciation in failing.   I even wrote a blog entry two years ago entitled “modeling proper mistake-making” way before I read anything or watched any videos on the Internet.  From teaching with PBL for over 17 years, I am a pro at making mistakes and watching students struggle with the concept of accepting the idea of learning from their mistakes.  This is so much easier said than done, but it is clearly something that grow to love even if only for a short time.

Last April, I had the pleasure of hearing Ed Burger at the NCTM national conference where he spoke about having students in his college-level classes required to fail before they could earn an A in his class.  In his August 2012 essay “Teaching to Fail” from Inside Higher Ed (posted at 3:00 am, which I thought was kind of funny), he talks about attempting to make a rubric for the “quality of failure” on how well a student had failed at a task.  I thought this was an interesting concept.  I mean, in order to fail well, can’t you just really screw up, like not do it at all?  Prof. Burger states that allowing students to freely reflect on their “false starts and fruitful iterations” as well as how their understanding “evolved through the failures” can be extremely beneficial.  He also states:

“To my skeptical colleagues who wonder if this grading scheme can be exploited as a loophole to reward unprepared students, I remind them that we should not create policies in the academy that police students, instead we should create policies that add pedagogical value and create educational opportunity.”

Last year for the first time, I tried a similar experiment wherein I gave students an assignment to write a paper in my honors geometry class.  They had to choose from three theorems that we were not going to prove in class.  However, it was clear that they could obviously just look up the proof on the Internet or in a textbook or somewhere, since they clearly have been proven before.  The proof was only 10 or 20% of their grade.  The majority of the paper’s grade was writing up the trials and failures in writing the proof themselves.  This proved to be one of the most exciting projects of the year and the students ate it up.  I even told them that I didn’t care if they looked up the proof as long as they cited it, but I still had kids coming to me to show my how they were failing because they wanted a hint in order to figure it out themselves.  It was amazing.

This past week I showed my classes Kathryn Schultz’ TED talk entitled “On Being Wrong” in which she talked about the ever popular dilemma of the Coyote who chases the Road Runner, usually off a cliff.

My students loved her analogy of the “feeling of being wrong” to when the Coyote runs off the cliff and then looks down and of course, has to fall in order to be in agreement with the laws of gravity.  However, I proposed a different imaginary circumstance.  Wouldn’t it be great if we could run off the cliff, i.e. take that risk, and before looking down and realizing that vulnerability and scariness, just run right back on and do something else?  No falling, no one gets hurt, no one looks stupid because you get flattened when you hit the ground?  Maybe that’s not the “feeling of being wrong” but it’s the “feeling of learning.”

Next blog entry on creating the classroom culture for “defying gravity.”

The Role of Technology in Relational Pedagogy?

So I’ve been thinking a lot lately about technology and learning.  There’s so much in the news about MOOCs, using iPads, schools using technology, etc.  I am even part of a pilot program at my school right now where all of my students have iPads in my honors geometry class and we are trying to communicate at night using Voicethread and the iPads.  My hope was that having a way to share ideas during the evening would lessen the stress of homework problems that students are asked to grapple with in the PBL curriculum would give them more opportunities to throw out problem-solving ideas with each other before class starts so that we would spend less time in class debating different methods of solving the problem (although that’s what I love about class, right?).

But I’m asked as a teacher to find ways to integrate technology into my classroom – but to what end?  I want to find ways to use technology to solve problems, to explore ideas and to help improve students’ understanding of the mathematics.  Not necessarily help them communicate with each other, which is what I’m finding most of the apps out there are for right now – which I am open to – but they are removing a huge part of the learning triangle.  In fact, David Hawkins (1974) wrote about the I-thou-it reciprocal relationships in learning that simply must exist between the learner, the teacher and the subject matter.  He said that if one of the relationships is hindered or dysfunctional in some way, that learning is not optimal.

Hawkins (1974)

So if I interrupt that relational triangle between the students’ communication with the material (and with each other) and with me, using technology instead of discussion and the connection with all three, my fear is that learning is not optimal.  Perhaps the technology could enhance it, but for now I see that it is not truly happening.  My guess is that it has to take time for the students maybe to want for that to happen.

I also just read an article on Edutopia by a guy named Matt Levinson that was entitled “Where MOOCs Miss the Mark: The Student-Teacher Relationship” where it was stated that a lack of mentorship, close guidance or meaningful relationship between teachers and students is what is really lacking in these online courses. Even students who use Khan Academy lectures for “learning” sometimes comment that even though they don’t like sitting and listening to lectures in math class, they would “much [prefer] listening to her math teacher explain the same concepts because she likes this teacher and feels comfortable asking questions and going for extra help outside of class.”

Carol Rodgers (one of my most favorite people on earth) writes about teacher presence and the importance of it in the classroom.  I believe in mathematics class and especially the problem-based mathematics class it is truly essential because in order for students to take a risk with a method, they need to feel supported and safe in order to be open to new ideas and to discuss them with others.  With the open presence of a teacher and mentor, students are not “receiving knowledge” but creating it with others – creating it within those relationships that Hawkins was talking about – maybe with technology or without it.  But  for someone who just spent two years writing about the importance of relational pedagogy in PBL, I find it extremely difficult to assume that without those relationship the same exceptional amount of learning would go on.

Wrong is not always bad

I recently read an article in Education Week that was proclaiming the benefits of discussing student mistakes in class. The author, Alina Tugend who has recently published a book entitled, Better by Mistake: The Unexpected Benefits of Being Wrong, cited that in some asian cultures students can be asked to work out “math problems in front of the whole class for a healthy period of time…even if [they] are doing it wrong.” She goes on to discuss that the teacher might ask the student to discuss her thought process and why they chose to do the problem that way and the decisions they made at certain points in order for the class to see the choices that were made at certain crossroads in the problem solving process. Some researchers believe that this type of discussion allows students to help create a sort of “index” of what still needs to be learned or what has already been learned.

In other words, the class is actually viewing the errors and misunderstandings as a helpful thing. They’re using the opportunity of the mistake, of being wrong, as kind of a check point to see what else they need to know. Perhaps someone else in the room might have did something differently that might have led them in a direction that was more fruitful and everyone can learn from that as well. So there is much more to be learned from this type of environment. On the one hand, the students learn the material, but on the other hand, they are learning that they can learn from each other and they learn that being wrong in the first place was actually helpful.

This also goes to the idea of how problem-based learning is ideal for this type of learning. Posing the problem in the context of a prior knowledge base, allows students to think that they have a background that is sufficient for them to do the problem, they just need to recall what that was with a little push. It also fosters was researcher Carol Dweck calls the “Growth Mindset” allowing students to believe that their intelligence and ability to succeed to flexible and not pre-determined.

I am getting excited for my course next week at the Math and Technology Conference in Exeter, NH which I believe is full. I love this conference because I always meet lots of people who are so eager to engage in mathematics and learning. It should be a great time of dialogue and I look forward to a great time!