Sometimes my ignorance with respect to Twitter just floors me. Today alone I made two huge faux pas (is that plural?) with two people that I really respect and just made a fool out of myself – typos, misinterpretations, and misunderstandings abound in my tweets. But I have to say I press on – because I have found so much that informs my teaching and learning that I can handle the fool-making and embarrassment.
So here’s one thing that I did a few weeks ago – someone tweeted about this great article that I, of course, then went and read, took a picture of the great diagram in the article – but forgot to “like” or “favorite” or whatever it’s called now. So now I can’t give credit to whomever brought me to this wonderful enlightenment about which I will now write. So if you are reading, sir/madam, who tweeted this article, please forgive me.
I read this short blogpost entitled “Brennan’s Hierarchy of Imagination” and immediately made the connection to PBL.
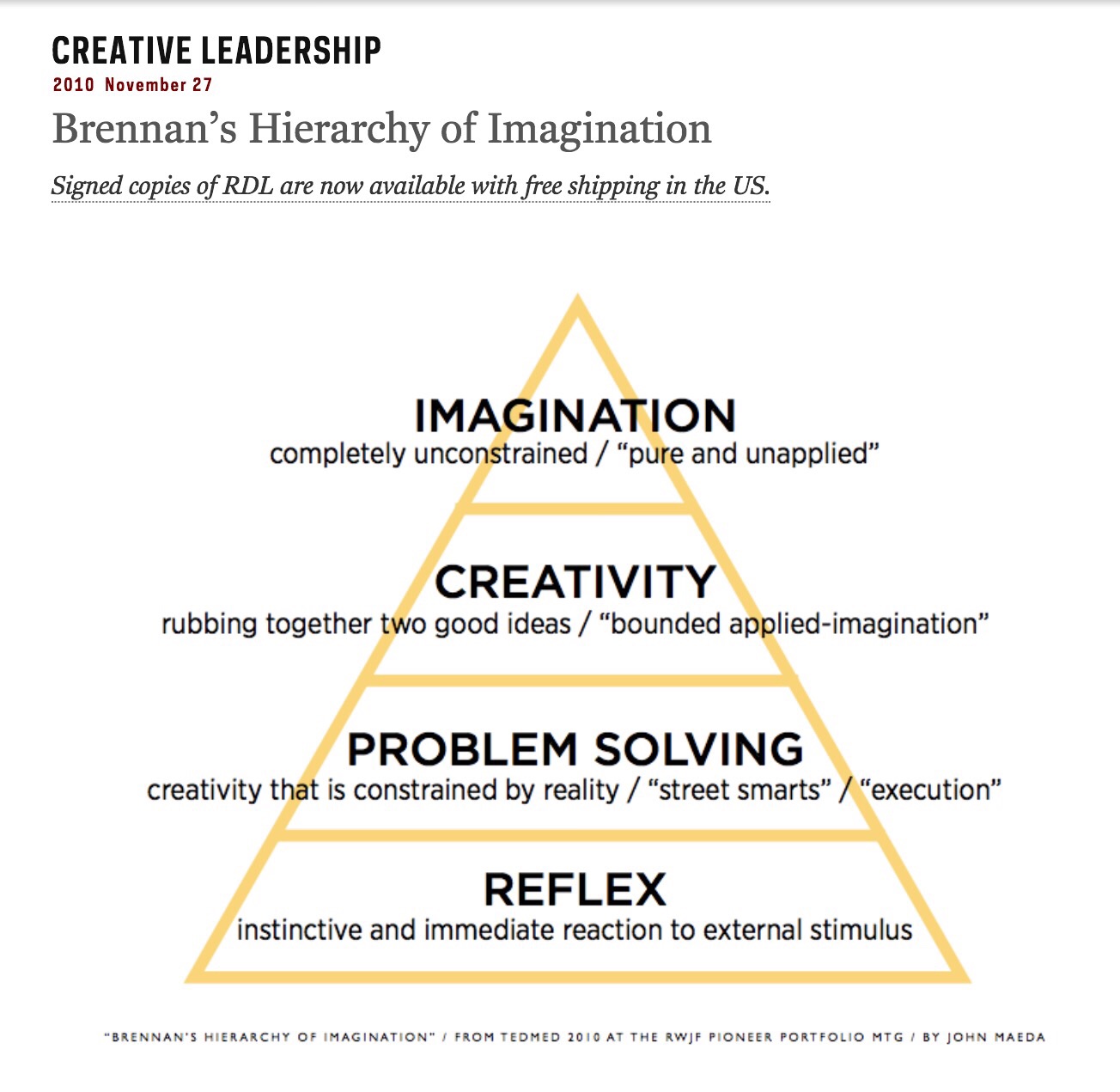
The author, John Maeda, wrote about a conversation he had with Patti Brennan about Maslow’s famous Hierarchy of Needs of students in their learning. These two were talking about the fact that teaching creativity is really hard and Patti Brennan was thinking that it was a bit easier to teach someone to use their imagination. She was talking about this in the context of the health care field – trying to help people empower themselves to help themselves.
Of course, the first thing I thought of when I saw this pyramid was problem solving. I thought this was brilliant! The foundational, lower level of reflex or instinct is analogous to doing problems that you have seen before. Students love this instinct – the idea that if you can do a problem that someone has shown you how to do, that you are problem solving, – it gives them a reaction of completing something, some kind of satisfaction.
The next level which is appropriately called problem-solving is when you are actually solving a problem that has occurred but is constrained and you are executing skills. I love this. It still takes some talent and analysis, but you are still just reacting to a given situation. Perhaps putting together two different methods that someone showed you and seeing what happens?
The third level that she calls creativity is the first step to unique ideas and methods. The first attempt at doing something in a different way – saying what if we tried this? Has anyone every done this before? Why not? It’s still bound by the reality that we experience, but seeks to move past the knowledge that we have.
And finally imagination is what I think happens when my 4-year-old niece explains how the clouds got up in the sky because the stars moved so fast pieces came off and clumped together, or when a student can’t figure out if there are more real numbers between 0 and 1 as there are integers and they try to describe the size of those sets to me with things they imagine.
If I’m lucky, I’d say some of the kids in my classes get to creativity – in fact I think that’s been my goal as of late. To get them at least to experience it with some projects, assignments and good problems. To get them to realize that mathematics is more than just a reflex or even just reiterating a process.
Hopefully, this coming year the number of kids who will get to that third level will increase, but who knows? I do love this framework because at least I know I don’t want them stuck on that bottom level for level for long.
I’ll be happy if I can get every student to problem solving. Though creativity and imagination are joys to behold.
I hadn’t thought about it as a tower of dependencies before. hmm
Thanks for reading Alice! Sometimes creating a framework for larger ideas like make things more complicated but sometimes they simplify them while at the same time give teachers ways of talking about very abstract skills like problem solving.