Author: Carmel

Blog Challenge Day 3: Do I really practice what I preach?

So the question for today is “Discuss one observation “area” that you would like to improve upon for your teacher evaluation.”  This is a tough one for me because as a teacher at an independent school formal evaluations are done in the second and sixth years so I don’t have formal evaluation “areas” per se.  Last year, I had a colleague sit in on my classes and give me feedback over a month’s period  and it was extremely helpful to have his perspective.  I also have many teachers come from other school at different points in the year in order to learn about problem-based learning, so I am used to having people in my classroom, but I haven’t really asked for feedback in one particular area in very long time.

However, I do believe that something I wonder about when I speak to teachers learning about PBL is how well I really facilitate PBL discussions.  I know what I’m supposed to do but the time constraints and the issues of adolescent life often keep me from being the best I can be.   I know I can be hard on myself, but if I had an expert in questioning, wait time, reactions to statements, inquiry and scaffolding who could come in and watch me teach for a week or so, that would probably be the best thing for me right now.  It would be so helpful.  So if anyone is willing…please get in touch!

Blog challenge Day2: New Technology for Collaboration in PBL

For the past two years, I have been lucky enough (or unlucky if you are less inclined to use technology) to have classroom sets of iPads for my geometry classes and have been able to experiment pretty easily with some different ways of teaching – collecting homework electronically (that was a fail), using Geogebra and Notability to get some really nice diagrams (that was pretty great!) and working with Voicethread to have students collaborate at home during homework. I gave a CwiC session talk last year at the Anja S. Greer conference on my use of Voicethread as a means of collaboration in problem solving and it went over really well. Here’s an example of how students used it:

So since I felt like that was so helpful as a discussion forum in the evenings (and also allowed more time in class for discussion the next day), I wanted to find other apps that might be just as helpful.  One of the things kids didn’t like about Voicethread was that it forced asynchronicity – there was no way to talk to someone online.  In fact, what sometimes happened was that a student would post a question and no one would respond until maybe 11 pm, and then by that time they might’ve gone to bed or moved onto their French homework or something.  Bummer.

So now this year I’m going to try a new app called Talkboard.  This is a really cool app that allows a student to send an IM or email to another student (or more than one) and then have a conversation (with voice) while also seeing writing and drawing real-time.  These synchronous discussion are kept in “projects” that can be saved and even exported as a pdf (without sound sadly) but there can be a record of their ideas.  Students can come to class the next day with some work on the iPad that contains the ideas they had for the problem solving process.  You can keep adding pages to the project and you can also import pictures – like graphs and diagrams from geogebra or desmos.  So I’m pretty pumped to try this out.

If anyone has used this app and has some experience with it, I’d love to hear about it!  Thanks so much!  …and happy experimenting!

TeachThought Blogging Challenge Day1: Goals for this Year

 OK, so I’ve decided to try to blog more this coming year (like I don’t have anything else to do working at a boarding school) and I happened to run across the TeachThought Blogging Challenge the other day, so I thought I would try to see how many of the 30 days, I might be able to actually write something that was worthwhile.
 
 I even downloaded a new app for my iPad to make blogging easier (we’ll see if that prediction comes true or not) called BlogPress which had some really nice reviews. (Using it right now, with a little help from my java programming husband).
 
 So Day 1 assignment is to “Write your goals for the school year. Be as specific or abstract as you’d like to be.” This is quite an overwhelming task honestly, there are often so many of them. So after some thought I came up with three and here they are:
 
 1. I am mentoring a teaching fellow in my department this year and so one of my goals this year is to be a good mentor. I know that’s pretty abstract but when you have another teacher’s success or failure connected to how well you discuss teaching, mathematics and learning with that person I find the overall goal pretty important. Mentoring someone in PBL is even trickier if it’s their first time teaching and they haven’t actually seen it in action yet. From doing this in the past, I know I also have to find ways to allow young teachers to express their hesitation and doubts with this method of teaching, so being aware of the discussion and keeping the dialogue open will parts of being a good mentor.
 
 2. My second goal is to work on assessing student learning through listening. One of the biggest issues I am grappling with in the classroom and have thought about a great deal in PBL, is how well students can learn from each other by listening to discussion. In fact, I know that one of the biggest arguments that “doubters” have with PBL is that if students are not just told what the important facts are and given clear instruction (what to learn when) learning can’t happen. I want to find ways in which to assess how well students are learning through dialogue. This was inspired when I heard a talk a year or so ago by Karl Kosko (Kent State University) about a study he did related to student listening and their learning. If I remember correctly there was a direct relationship between how well a student could articulate their ideas during a conversation and how well they listened. (So talking and listening are connected.)
 
 3. My third goal is to think about the connections between PBL and grit or self-efficacy. I gave a lot of thought this summer to the differences between grit and self-efficacy and I think one of the best differences I found was tweeted by a guy named Duane Sharrock (@DuaneSharrock) when he responded to request for any distinctions that people had in a tweet I put out there. He said:
 


So in my mind it seems like Self-Efficacy has more to do with confidence and self-attribution of skills and Grit might have more to do with persistence and determination. I am actually interested in both with respect to what PBL fosters in students. To that end, I am going to do a lot of reading and research to see what’s out there and would love to hear from any readers if you have thoughts or experiences with this.
 
 There are my three main goals for the year. My classes start on Friday, but tomorrow they all arrive – wish me luck! Good luck to all of you out there!

What does “making students metacognitive” mean? – answering “why should someone learn?” in Math

So I recently tweeted a nice article that I read that discussed “12 Questions to Help Students See Themselves as Thinkers” in the classroom (not specifically the math classroom

 

and appropriately, Anna Blinstein tweeted in response:

 

So I thought I needed to respond in a post that spoke to this question. First of all, I should state the caveat that even when I am in a more “standard” classroom (i.e. not a PBL classroom) – which happened to me last year – I try as much as possible to keep my pedagogy consistent with my values of PBL which include

1) valuing student voice
2) connecting the curriculum
3) dissolving the authoritative hierarchy of the classroom
4) creating ownership of the material for students

I find that helping students to be metacognitive helps with all of this. An important aside her is also Muller’s definition of 21st century learning* which is much more than that 20th century learning and education that often comes with direct instruction in the mathematics classroom (not always).I think it’s important to note that the more fluid concept of knowledge that is ubiquitous with technology today and is no longer static in textbooks or delivered by teachers.  Students can go find out how to do anything (procedurally) nowadays, but it is the understanding of it that is more important and the true mathematical learning and sense making.

Anyway, I think I would write way too much if I responded to every one of the questions, but how would I use these questions in my direct instruction class that I taught last year?  What I tried to do was introduce a topic with some problems (and then we would do some practice with problems from the textbook so I could keep up with where my colleague was in the material).  Well, this course was Algebra II, which often referred to prior knowledge that always reminded students of something they had studied before.  I let them use computers to look things up on the internet and use the technology at hand, GeoGebra, Graphing Calculators, each other to ask questions about the functions we were studying.  They could look up topics like domain, range, asymptotes (why would there be an asymptote on a rational function)…but then the bigger questions like “what am I curious about?” had more to do with how did those asymptotes occur, what made vertical vs. horizontal asymptotes and then I would have them do journal entries about them (see my blogposts on metacognitive journaling – journaling and resilience, using journal writing, page on metacognitive journaling).

The more “big picture” questions like “Why learn?” and “What does one *do* with knowledge?” I find easier to deal with because the students ask those.  I think that all teachers find their own ways to deal with them, but I enjoy doing is asking students about a tough question they are dealing with in their life – I use the example of whether or not I should continue working when I had my two kids.  Was keeping my job worth it financially over the cost of daycare? and of course I had to weight my emotional state when I wasn’t working – this is why I enjoy learning and what I do with my knowledge.  When kids see that there’s more to do with functions than just points on a grid, it becomes so much clearer for them – but you know that!

What I really like about Dr. Muller’s list is that he lays out some nice deliberate ways in which we as math teachers can get students to think more clearly and reflectively about mathematics as a purposeful process as opposed to a just procedures that they can learn by just watching a Kahn Academy video.

 

*”Learning – here defined as the overall effect of incrementally acquiring, synthesizing, and applying information – changes beliefs. Awareness leads to thoughts, thoughts lead to emotions, and emotions lead to behavior. Learning, therefore, results in both personal and social change through self-knowledge and healthy interdependence.” Muller http://tutoringtoexcellence.blogspot.com/2014/08/helping-students-see-themselves-as.html

Six of one, half a dozen of the other…I think not

2 Comments

(Sorry, this is a long one! and caveat: I am not claiming that Wikipedia is the be all and end of definitions!)

So according to Wikipedia, PBL means two things (well, three if you count Premier Basketball League, but that’s neither here nor there). If you look up PBL on Wikipedia, the first hit is, in fact, Problem-Based Learning. Why, you may ask? I believe that this is because Problem-Based Learning has been around in various forms longer than Project-Based Learning, but the term itself was coined in the 1960s by Howard Barrows at McMaster University in Ontario, Canada ( http://en.m.wikipedia.org/wiki/Problem-based_learning). You can read more about Barrows’ specific definition of Problem-Based Learning at this site and in my tab at the top of my website that says “Problem-Based Learning.” However, what I feel is one of the biggest parts of Barrows’ definition is the fact that “the problem is a vehicle for the development of problem solving skills” – that is it, that it is the problem – hopefully well developed and set in a context that is interesting, challenging and meaningful to students – through which the students will development and learn the problem solving skills.

Wikipedia names Project-Based Learning (http://en.m.wikipedia.org/wiki/Project-Based Learning) almost the same thing, however, they connect it more to Greeno’s theory of situated learning – “learning by doing” and “teaching by engaging students in investigation.” However, all of these theorists ideas range from about 1991-2006, so it would seem that a PBL by any other name…is not really the same?

One of the most important distinctions in Project-Based Learning (which I will write as PjBL, because you know, it came 2nd, for the record) is the authenticity of the task that is motivated by a larger “driving question” – students learn by creating a project and investigating what they need to do in order to organize or structure their presentation for the project.

So what does this mean in mathematics? A few weeks ago, there was quite a discussion going down on Twitter about what constituted Problem-Based Learning.

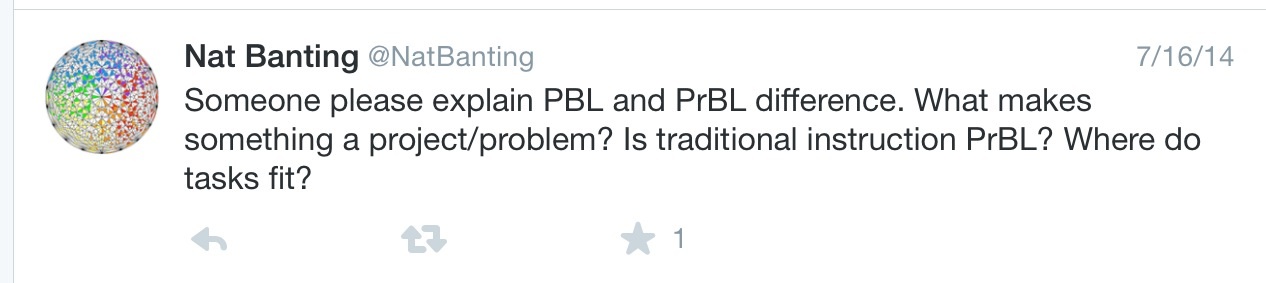
image

image

image

Dan Meyer seemed to be criticizing Problem-Based Learning saying that it was discussed by others as “too much curriculum and too little time for PrBL” and he says that he saw “a lot of fluff in PrBL” – to which I would say, there’s much more to Problem-Based Learning than just doing problems, Mr. Meyer. Nat Banting also asked for a clarification of what the difference was between a project and a problem in math education.

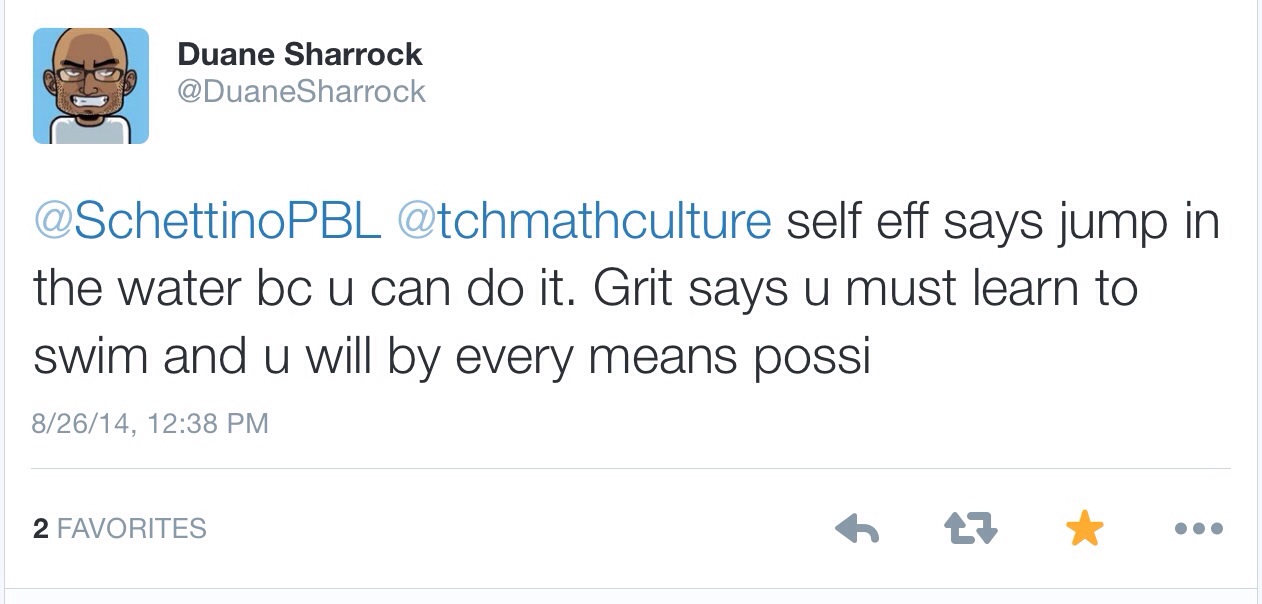
In response to this discussion and Mr. Banting’s question, I posted an image of a table I created listing differences that I saw between project- and problem-based learning in mathematics education and had hoped for some feedback.

image

Then I thought that maybe my description on the image of the differences wasn’t clear enough, so I thought I’d try one more time to make the distinction between the authenticity clear.

If we revisit the idea that Problem-Based Learning has at its core, problems as the vehicle for learning and constructing knowledge, I think this is at the heart of the difference of the learning/teaching experience. When I look at purposefully scaffolded and written curriculum for problem-based learning, yes there are outcomes that need to be met, there are topics that are discussed that are set by the teacher (or curriculum writer). Mathematics has within it many very interesting abstract concepts that are worthwhile to teach even though the “real-life” applications don’t have much context for students (will a student appreciate the logic and problem solving skills that are learned in factoring a polynomial, for example, or do they just accept and take it as a skill they need, or use technology and not use that part of their brain – who knows?) The point I’m trying to make is that in problem-based learning the problems would lead students to figuring out (through discussion and with prior knowledge and experience) the skills needed to create a process of factoring and perhaps “unfactoring” an algebraic expression and hopefully what that expression might represent. This is what’s known as “preauthentication” – when the curriculum writers or teachers try to come up with some kind of experience for the students that simulates the mathematicians authentic experience or “ah-ha” moment of understanding or realization. Then there are other problems that allow the students to dig deeper and apply those ideas to other areas of mathematics, and yes, real-life problems too.

In Project-Based Learning, “emergent authenticity” allows the mathematics to emerge from the ideas of the project (or driving question at hand) which is up to the students to then find out what they need to know. This is where Project-Based Learning can fall short in the area of secondary mathematics – in a world of standards. Where does the learning take place and how does it happen? Once students understand a concept, having gone through rather traditional instruction and some type of formative assessment, the project can then be given. Yes, Mr. Meyer, I believe that there is a hard balance to make there between traditional instruction and when to do the projects – quite a dilemma of time (although schools do it with very nice interdisciplinary time schedules).

However, I do believe that in problem-based learning the rigor, content, problem-solving and all the other “4C’s” skills that project-based learning also promote end up happening in the discussion and presentation of problem ideas and solutions. So I would have to argue with those who say “it doesn’t matter what you call it” and “they’re all the same thing” because the learning process in mathematics is so very different in these two methods. Hopefully, I can shed some light on the differences between PBL and what I hope will be called PjBL soon!

Keeping the Dice Rolling: Questioning in PBL

Returning from a week-long conference is always invigorating for me – not for the reasons that many people think.  I do appreciate the great feedback I get from my “teacher-students” that I interact with during the week who are so extremely eager to learn about PBL – this truly invigorates me and allows me to do so much work over the summer myself.  However, what I always look forward to is how much I personally learn from the interactions with my students that week.  At this point, PBL is so popular in its use in mathematics classrooms across the country, although people see me as an expert in the field, I gain so much from the questions and process of those who are learning that it is so useful for me to move through that process with them all the time.  I believe this is why they call it “professional development”!  So I just wanted to give a HUGE shout-out of thanks to everyone who took my workshops, came to my Cwic sessions, had conversations with me or interacted in some way – it might have been one of the best professional weeks I’ve ever had!

Since that week in New Hampshire, I’ve done a lot of reading, editing of my own materials, and catching up with my own work.  I recently read a blogpost on edutopia entitled “The Importance of Asking Questions to Promote Higher-Order Competencies” which stood out to me as something that we talked a great deal about in my own PBL classes, although this blogpost was not specifically about PBL or math at all.  It was written by a professor at Rutgers University in the Psychology Department, Maurice Elias, who is part of the Rutgers Social-Emotional Learning Lab, and made me wonder if he had done any work with Cindy Hmelo-Silver, who is also at Rutgers and does work with PBL in Psychology.  The concept of asking questions is something that we discuss and practice in my workshops because Hmelo-Silver says that it is a characteristic of an experienced PBL teacher to ask probing questions that are metacognitive and at a higher-order level.  Interestingly, the four areas that Elias discuss are often not linked to higher-order thinking (for example, yes/no questions) so I thought I might take his “Goldilocks” example and try it through the lens of math PBL.  Elias’ four questioning techniques are 1)Suggest 2) Ask a Closed Question 3)Ask an open question and 4)The Two Question Rule.

The idea of “suggestion” is one that I always tried to stay away from since student voice and experience is first and foremost in my mind as a pillar of the PBL pedagogy.  Allowing students to make first attempts at making those connections on their own I believe takes precedence over critical thinking skills of choosing from alternatives.  However, that concept of making a choice between alternatives is important as well and might be a very good skill to have them practice every now and then deliberately.  I think I will begin to try this in class.  The next time when it seems like no one has an idea or when the student at the board is going in the wrong direction, I may decide to say something like “Should Joe go with the method of completing the square or factoring here?”

The second idea of asking the closed question (yes or no) is also one that I have always tried to stay away from.  In my experience it’s kind of a conversation staller, but the way it’s explained by Elias in his blogpost is actually a very interesting twist on the closed question.  It takes a yes or no question but embeds an opinion in it, so almost forces a justification of the closed question with the yes or no.  It makes the teacher find a way for the student to continue (well, the teacher must make sure the student follows up).  So for example, if the teacher asks asks, “Do you think the quadrilateral is a rhombus?” it might seem very obvious that a student could just say yes or no and the conversation could just end there.  Everything I’ve read about closed questions say that you should not phrase the question that way but be sure that the question has within it some interest in the student’s opinion. “Why do you think it’s a good idea to argue that this quadrilateral is a rhombus?” (Which is a closed question in disguise but opens up the conversation).

Then there’s the Open-Ended Question (or what Bingham calls a True Question) which I have written about before.  I talk about this in my workshops as well and real open-ended questions are questions that the teacher doesn’t really know the answer to.  I love Bingham’s analogy of trying to predict with your students what the sum of two dice will be (the answer)  but trying to keep the dice rolling for as long as possible without knowing the answer.

Dice Metaphor

What’s an example of this type of question in mathematics?  This is a tough one because as we know so well, there are definitely right and wrong answers in mathematics.  However, we can ask questions like “Why did you chose that method?” and “What do you think of Sara’s argument? Do you agree with her?” These types of questions can make mathematics teachers very uncomfortable but we can keep the box wiggling for great deal longer than we could before with these questions and they allow us to work towards the CCSS Mathematics Practice Standards of persevering and critiquing other students’ work.

Elias’ Two Question Rule isn’t just as simple as asking a follow-up question, but makes the assumption that students want to see if when you ask a question the first time, you really wanted to know what they wanted to say.  For example, in most mathematics classrooms, students are accustomed to the I-R-E form of dialogue which is short for Initiation-Response-Evaluation (Teacher-Student-Teacher) where the teacher generally knows that answer that they want for the question they have asked (kids know this, they’re not dumb).  So when the same old kids do the response part of this, instead of just doing the evaluation part, why not blindside them and actually rephrase the question and ask it again in a different way, or ask one kid themselves individually in order for them to know that you really want to hear from them?  I think that’s what Elias is talking about.  (or even better don’t use IRE, break that darn habit, I know I’m still trying to!)

We had some great fun during my workshops role modeling and just trying out different ways of questioning the mock student who was at the board – it’s hard to break old habits.  But the more we are aware of what we are trying to do and do it deliberately, the more important it becomes and bigger agents of change we can be as well. If you have any thoughts on these questioning techniques in math PBL classroom – please let me know

Hmelo-Silver & Barrows (2006). Goals and strategies of a PBL Facilitator. Interdisciplinary Journal of Problem-Based Learning , 1(1), 21-39

Looking for the Teacher of Grit

I’m in the middle of working on organizing my courses for the Exeter conference in about a week and something I’m really struggling with is trying to articulate to teachers how they can impart to their students this idea of grit in the PBL classroom.  So I started doing a little research online (besides looking through all of the books I have read on the subject).  I took Angela Duckworth’s Grit Test at her lab’s website (got a 3.63 grit score- grittier than 60% of other U.S. citizen’s my age…hmmm).  Then I started reading some blog posts of other PBL teachers and writers like here on the MAA’s blog which is trying to encourage math students to tinker with problems or here which is more of an all-purpose index of resources to teaching grit. There was this wonderful video of a teacher in NH who created a neat grit curriculum for her 5th grade class (with Angela Duckworth too)

John Larmer of the Buck Institute wrote a really nice blog entry on how project-based learning fosters grit in students. I even found a nice video of Po Bronson, author of Nurture Shock (the book about how parents have failed kids because we don’t let them fail).  This is a short video of how Mr. Bronson believes we should be allowing kids to fail these days.

He says (in so many words) that if kids grow up without learning how to fail, they will become risk-averse.  This is what I am finding in my classroom at times.  The risk-averse kid combined with the fixed mindset kid, combined with the “I-have-to-get-into-college-and-make-my-parents-happy” kid makes the PBL classroom very difficult when you are trying to get them to take risks and be creative.  Add that to the classroom culture that they have been used to for the first 9 years of their education in the U.S. and sadly, it makes for a tough place to foster the teaching of grit.

In fact, on my most recent course evaluations I asked students what they found most challenging about the class and the two pieces that tied for first place were journal writing and

“having to be vulnerable and make mistakes in front of my peers.”

I so want to change that and I always thought that I created a classroom atmosphere where students were comfortable.  I did all of these things that the professionals are suggesting on these websites:

1. modeling risk-taking and making mistakes myself
2. talking about growth mindset regularly
3. ask them to write about positive experiences when they are proud of themselves
4. using class contribution feedback forms (self-report and analysis of class contribution sheets)
5. using strategies where students think of a wrong way before we talk about the correct solution method together.

But somehow, even at the end of the year, their fear of being wrong in front of each other (and me, some commented) is still predominantly what they say challenged them.  So I would say to Po Bronson, where is the teacher of Grit?  What is the secret?  How do I make it so?  Is there a time when it’s too late for some kids?  Most of what I’ve seen on the internet is teaching grit to elementary school children – does the fact that I am teaching high school kids make it any harder?

I finally found this great Prezi created by a teacher named Kristen Goulet which, I know, is geared towards elementary school kids, but I think I could find a way to direct it towards older students.  The idea of having them ask themselves whether their self-talk is “because of me” or “because of other” and whether it is “permanent (i.e. fixed mindset)” or “temporary (i.e. growth mindset)” definitely would help them realize how much of the way the deal with adversity is flexible.  It also helps with seeing how to have a more realistic and optimistic view of a certain situation (and is kind of hard to argue with).

So, I’m still in search for the best practices to teach grit (and apparently so is Angela Duckworth – she admits this in her TED talk), but now I know that it is way more complex than just following a certain number of steps – it has so much more to do with a student’s socio-emotional state of mind. Vicki Zakrzewski’s article “What’s wrong with Grit?” is probably the closest I got to agreeing with someone’s assessment of grit and how to teach it.  I know that I am really good at letting kids know what is important to me and doing that modeling that is important as well.  Undoing what has happened to them before they got to me is a tall order, but I’m not going to stop trying.

Finding Inspiration In All Sorts of Places

“Kids will never understand fully if you just tell them the answer.  They have to break it down and understand it, take it piece by piece ‘cause if you get it straight on you’ll never know what happened. Like if you’re building something you’ll never understand how it’s built, you can never build it again because you don’t know what to do.”

You might think this quote comes from an experienced teacher who has worked with many students over years of seeing how they learn best.  Someone who has found that over time best practices have shown that individuals must spend time with material and grapple with their own understanding in order to learn for understanding.  However, this weekend I heard a fifth grade student named Jessica say this very quote in a video.  Words of wisdom from this young student who has experienced learning in a way that has been very meaningful to her.  Another teacher puts it this way:

“We’re asking students to do things that, at first, may be a little beyond them. But because of the way we present it, they find that they can do it. They’re not finding out how to do it by listening to the teacher explain.  They’re experiencing themselves as people who are capable of learning increasingly difficult skills. Confidence comes from knowing that “I can do it!” – Ted Swartz, Ph.D.

This may be the most controversial part of my definition of PBL.  The concept that not only the students are learning through their own inquiry and curiosity, but that they are asked to apply their own prior knowledge and to do so at an increasingly difficult rate of skills.  That they are asked to challenge themselves again and again.  Another big difference is the way that students experience themselves.  Swartz states that students experience themselves as learners who are capable of so much more than just listening to a teacher and doing what someone external to themselves tells them to do.  They are capable of their own direction in learning and of learning increasingly difficult tasks and managing those.

Also, students in these types of classrooms are concurrently practicing and learning new skills.  This is very different from the way we all learned as children and adolescents and it also goes against the culture of the math classroom in most of the U.S. today so we must set new norms and explain this to parents.  But it is something that is very rewarding.

We just had our Parents’ Weekend at my school and the two new teachers who were working on our pilot PBL shared with me stories of parents who had had negative feelings towards the curriculum at the beginning of the year.  I was nervous about how they were responding now, at the end of the school year.  However, to my surprise, my colleagues shared with me stories of how proud of these parents were of their students presenting in front of the class and articulating mathematical concepts to their classmates very well.  Are these straight A students now?  Not at all, but they are proud of their work, engaged in the discussion and enjoying math class.  These are great strides for these students.  And at the end of year where we worked very hard, this was truly inspirational.

PBL at NCTM 2014!

One of my major goals in attending the NCTM annual conference this year was to see how widespread PBL had become in terms of mainstream education practices across the US.  I have to say that this year there were quite a few sessions that had PBL in the title or as the central theme and I was excited to see that!  Here were some of the workshops:

Problem-Based Learning (PBL) Is More Than Solving Problems – in this session the speakers were giving just a beginner’s view of what PBL is and can be in the classroom.

Change the Classroom, Not the Students – Attaining Equity Using PBL (OK, this one was mine)

Bring Back Problem-Based Learning into Methods Courses! – in this session the speaker makes an argument for using PBL methods in courses for teacher candidates and spoke about the positive experiences of preservice teachers with PBL.

Amplify the Mathematical Practices -this session focused on middle school PBL practices and how they stressed the CCSS MP standards.  This was sponsored by Amplify’s Math projects.

Making Mathematics Culturally Relevant to Students Using Problem-Based Learning – in this session, the speakers gave an example of culturally relevant pedagogy striving for equity in the classroom.  Again arguing that PBL allows for furthering equity in the practice of PBL.

Setting the Scene: Designing Your Problem-Based Classroom – in this session, the great Geoff Krall (emergentmath.com) gave a great talk summarizing a lot of his methods relating to PBL and his protocols in getting students to work through problems in their learning.

The Hidden Message: Micromessaging and Mathematics – I wanted to attend this session so badly, but I had to leave early on Saturday morning.  This session has so much to do with my own research relating to how we talk to each other in mathematics classrooms and how PBL can allow for better communication without the micromessages.  (Tujuana if you read this – get in touch with me!)

Promoting Equity through Teaching for a Growth Mindset (Jo Boaler) – in this Session Prof. Boaler reported on her work in math education with Carol Dweck’s Mindset research.  You should check out her new website youcubed.org if you are interested in all the resources that she has shared freely.

And that was just to name a few!  So much wonderful information out there to learn and share.  The variety and number of sessions that connected to the pedagogy, content or philosophy of PBL was overwhelming and honestly very invigorating for me as someone who has taught with PBL for over 20 years.  Seeing the interest and enthusiasm for this type of classroom practice has given me renewed energy to get me through the rest of the year!

What I learned over my NCTM break!: Part 1

Wow!  What an amazing three days I spent at the NCTM annual conference in New Orleans!  I can’t believe how much I learned (which actually never amazes me and always humbles me – one of the many reasons I love going to these conferences.)  I also hate leaving and knowing that I missed at least 20 sessions that conflicted with ones that I did go to, so now I’m catching up and trying to email the speakers that I didn’t quite get to see or get in contact with while there.

One of my major a-ha moments was in Gail Burrill’s session on logarithms.  You’d think that after 25 years of teaching that you’d understand how much you understand about logs right? Oh, no!  So she had us all have a very large number and we were doing an exercise where we had to put a post it note with that number (mine was 72, 753) on a scale of powers of 10 {10, 10^2, 10^3, 10^4, 10^5…}, her argument being that one of the main reasons to teach logs is to have a different scale for very large numbers.  So after all of these teachers did this, we analyzed where all of our numbers were on the scale – particularly between these numbers.  Since my number should’ve been between 10^4 and 10^5, I knew I put it in the right place – but oh no, I had it in the wrong place relative to the middle.  She asked us to calculate the middle of those two – 10^4.5 which was 31,622 and yes, I admit that’s very close to where I put my post-it.  I could blame the person who put their’s up first which said 75,289 and I just put mine by there’s but I won’t.  I just didn’t really think.  But I know this was a light bulb moment for many of the teachers in the room.  Students don’t really understand how a logarithm is an exponent in the first place and we were doing this exercise without even using the word “logarithm.”

Then we went down to the section below that was between 10^3 and 10^4 and checked some of those numbers.  They were very off too and Gail asked us what number we expected to be in the middle.  At this point, some of us pulled out our calculator (yes, I admit, I did) but some of the smartees in the room just said “3,162” and I finally got it.  By just dividing by 10 and looking at the scale in this nonlinear way, students would be able to make the connection between the algebraic properties of exponents and what a logarithm was.  I thought this was an amazing way to introduce logs.  Has anyone done this before?  Thanks so much Gail!!  I think I’m going to write a problem for my curriculum about this, it’s such an insightful experience.

More reflections to come – just can’t do it all at once – catching up on school work!