Author: Carmel

NCTM 2015 – Reflections

I know I’m a little late but I did want to post my own handouts and talk a little bit about my experiences at NCTM Boston this year.  I want to thank all of the great speakers  that I saw including Robert Kaplinsky, Ron Lancaster, Maria Hernandez, Dan Teague, The Young People’s Project (Bob Moses’ Group), Deborah Ball, Elham Kazemi and of course the inspiring Jo Boaler.  One of the things I thought was great about Jo Boaler’s talk on Thursday night was that even though I had heard a great deal of what she had said before, there was a different tone in the room.  I’ve been a fan of Jo’s since I first read her research in 2001 when I started my doctoral work on girls’ attitudes towards mathematics learning.  What I felt that was different that night was that she was no longer trying to convince people of anything.  There was a different message and that was “join the revolution” and the audience seemed to be on board and excited.  It made me feel very energized and empowered that a huge ballroom full of mathematics educators had bought into her ideas and were enthusiastic to make change happen.

Some of the best times I had were spent just connecting and reconnecting with people – some who I met for the first time (MTBoS folks and other Twitter folks I met F2F which was really nice) and others who were old friends who mean a great deal to me.  I forget how much the mathematical community of professionals enriches my life and makes me proud to do what I do.  Thanks to everyone who reached out to find me and say hi – or tell me a story, talk to me about what they are doing or ask a question about what I am doing.  You are all inspiring to me.

I left the conference with exciting ideas about teacher observation for PD, how teachers can share problems with each other better on the internet (awesome resources at Robert Kaplinsky’s problem-based lesson site), great ideas about agent-based models to add to courses, and ways in which teachers can talk to people about the Common Core and gain respect about the difficult work we do in teaching.  Overall, I felt like it was an amazing time.

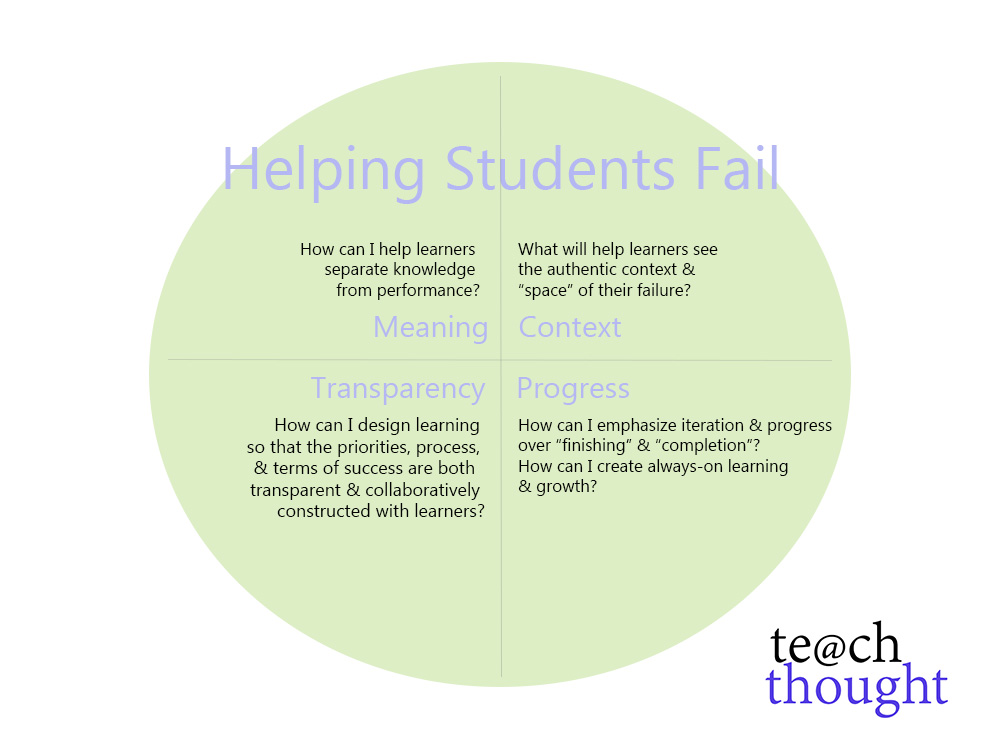
I want to thank everyone that came to my session.  Although I had an unfortunate technological snafu and was unable to do an exercise I had planned where we were going to analyze a segment of discourse from my classroom using the framework of the MP standards (which would’ve been great), I felt that at least the resources that I shared were worthwhile for the people that came.  Here is a link to the powerpoint presentation and the handouts I gave.

 

Handout 1 NCTM 2015 Schettino

Weekly Learning Reflection Sheet

Handout 2 Schettino

I’ll just put in one more plug for our PBL Summit from July 16-19 this summer – we still have a few more spots and would love to have anyone interested in attending!

Spring has Sprung – and so has the French Garden!

So the spring term means two things for my Honors Geometry kids – the technology inquiry project and looking at the French Garden Problem.  So for those of you who are not familiar with both of those I’ll try to quickly fill you in while I talk about how they just happen to so coolly (is that an adverb?  if not I just made it up) overlapped this week.

My Spring Term Technology Inquiry Project is something I came up with three years ago when I really wanted a way to push my honors geometry students into thinking originally while at the same time assessing their knowledge of using technology.  I did a presentation last year at the Anja S. Greer Conference on Math, Science and Technology and the audience loved it.  Basically, I give students an inquiry question (one that I attribute to my good friend Tom Reardon) that they have to work on with technology and then they have to come up with their own inquiry question (which is, of course, the fun part) and explore that with technology and/or any other methods they wish.  I have received some pretty awesome projects in the past two years and I don’t think I am going to be disappointed this year either.

The French Gardener Problem is famously used in my PBL courses at the MST Conference as well.  Everyone who has taken my course knows the fun and interesting conversations we have had about the many ways to solve it and the extensions that have been created by many of my friends – an ongoing conversation exists somewhere in the Blogosphere about the numerous solutions – In fact Tom sent me a link just last fall to a more technological solution at Chris Harrow’s blog. (We’re such geeks).  Great math people like Phillip Mallinson and Ron Lancaster have also been drawn in by the attractive guile of the The French Gardener Problem.  In this problem, the main question is what fraction of the area of the whole square is the octagon that is formed inside (what is the patio for the garden)?

So the other night, after we had worked on this question in class for a couple of days and the students had meet with me in order for me to approve their original inquiry question, a student stops by to discuss his question.  John starts off with, “I can’t think of anything really. What I had wanted to do, someone else already claimed.” (I’m not letting them do a question that someone else has already decided to look into.  So John sits in my study and thinks for a while. I told him that this part of the project was supposed to be the fun part.  I gave him some thoughts about extending some problems that he liked.  He said he had liked the French Garden Problem and thought it was really cool.  So I went back to some of my work and he started playing with GeoGebra.  Before I knew it he starts murmuring to himself, “Cool, cool….Cool! It’s an octagon too!”  I’m thinking to myself, what has he done now?  I go over to his computer and he’s created this diagram:

John's Original Inquiry Question
John’s Original Inquiry Question

I’m asking him, “What did you do? How did you get that?”  He says that he just started playing with the square and doing different things to it and ended up reflecting equilateral triangles into the square instead of connecting the vertices with the midpoints as in the original French Garden Problem.  Then he started seeing how much of the area this octagon was and it ended up that it was……you don’t think I’m going to tell you, do you?

Anyway, it just made my night, to see the difference in John when he came by and the by the time he left.  He was elated – like he had discovered the Pythagorean Theorem or something.  I just love this project and I would encourage anyone else to do the same thing.  Leave a comment if you end up doing it because I love to hear about any improvements I could make.

Why Can’t We All Just Get Along?: Some Inquiry Math Classes are not Content-less

Maybe it’s just how I am, or maybe I’m just always worried about what people are going to say about me, but I am hesitant to criticize other teachers publicly in the blogosphere. I’ve always felt this camaraderie with others once I’ve learned they were a teacher even if we are very different from each other – different disciplines, different pedagogical styles, different countries – there are still fundamental commonalities that even public and private school teachers have.

I just finished reading a KQED blogpost entitled “Do You Have the Personality to be an Inquiry-Based Teacher?” that sort of summarizes the theoretical qualities that the author feels a teacher who would teach with IBL would need to exhibit in order to successfully run a classroom. It’s kind of interesting – I’m not sure I agree with it, but respect the author for putting his ideas out there. I’ve been an inquiry/problem-based teacher for almost 20 years and I don’t think I exhibit all of the qualities listed, so I’m not sure it’s quite true.

Anyway, that’s not the point – at the end of the blogpost there are about 11 comments from people who are educators and many of them are quite negative and even degrading to the author:

“I earned a Ph.D. in Educational Psychology, but phrases like this one still baffle me: “…the divide between a transmission model and an inquiry model…” ”

“First, we need to make sure that we have at least a rudimentary understanding of the language in which we will be teaching. Second, we need to make sure we can write.”

“That is what’s wrong with you teachers.You want to do it your way.”

“Some of us have been doing this for decades, where were you?”

Whoa, Whoa, Whoa…cowboys…hold your horses. This guy is just writing an essay about something he believes in. What kind of role model are we being for our students if this is how we are reacting to something we don’t agree with? What happened to civil communication? I totally agree that people are allowed to comment and voice their opinions on someone else’s opinion, but there has to be a way to do it with respect and decency.

So I am going to try to model what I would like to see as a response to something I actually do disagree with. Here is a blogpost by a very respectable Professor in Canada, who I have to be totally honest, I do not know at all. I tried to learn as much as possible about him before writing a response to his blogpost in order not to make any assumptions about him (and not make a fool of myself in doing so), so I may be wrong about some of this information because I garnered it from different websites. It seems he is a research mathematician who is currently studying to get a teaching degree, but who lectures for mathematics courses at the college level. I cannot ascertain if he has any experience teaching at lower levels (like elementary or secondary). From his blogpost it does seem like he takes pride in the amount of background research he does, which again is very respectable and I appreciate in bloggers. He seems to care a lot about student learning and from his opinions on his blog he seems to lean towards being a behaviorist and cognitive theorist in terms of learning theories.

His latest blogpost is titled “The Content-less Curriculum” and it is a critique of the movement towards 21st Century skills being a part of the mathematics classroom. It does sound like Prof. Penfound is implying that with the inclusion of “soft skills” of collaboration, critiquing others work, problem solving,communication, etc. (i.e. the MPS for the CCSS) there must be a loss of mathematical content. In fact, he says that

“there must be a trade-off for the inclusion of “soft skills” activities into an already packed curriculum. So what gets removed from the curriculum then? Content knowledge.”

I would respectfully, but wholeheartedly disagree with this. By teaching with the PBL curriculum that I use, I have all of the college prep geometry curriculum I desire and I also concurrently am assessing and teaching the skills of problem solving and the so-called “soft skills” that he is implying are an add-on. I still give quick quizzes to make sure that students are up on their basic skills that are so important for basic problem solving (or else they wouldn’t be able to do the open-ended problems they are given).  The mathematics that students leave my courses having experienced is rich and leaves an impression on the way they think.

Making blanket statements about teachers implying that we all make choices that are not based in research or good practice is just not true. I actually invite you Prof. Penfound to come visit my classes and see my IBL/PBL classes in practice and let me know what you think of your opinions of the rigor of the mathematics that is discussed. Although we are most likely at different ends of the spectrum in terms of learning theories, I do believe that students have different needs and try to work with kids’ learning needs individually. However, I do believe as @danieldmccabe does that there are going to be new outcomes required of our ever-growing diverse body of graduates in the near future (or even present). I also have to say that I have thought rather thoroughly about the implementation of a teaching program which includes “soft skills” and even wrote a dissertation on it.

It is possible to balance content and practice skills and it is what I and many other classroom practitioners strive for. I do not deny that there are some practitioners out there that are confused about what problem-based and project-based learning outcomes should be especially with regard to secondary mathematics, but that is a subject for another blogpost.  The balance between content and practice skills we should strive for does not mean that one is more important or less important and in fact they both need to be assessed with the ultimate goal being to create independent problem solvers. From my experience this does not necessarily happen in a classroom where the educator does not take into consideration the so-called “soft skills.” But that statement is, of course, based on my 25 years of anecdotal classroom experience.

 

Succeeding at Helping Students to Fail?? Part 1: Meaning

Apologies faithful readers – those of you who know me well, know that I have been dealing with a great deal of personal issues and preparing for the summer PBL Math Teaching Summit, so I have taken a small hiatus from blogging for a while.  However, with that under control for now, I turn to reflecting on something that happened in class the other day and its relation to a great article I retweeted that was on TeachThought’s website the other day entitled Helping Students Fail.  I have been giving a lot of thought this year to the idea of Grit and Problem-Based Learning which has intrigued me for a while.  However, this article is one of the few I’ve seen that really speaks to some concrete steps that teachers can take to aid students on the journey of dealing with making mistakes and viewing them in a positive light.

I love the framework that the author gives here:

http://www.teachthought.com/teaching/the-role-of-failure-in-learning-helping-students-fail/
Helping Students Fail: A Framework by Terry Heick

Breaking the struggle into these four aspects of learning is very interesting to me (of course with respect to the PBL Classroom).  It dawned on me while reading this article that this is a continuous and completely ongoing process of learning to fail that happens.  It is so ubiquitous that the teacher and students are probably not even aware of it (or are so aware of it that that’s where the discomfort is emanating from).  It is so ubiquitous that I needed this framework for me to be able to even have it spelled out for me.

1. Meaning: In the PBL classroom, meaning is shaped everyday – the explicit separation between knowledge and performance is spelled out in discussion and the way students are asked to share their attempts at problems.  Jo Boaler might have spelled it out best in her paper desribing the Dance of Agency, where she explained the importance of sharing what she called “partial solutions.”  Using this language is really important to make sure that students don’t feel the need to have a complete solution when they present (because no matter how many times I say it, they still say, “Is it OK if it’s wrong/”)  In their mind, they feel their presentation is a performance.  However, the other day I had an interesting experience while students were presenting.  We were doing this problem in class and I had assigned two girls to present their ideas together:

A triangle has sides measure 9, 12 and 15 (what’s special about this triangle?).  Find the distances to the centroid from all three vertices.

The day before we had done a problem very similar to this with an equilateral triangle of sidelength 6 and the presenter had realized that he could connect this problem to the work we were doing with 30-60-90 triangles.  He then applied the Centroid Theorem which states that the centroid is 2/3 of the way from the vertex along the median.  So when the girls presented, they did this:

FullSizeRender (1)

They realized that the median from A was the hypotenuse of a right triangle and they could find its length with the Pythagorean Theorem. They then used the Centroid Theorem and found 2/3 of it. However, next, they did this:


FullSizeRender (2)It was great that they connected this problem to the previous day’s presentation where all of the distances were the same (I’m always asking them to look for connections). However, when I asked them the question of whether they expected those distances to all be equal, they had to think about that. We put the question out to the class and it started a great discussion about why sometimes they were the same and sometimes they weren’t. I won’t go into the whole solution here since the correct answer is not the point of this blogpost but what happened that evening is.

Later on that night, I received an email from one of the girls who was part of the presenting team. At the end of class, I had noticed that she seemed very quiet and I had asked her if she was confused about something else we were discussing towards the end of the class when the bell rang. She had said no and left class very awkwardly.

This is what she wrote to me:

FullSizeRender
I had been working so hard to make students feel comfortable making mistakes that I wasn’t paying attention to who had made the mistakes and that they were actually comfortable making the mistakes and proud of making those mistakes and wanted credit for making those mistakes! I was dumbfounded. I just couldn’t believe it. My perception of (at least) this student’s ability to be comfortable with being wrong was so different than what her’s was. She was proud that her “mistake was a good one” and not just a “silly error” and I needed to give her the credit she deserved for taking a risk. I learned such a great lesson from this student on this day and I owe her so much (and don’t worry, I told her that in an email response)!

The separation between knowledge and performance has been made clear to at least some of my students and I am going to keep doing what I’m doing in the hope of getting this message to all of them.

Tracking, PBL and Safety in Risk-Taking

I’ve been giving a lot of thought recently to the idea of “tracking” in PBL, mostly at the prodding of the teaching fellow I’m working with this year – which is so awesome, of course.  Having a young teacher give you a fresh outlook on the practices that your school has come to know and accept (even if I don’t love them personally) is always refreshing to me.

I have taught with PBL in three different schools – two that tracked at Algebra II (or third year) point in the four-year curriculum and now one that tracks right from the start.  Anyone who has done Jo Boaler’s “How to Learn Math” course has seen the research about tracking.  So the question that my teaching fellow asked me, is why do we do it.  The answers I had for him were way too cynical for a first year student teacher to hear – “Because it’s easier for the teachers to plan lessons and assessments.” “Because the class will be easier to manage, as well as parents.”, etc.

In fact, I would have to say that in a PBL math classroom the experiences that I had with the heterogeneous groupings ended up being really advantageous for both strong and weak math students.  Here’s a great quote from a weaker student in a heterogeneously grouped math class, who was part of my dissertation research (that I have used before in presentations) when asked what the PBL math classroom was like for her:

“You could, kind of, add in your perspective and it kind of gives this sense like, “Oooh, I helped with this problem.” and then another person comes in and they helped with that problem, and by the end, no one knows who solved the problem.  It was everyone that solved the problem.  LIke, everyone contributed their ideas to this problem and you can look at this problem on the board and you can maybe see only one person’s handwriting, but behind their handwriting is everyone’s ideas.  So yeah, it’s a sense of “our problem” – it’s not just Karen’s problem, it’s not just whoever’s problem, it’s “our problem”.

This shared sense of work, I believe, rubs off on both the strong and weak students and allows for mutual respect more often than not.  Even my teaching fellow shared an anecdote from his class wherein a stronger student had gotten up to take a picture with his iPad of a solution a weaker student had just been in charge of discussing.  The presenter seemed outwardly pleased at this and said ,”He’s taking a picture of what I did? that’s weird.”

This mutual respect then leads to a shared sense of safety in the classroom for taking risks.  Today I read this tweet from MindShift:

I don’t really read that much about coding, but when something talks about risk-taking, I’m right there.  In this article, the student that decided to go to Cambodia and teach coding to teenage orphans makes a really keen observation:

“Everybody was a beginner, and that creates a much more safe environment to make mistakes.”

So interestingly, when the students in a classroom environment have the sense that they are all at the same level, it allows them to accept that everyone will have the same questions and opens up the potential that all will be willing to help.  I don’t think this has to be done with actual tracking though – I think it can happen with deliberate classroom culture moves.

I got more insight into this when asking some students in my Honors Geometry class why they don’t like asking questions in class.

“It seems to not help that much because it shows others how much I don’t know.”
“It only allows others to feel good about themselves instead of make me feel better that my question was answered.”
“If someone else can answer my question then they end up getting a big head about it instead of really helping me understand.”

I was starting to see a trend.  Now, this was not all kids, don’t get me wrong, but it was enough to get me concerned – This reminded me of a great blogpost I read by John Spencer (@edrethink) called The Courage of Creativity in which he write about how much courage it takes to put something creative out there and fail.  In mathematics, many students don’t see it as being creative, so hopefully John won’t mind if I change his quote a little bit (since I am citing him here, I hope this is alright!)

“All of this has me thinking that there’s a certain amount of courage required in [risk-taking in problem solving]. The more we care about the work [and are invested in the learning or what people think of our outcomes], the scarier it is. We walk into a mystery, never knowing how it will turn out. I mention this, because so many of the visuals I see about creativity treat creative work like it’s a prancing walk through dandelions when often it’s more like a shaky scaffold up to a mountain to face a dragon.”

Thanks John!

PBL Summit News!

It’s been an extremely busy fall for me, but with the help of my friend Nils Ahbel, I have finally put together an informational flyer and schedule for the Problem-Based Learning Math Teaching Summit for next summer.  As you begin to look for professional development opportunities for yourself, please consider being a part of this great summit where like-minded math teachers can gather and share ideas.  Currently, we are making this information available and registration and final pricing will be available in January.  If you have any questions regarding the summit, please feel free to contact me.

Check out the PBL Math Summit Flyer 2015 here. For further information see the page on the PBL Summit.

How do we get kids to value others’ ideas in math class?

Some recent common situations:

A very gifted student comes to me (more than once) after class asking why he needs to listen to other students talk about their ideas in class when he already has his own ideas about how to do the problems.  Why do we spend so much time going over problems in class when he finished all the problems and he has to sit there and listen to others ask questions?

A parent asks if their child can study Algebra II over winter break for two weeks and take a placement test in order to “pass out” of the rest of the course and not have to take mathematics.  A college counselor supports this so that they can move forward in their learning and get to Calculus by their senior year.

Tweet from a fellow PBL teacher:


Over the summer, a student wants to move ahead in a math course and they watch video after video on Khan Academy and take a placement test that allows them to move ahead past geometry into an Algebra II course.  Why would they need to spend a year in a geometry course when they have all of the material they need in 5 weeks of watching videos all alone?

It is a very accepted cultural norm in the U.S. that math is an isolated educational experience.  I’m not quite sure where that comes from, but for me, it remains a rather traditionalist and damaging view of mathematical learning.  I would even go so far as to say that it could be blamed for the dichotomous view of mathematics as black or white, right or wrong, fast or slow, etc.  For many students, if they don’t fit that mold of a mathematics learner who can learn math by watching someone do it, sitting nicely and taking notes for 45 minutes while we ‘cover’ section 2.4 today, then they are ‘bad at math.’

Leone Burton once said that the process of learning mathematics is an inherently social enterprise and that coming to know mathematics depends on the active participation in the enterprises so valued and accepted in that community (Burton, 2002).  In other words, if we accept the status quo of the passivity of mathematics learning that is what we will come to believe is valued.   In her research on the work of research mathematicians and their mathematical learning she found that the opposite of the status quo was true.  The collaborative nature of their practice had many benefits that mathematicians could claim including sharing work, learning from one another, appreciating the connections to others’ disciplines and feeling less isolated (Grootenboer & Zevenbergen, 2007).  Collaboration was highly valued.

We are doing students a disservice if we allow them to remain in the status quo of being passive mathematics students or thinking that they do not have to share and/or listen to others.  The CCSS are asking (well, requiring) them to critique others’ work and give feedback on problem solving methods.  They need to be able to say what they think about others’ ideas and construct their own argument.  How are they going to learn how to express their reasoning if they don’t listen to others and attempt to make sense of it?

When working and/or learning in isolation students are not asked to do any of this or even asked to make mathematical sense oftentimes.  They are just asked to regurgitate and show that they can repeat what they have seen.  How do we know they are making any sense if they do not have to respond to anyone or interact with a group?  The importance of the social interaction becomes apparent in this context.

So what I try to explain to students is that mathematics means more to me than just being able to have a concept “transmitted” to them by someone showing them how to do something, but for them to actually do mathematics in a community of practice.  Creating that community takes a lot of work and mutual respect, but it’s something that is definitely worth it and I encourage everyone to keep inspiring me to keep doing it!  Thanks @JASauer.

The First Followers…how do I get them in the PBL classroom?

2 Comments

So I have one class this year that is rather frustrating and pretty tough to handle when it comes to buy-in with what I’m doing in the mathematics classroom.  Perhaps it’s because it’s first period, or perhaps it’s the mix of kids (quiet, shy, cynical?) – but I’m having a hard time inspiring them to speak out about their ideas or even be somewhat active in class.  This has made me wonder if I’m doing anything differently?  What’s the difference between first period and second period?  Why would this class be that much different in student make-up and personality than other challenging classes that I’ve had.

These thoughts made me remember a video I saw at a conference talk this summer and how important the “first followers” are.  This video is basically about a guy the narrator calls the “lone nut” who is dancing at a music festival (maybe you’ve seen it, it’s been around for a while) and how his leading becomes a “movement.”

It’s one of my favorites and so true.  But what I am afraid of is that the “first followers” I had in my first period class are not necessarily “followers” but students who realized they better do what I want or they won’t do well in my class.  This is not the same as “buy-in” to PBL.  This led me to think about what I needed to do in order to create first followers who would truly be inspiring and lead to more followers.  I’m not sure about this, but a couple things I tried:

  • talking about the pedagogy and how it’s different with the students
  • discussing the class contribution rubric with them and having them do a self-evaluation of their contributions to class
  • discussing listening skills when learning
  • Being deliberate about asking questions that are more open-ended (not just procedural)
  • Being less “forgiving” that it’s first period and they are tired – keeping my standards up of what I expect from them.
  • Giving praise when students take risks and learn from mistakes at the board
  • Offering a reward (like a Pez Candy) when a student is wrong but has taken a risk

So far my attempts have not been in vain, but I still don’t feel the “movement” as I do in other classes.  This has been an interesting first month with this group and I think many of them are actually learning, but don’t seem to be enjoying themselves.  I think I just need a couple more “first followers” to allow the others to see that what I am asking of them – although harder and requiring more energy and effort on their part – is actually an important part of their journey of learning.  I would love to hear from anyone who has experienced this and what steps can be taken to increase the followers in a “mob” of the whole class!

Teaching Persistence Takes Time….But How Much Time?

4 Comments

I just read a great story posted on a blog about Malcolm Gladwell’s comments about Alan Schoenfeld’s research on persistence in problem solving in Gladwell’s book Outliers. In this story, a young woman persists for 22 minutes on a problem that had an average persistence time for most students of about two minutes.  Of course we would love to have students be persistent in the face of a problem they couldn’t solve and have some determination and creativity to bat to allow themselves to grapple with the problem (in other words, not just sit there and persist in the feeling of gosh-I-wonder-how-to-do-this).

But at the same time, imagine that you actually have kids who are well-intentioned, pretty smart and actually interested in learning.  Let’s just give them the benefit of the down for a second here – and we’re in a classroom where we have interesting problems that might keep them engaged in the evening with an cool idea with which they must grapple for a while.  I would ask the question, “How persistent do we want them to be?” (and so would they).

Many kids in the PBL classroom wonder this in the beginning of the year and I am asking myself now too.  This student of Schoenfeld’s that persisted for 22 minutes –  is that a good thing?  How long is too long?  When would we want a kid to know to look for resources?  To question their prior knowledge in a different way?  To know to stop and wait to discuss with others the next day?  To try using technology?

So my question would be how do we know when we are teaching persistence as a good  and productive thing or when we are teaching students that their problem solving is just the definition of insanity (repeating the same thing over and over expecting different results?).  My thought is that persistence without a growth mindset (or the belief that you can change your way of thinking and knowing) can be just as dangerous as no persistence at all.

Inspirational colleagues? Wow…

OK, so I’m not really doing the full blog challenge – This weekend was nutso and blogging everyday is really tough – enough with the excuses.  But this question, “Who was or is your most inspirational colleague and why?” just really struck me at my core.  There have been so many, probably for all of us in education, it would be extremely difficult to pinpoint just one who was MOST inspirational.  I continue to be inspired rather regularly by my past professor (now friend) Carol Rodgers (SUNY) who is just one of the most amazing writers, Dewey Scholars and researchers and reflective practice I have ever met.  She is an amazing teacher mentor and has taught me a great deal. Ron Lancaster (OISE – Toronto) continues to show me how to be a true teacher of teachers every time I see him.  Nils Ahbel (Deerfield) and Maria Hernandez (NCSSM) and two of the most passionate mathematics educators I have ever met and every time I speak with them about my practice, I learn something new – period.  If you all ever get a chance to hear any of them speak, I highly recommend it.

I’ve already written about my inspiration and admiration for Rick Parris and the amazing life he led as a an educator, so I won’t go into that again, but I do feel that if I had to name someone who was not only inspiring, a major role model, caring, patient and kind, and truly changed my life, it would have to be Anja Greer.  If there is anyone to whom I have to attribute my work and lifelong love of teaching mathematics with problem-based learning, it would be Anja, mostly because I would not have had the opportunities and the courage to have taken the risks and to work with people who intimidated the heck out of me when I was only 26 years old.  She was a woman at school that had a very male-dominated history and she always spoke up for the students that were underserved and underrepresented.  She gave of herself in every way and gave me a job opportunity in 1996 that changed my life.

In the classroom, she was a teacher, mentor, innovator and amazing administrator.  To watch her handle a room full of very opinionated and argumentative mathematics faculty was amazing – never losing her grace and determination.  She took her time finding the words that she wanted to say and to this day, when I feel that I am pressured to quickly say something I think of her, take a breath, and rethink my words in my head.

The day I met Anja she frankly explained that she had to put a wig on in order to take me to campus because the students hadn’t seen her with her hair so short.  You see, she was battling cancer at the time that she was serving as department chair, implementing a new curriculum and hiring 4 new teachers that year.  The courage she had to “put on that wig” and move through her days for the next few years inspired me so much.  My son was born the year she lost her battle to cancer and she still had the compassion to let me know how happy she was for me that January.

I am so grateful for Anja’s influence on my life and I continue, in her memory, to teach annually at the conference that was named for her.  If I can even remotely come close to influencing another teacher in the way she has for me, I will have just started to repay her.