Author: Carmel

Everything Old is New Again…(or why teaching with PBL is so great)

So I heard that what everyone is saying about the new Star Wars Movie, The Force Awakens, is that “Everything Old is New Again” – go ahead google it, there are at least 5 or 6 blog posts or articles about how “BB-8 is the new R2D2” or “Jakku is the new Tattoine” or whatever.  I actually don’t have a problem with J.J. Abrams reusing old themes, character tropes or storylines because I think that really great stories are timeless and have meaning and lessons that surpass the movie that you are watching.  I still thought it was awesome.

This concept of everything old is new again really hit home to me today in my first period class when I was having the students do a classic problem that I probably first did in 1996 while I was under the tutelage of my own Yoda, Rick Parris (who I think wrote the problem, but if someone reading this knows differently, please let me know).  The problem goes like this:

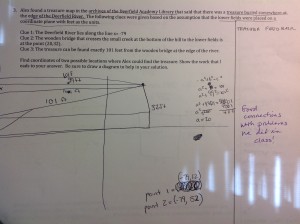
Pat and Chris were out in their rowboat one day and Chris spied a water lily.  Knowing that Pat liked a mathematical challenge, Chris announced that, with the help of the plant, it was possible to calculate the depth of the water under the boat.  When pulled taut, directly over its root, the top of the plant was originally 10 inches above the water surface.  While Pat held the top of the plat, which remained rooted to the lake bottom, Chris gently rowed the boat five feet.  This forced Pat’s hand to the water surface.  Use this information to calculate the depth of the water.

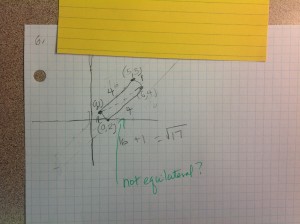
What I usually do is have students get into groups and put them at the board and just let them go at it.  Today was no exception – the first day back from winter break and they were tired and not really into it.  At first they didn’t really know what to draw, how to go about making a diagram but slowly and surely they came up with some good pictures. Some of the common initial errors is not adjusting the units or mislabeling the lengths.  However, one of the toughest things for students to see eventually is that the length of the root is the depth of the water (let’s call it x) plus the ten inches outside of the water’s surface.  Most students end up solving this problem with the Pythagorean Theorem – I’ve been seeing it for almost 20 years done this way.  Although I never tire of the excitement they get in their eyes when they realize that the hypotenuse is x+10 and the leg is x.

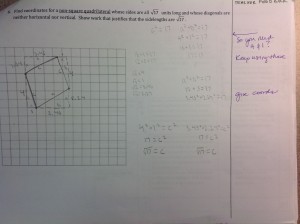
However, since everything old is new again, today I had a student who actually is usually a rather quiet kid in class, not confused, just quiet, but in a group of three students he had put his diagram on a coordinate plane instead of just drawing a diagram like everyone else did.  This intrigued me.  He initially wrote an equation on the board like so:

y= 1/6 (x – 0)+10

and I came over and asked him about it.  He was telling me that he was trying to write the equation of one of the sides of the triangle and then I asked him how that was going to help to find the depth of the water.  He thought about that for a while and looked at his partners. They didn’t seem to have any ideas for him or were actually following why he was writing equations at all.  He immediately said something like, “Wait, I have another idea.” and proceeded to talk to his group about this:

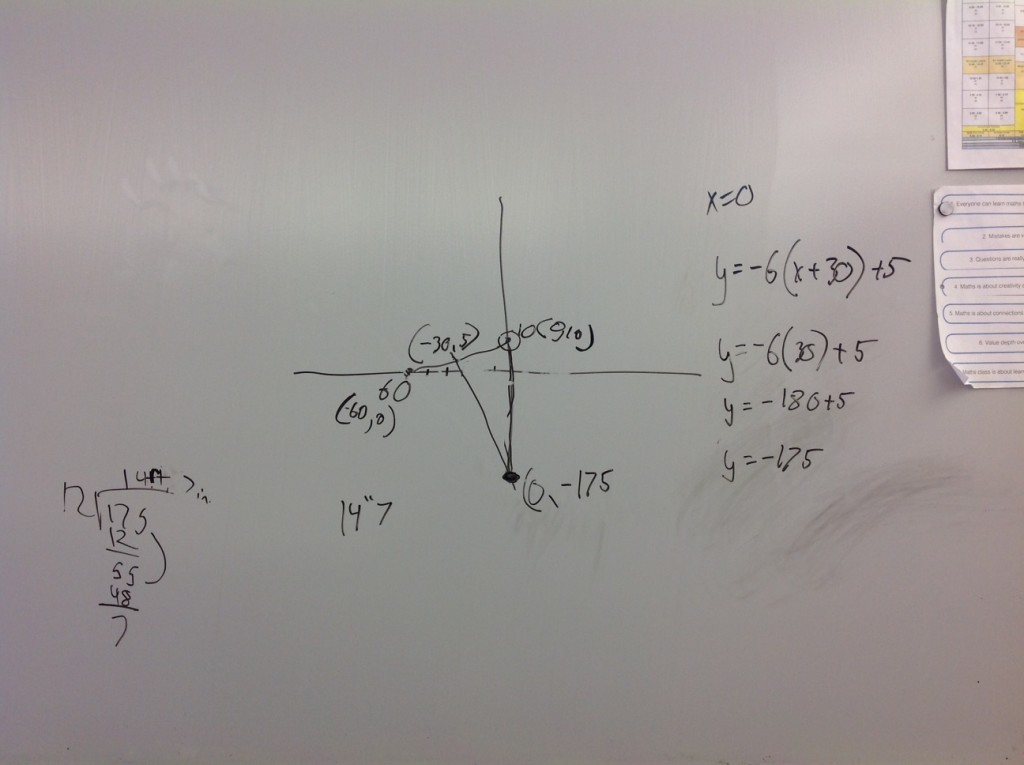
Jacksons solution to Pat and Chris
Jackson’s Solution to the Pat & Chris Problem

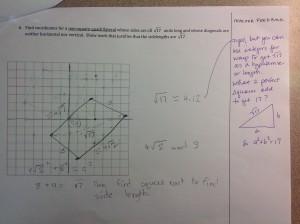
He had realized from his diagram that the two sides of the triangle would be equal and that if we wrote the equation of the perpendicular bisector of the base of the isosceles triangle and found its y-intercept he would find the depth of the water.  He proceeded to find the midpoint of the base, then the slope of the base, took the opposite reciprocal and then evaluated the line at x=0 to find the y-intercept.  I was pretty impressed – I had never seen a student take this perspective on this problem before.

This made my whole day – I was really dreading going back to work after vacation and honestly, first period was the best class of the day when this wonderful, new method was shown to me and this great experience of this student’s persistence refreshed my hope and interest in this problem.  Perpendicular bisectors are the new Pythagorean Theorem!

Someday I’ll get this assessment thing right… (Part 2 of giving feedback before grades)

3 Comments

So, all assessments are back to the students, tears have been dried and we are now onto our next problem set (what we are calling these assessments).  What we’ve learned is that the rubric allowed us to easily see when a student had good conceptual understanding but perhaps lower skill levels (what we are used to calling “careless mistakes” or worse). We could also quickly see which problems many students had issue with once we compared the rubrics because, for example, problem number 6 was showing up quite often in the 1 row of the conceptual column.  This information was really valuable to us.  However, one thing we didn’t do was take pictures of all of this information to see if we could have a record of the student growth over the whole year. Perhaps an electronic method of grading – a shared google sheet for each student or something to that effect  might be helpful in the future – but not this day (as Aragorn says) – way too much going on right now.

We also changed the rubric a bit for a few reasons.  First, we found that when students completed the problem to our expectations on the initial attempt we felt that they should just receive 3’s for the other two categories automatically.  We considered not scoring them in this category but numerically felt that it was actually putting students who correctly completed a problem at a disadvantage (giving them fewer overall points in the end). Second, we also changed the idea that if you did not write anything on the revisions you earned 0 points for the revisions columns.  Many students told me afterwards that they felt like they just ran out of time on the revisions and actually had read the feedback.  This was unfortunate to me since we had spent so long writing up the feedback in the hope that the learning experience would continue while doing revisions.

Here is the new version of the rubric: Revised Problem Set Grading Rubric new

What we decided to do was to try the revisions this time without the “explanation” part of writing.  I think it will keep the students focused on reading the comments and attempting a new solution.  I was frankly surprised at how many students stuck to the honor pledge and really did not talk to each other (as they still got the problem wrong the second time around – with feedback).  Truly impressive self-control from the students in my classes and how they were sincerely trying to use the experience as a learning opportunity.

I do think the second assessment will go more smoothly as I am better at doing the feedback and the rubric grading.  The students are now familiar with what we are looking for and how we will count the revisions and their work during that time.  Overall, I am excited about the response we’ve received from the kids and hope that this second time is a little less time-consuming.  If not, maybe I’ll just pull my hair out but I’ll probably keep doing this!

 

 

 

Why Teachers Don’t Give Feedback instead of Grades, and Why We Should

7 Comments

First in a series of posts about my experiences with “Feedback Before Grades”

Holy Mackerel is all I have to say – Ok, well, no I have plenty more to say – but after about a week and a half of holing myself up with my colleague, Kristen McVaugh, (big shout-out to Ms McVaugh who is not only teaching PBL for the first time but was willing to dive into this amazing journey of alternative assessment with me this year too), I am totally exhausted, almost blind as a bat, partially jaded and crazy – but mostly ready for a drink.  This little looped video of Nathaniel Rateliff and the Night Sweats pretty much sums it up…

So here was our well-intentioned plan:  we wanted to start the year off with a different type of assessment.  I put out my feelers on twitter and asked around if anyone had a rubric for grading assessments where the teacher first gave only feedback and then allowed students to do revisions and then once the revisions were done the students received a grade. Kristen and I knew a few things:

  1. we wanted to make sure the revisions were done in class
  2. we wanted to make sure the revisions were the students’ own work (tough one)
  3. we wanted to give students feedback that they needed to interpret as helpful so that we weren’t giving them the answer – so that it was still assessing their knowledge the second time around
  4. we wanted to make sure that students were actually learning during the assessment
  5. we wanted students to view the assessment as a learning experience
  6. we wanted students to be rewarded for both conceptual knowledge and their skills in the problem solving too

So we created this rubric Initial Draft of Rubric for Grading.  It allowed us to look at the initial conceptual understanding the student came to the problem set with and also the initial skill level. Kristen and I spent hours and hours writing feedback on the students’ papers regarding their errors, good work and what revisions needed to be done in a back-handed sort of way.

Here are some examples:

Student 1 Initial Work
Student 2s initial work
Student 3 initial work

 

Some kids’ work warranted more writing and some warranted less.  Of course if it was wonderful we just wrote something like, excellent work and perhaps wrote and extension question.  The hard part was filling out the rubric.  So for example, I’ll take Student 3’s work on problem 6 which is the last one above. Here is the rubric filled out for him:

Student 3’s Rubric

You will notice that I put problem 6 as a 1 for conceptual understanding and a 2 for skill level (in purple). In this problem students were asked to find a non-square quadrilateral with side lengths of sqrt(17).  Student 3 was definitely able to find vertices of a quadrilateral, but he was unable to use the PT to find common lengths of sides.  I gave him feedback that looking at sqrt(17) as a hypotenuse of a right triangle (as we had done in class) would help a bit and even wrote the PT with 17 as the hypotenuse in the hope of stimulating his memory when he did the revisions.

The day of the revisions Student 3 was only capable of producing this:

Student 3 revisions

He followed my direction and used 4 and 1 (which are two integers that give a hypotenuse of 17, but did not complete the problem by getting all side lengths the same. In fact, conceptually he kind of missed the boat on the fact that the sqrt(17) was supposed to be the side of the quadrilateral altogether.

 

One success story was Student 2.  She also did this problem incorrectly at first by realizing that you could use 4 and 1 as the sides of a right triangle with sqrt(17) as the hypotenuse but never found the coordinates of the vertices for me. I gave her feedback saying there might be an easier way to do this because she needed vertices.  However, she was able to produce this:

Student 2s revision
Student 2s revision

Although she did not give me integer-valued coordinates (which was not required) and she approximated which officially would not really give sqrt(17) lengths it came pretty darn close! I was impressed with the ingenuity and risk-taking that she used and the conceptual knowledge plus the skill-level. Yes, most other kids just used some combination of 1’s and 4’s all the way around but she followed her own thought pattern and did it this way.  Kudos to student 2 in my book.

Next time I will talk about some of the lessons we learned, other artifacts from the kids’ work and what we are changing for next time! Oh yeah and some great martini recipes!

Why PBL Works for Introverts

My school year is underway and as September just flew by, I have been completely overwhelmed by work – of course.  I am undertaking a new assessment method with a colleague of “feedback first and then grades” (blogpost to come when I give back the first set next week) but for now I wanted to comment on an article I just read this morning entitled “When Schools Overlook Introverts” that was posted on the Atlantic’s website.  This is a very thoughtfully written piece by Michael Godsey that is discussing how so much education is based on the idea of social constructivism which might be hard on those of us who are built to work best in “quieter, low-key environments.” This implies that the environments of collaboration and working with others are always loud, chaotic and multi-faceted.

And you know, sometimes it is.  Classrooms where kids are all at the board or working with technology can be messy.  Everyone’s talking at once, kids are calling me over and asking questions out loud (often the same questions 5 times in a row) and they are seeing themselves as the center of attention.  Once they understand, they move on and help their partner move on.  In my classroom, they take pictures with their iPads, record work in Notability or use GeoGebra to get a different perspective – either algebraic or geometric.  This can be quite chaotic.

However, most of the time in the PBL classroom.  everyone is required to sit quietly and listen to one student describe their thought process.  They need to learn to sit patiently while another student works though confusion and misunderstanding and ask questions of the presenter.  An introvert has a great deal of time of quiet to themselves being inside their head while the presenter is discussing his or her own grappling with a problem from the night before and the introvert can sit there and think, “Huh, that’s not what I did.  Should I say something and comment, or just accept that as the right answer?” The introvert grapples with different demons in the PBL classroom if they are a strong mathematics student in many ways because they might feel confident in the material but not confident that people care about their ideas.  Who knows?  It depends on their personality.

The introvert also has the opportunity to write journal entries for me and also to write bi-weekly learning reflections about what his or her learning successes were for the week.  This year I have a student with a speech impediment who was upfront with me about it at the beginning of the year.  This student has quickly become one of my best communicators because he realized how much I value what he has to say and that I would be patient and so would the rest of the class.  If he can’t say what he needs to say at the moment he wants to in class, he will always have an opportunity each week to do it.

I am very clear on my classroom contribution Assessment Rubrics that the grade does not depend on quantity of contribution, but quality.  Introverts should contribute because they have something important to add, an excellent question to make a clarifying point or something that will add depth to the conversation – never just to add to their grade. They can look at what they need to improve on by using my Student Analysis of Contribution which I will be doing next week – it’s about that time of the term.

I believe that although PBL strives to allow for all voices to be heard (both extrovert and introvert) it is the teacher that makes or breaks the classroom culture.  We need to be continually checking and rechecking the barometer of communication and tone of the class to be sure to all students are feeling heard. So that as Godsey says at the end of his article, the kids can learn with others and not by the “hell of other people.”

 

Disruption in Presence: Missing PBL Math Class

What do we all do with kids who miss out on the wonderful rich discussions where the learning happens in a PBL math class? @0mod3 asks what to do about kids’ absences. (thanks for the great question!)

It’s not as simple as “get the notes from somebody who was there” is it?  What did they actually miss by not being in class? Yes, new vocabulary possibly, new concepts, whether their problems were right or wrong – these things can all be “looked up” in some ways in another students notes or with a conversation with the teacher or a tutor just like in any other mathematics class.  So what is it we are really concerned with that they missed?

It seems that DReycer is hitting the nail on the head in her second tweet here.  Of course, it’s the experience of being a part of the rich mathematical discussions.  Hearing other students’ ideas and deciding for themselves or analyzing critically in the moment what they think of those ideas – is it right? wrong? potentially right? more efficient? similar to what I did?  These experiences are very hard to re-simulate for students who are absent from the PBL classroom.

When students come to me who have missed class.  I do tell them to look at other students’ notes.  However, this is because of how I tell students in my classes to take notes.  Kids are supposed to attempt the homework problems on one side of the notebook and then on the other side take “note of” what the other student who is presenting the problem did differently from them.  Eventually when we, as a class, come to some type of consensus about how the problem connects to a new concept or to a problem we have already done, it is then that a student should take note of the new idea as we formalize it into a theorem or new idea.

Absences will always be a problem for us who teach in the PBL classroom since we can’t recreate the in-the-moment learning that happens when a student sees another’s presentation (unless you feel like having parental consent for recording every single class, and even then you can’t really have the interaction with the student that missed it) however, what you can do is make the most of the time when each kid is there. PBL is by its nature relational learning and student and teacher presence is extremely important.  Be sure that students are the ones who are talking and asking questions in order for them to actively be engaging with the presenter.  Be sure that you are present to their needs when they return from an absence.  On days when they are not there, it might be enough for them to ask questions on the next day after they have read through the vocabulary or seen someone’s complete solution.  Sometimes active learning the next day can just be enough.

I’d love to hear other people’s ideas and thoughts!

Virtual Hand-outs for #GlobalMathDept conference

So tonight I give my very first online talk – I’m a little worried that talking to my computer will be a little strange at 9:00 at night, but we’ll see what happens.  Hopefully, there will be some type of audience interaction.  I’m such a relational person that I think I’m one of those people that really needs feedback will I’m talking.  We’ll see!

My hope is to discuss the differences between PBL & PjBL and how people can find a way to make some type of PBL work in their classroom no matter what place they are at in their teaching.

Here are the documents that I will be mostly referencing.  Hope to see you all there!

Student Self-Report on Class Contribution
Thinking_About_Thinking_Problem_Solving_Tool
Weekly Learning Reflection Sheet
Keeping a Journal for Math Class

Connections Between IBL and PBL

At the PBL Summit a few weeks ago, we had two wonderful speakers, Julian Fleron and Phil Hotchkiss from Westfield State University who are founding members of the Discovering the Art of Mathematics Project.  They gave a great key note address on Friday night about Inquiry-Based Learning and motivating students in an IBL classroom.  You can find their talk at our Summit Resources website if you are interested.  I wrote a blogpost a few years ago about my interest in IBL and the commonalities between PBL and IBL and I thought I’d reshare in honor of them.  Enjoy!

A number of years ago, I needed some kind of suport text for a Number Theory tutorial that I was doing with two rather advanced students who had gone through the curriculum at the school where I was teaching.  These two girls were advanced enough that I knew that if I used my notes and problems from my wonderful Number Theory course from college (some many years ago) we would have a great time.  I looked online and found a great book called “Number Theory Through Inquiry” published by the MAA which came with an instructor’s supplement including pedagogical discussion and some solutions.  It sounded so much like what I was doing with my other classes that I couldn’t turn down the opportunity to see what it was like.  So I ordered the book and while I was reading the instructor’s supplement I came across something that I had not heard about before (and now I am so embarrassed to admit this). The authors described what they called the “Modified Moore Method” of instruction or Inquiry-Based Learning and went on to describe what sounded interestingly so much like what I was doing in my classroom.  I had to learn about this Moore Method.

I ended up researching R.L. Moore online and it seems that he was one of the first math teachers – ever – to think about and act on this idea of not teaching mathematics with direct instruction.  He did it all the way back in 1948, but at the college level – and it was radical there!  The idea of Inquiry-Based Learning has expanded from there, but it has really only stayed at the college level in mathematics for a very long time.  There are many initiatives at the college level, including the folks at Westfield State University who are writing a wonderful curriculum project funded by the NSF called Discovering the Art of Mathematics with is a math for liberal arts curriculum at the college level.  I think it could be used at the secondary level as well for an alternative elective in the senior year for those students who still want to take a college-level math course but aren’t ready for or interested in an AP course in Calculus or Stats.  If there are any secondary teachers interested in beta-testing this unique curriculum please contact me and let me know.  I am on the advisory board for this project.

What made me think about the connection between IBL and PBL was this wonderful blogpost I just read by Dana Ernst, of Northern Arizona University in which he describes, in such wonderful ways, the pedagogy and nature of IBL.  The similarities between the definition of IBL he cites (by E. Lee May) and my definition of PBL are eerie – and it is one of the only ones that I’ve seen that stresses a reference to teacher authority being diminished.  Many wonderful resources are given by Ernst at the end of his post as well.

I do remember back in 2003, when I published my first article on my experiences at Emma Willard, after I left Exeter (where they called in Harkness teaching because of the table), in attempting to teach the way I wished to.  I had no idea what to call what I was doing.  I believe in my first article I called it teaching with a Problem-Solving Curriculum (PSC).  After I started my doctoral work, I found PBL and I realized that’s what it was.  Then I read more and more and realized that others thought PBL was project-based learning and called what I did discovery learning.  After reading about R.L. Moore, it sounds like he was doing it all along since 1948 and called it IBL.  In whatever branch of the pedagogical family tree you find yourself, if you are asking students to look at mathematics with wonder and question what they know – you should know that you are supported, know that you are doing good work and know that there is someone out there who has done it before and wants to discuss it with you.

PS – I’m hoping to attend the Legacy of R.L. Moore Conference next year in Austin, if anyone is interested!

Think about where the learning happens in PBL

2 Comments

After a few weeks of recovery, I wanted to write about having a BLAST of a time at our first attempt of putting together the PBL Summit my friend Nils Ahbel and I organized from July 16-19.  I wanted to thank all of those who came and participated in the discussions and talks and who shared their ideas so freely.  It’s such a great reminder of the huge resources we all are to each other as math teachers.  I know that I at least tripled my Professional Learning Network and hope that all of the participants did too.

I’d also like to thank everyone who gave feedback and the amazing ideas for next year – including a pre-conference session for those of you who might have been PBL “newbies” and might have needed more of an intro, topic-level groups, more in-depth SIGs for people who want to dive deeply into writing or assessment writing too.  The ideas just kept flowing and I think we will have a wonderful plan for next year too.

One of the take-aways that I left the PBL Summit with was how differently people view what “learning” means in PBL.  From my long career both teaching and studying PBL, I have had a lot of time to form my own frameworks for student knowledge construction and pedagogical theory and often take for granted that all of us are on the same page. As I have traveled and talked to many other math teachers and heard others who are experts in PBL (both PjBL and PrBL) speak, I realize more and more that we are often NOT on the same page.  This does not mean that any one of us is more right or wrong.  We just need to understand each other more.

My big question to everyone I talk to is “where/when does the learning happen?” or “where/when do the students construct their knowledge and understanding of the mathematics?”  If students are presented with a problem, for example they watch a wonderful interesting video of a basketball player shooting at a basket or watching someone fill a water tank and they come up with their own question based on a real-life phenomenon from the video, how do those students know the mathematics to answer those interesting questions?  If students are sitting through direct instruction lessons to be exposed to the mathematics but using them to answer their own questions, this is definitely an improvement than passive mathematics classes of the past.  Having students take ownership of the material in this way is is a powerful method of creating agency for mathematics learning.  The problems that they are solving and from where they are posed are extremely relevant to the motivation and agency in learning.

I would posit that PBL can be more and mean more and in more ways to student learning. Even when posed with a good problem (one they did not come up with themselves).  In PBL, students can:

  • see the need for a new method without the teacher introducing it
  • see the need for discussing other students’ ideas
  • find their own organizational strategies for problem solving
  • access prior knowledge that they did not realize they needed before
  • use their resources to discuss the problem with each other
  • use resources to find new solutions and follow their own thinking
  • make connections between topics in mathematics that they might not have realized before
  • create community in the mathematics classroom (like in other disciplines – humanities, fine arts and science)
  • realize that reflection is one of the most important parts of the learning process
  • learn to relate to others in math class
  • see mathematics as a creative endeavor

and so much more. I’d love to hear from people some that I have left out.  In my mind, even the mathematical learning happens in these contexts and students are the shapers of where and when this happens.  Robert Kaplinsky is one of those amazing PBL teacher/speakers who has a somewhat different approach than I do, but is very similar in many ways and I heard him say this April, “Don’t teach what students need to know before they do a problem-based lesson.” In that way, we are all on the same page, for sure.

One of the Original “Makers”

Apologies to any faithful readers out there – I have had a heck of a summer – way too much going on.  Usually during the summer, I keep up with my blog much more because I am doing such interesting readings and teaching conferences, etc. (although I’m running a conference for the first time in my life!) However, this summer I was dealing with one of my biggest losses – the passing of my father after his 8 year battle with breast cancer.  I thought I would honor him by writing a post talking about a problem that I wrote a few years ago, well actually a series of problems that utilized his work when teachers of algebra I asked me how I taught the concept of slope.  So dad, this one’s for you.

In 1986, my dad, Francesco (Frank) Schettino, was asked to work on the renovations for the centennial project for the Statue of Liberty.  He was a structural steel detailer (also known as a draftsman) but he was really good at his job.  Everywhere we went with my dad when I was younger, he would stop and comment about the way buildings were built or if the structure of some stairs, windows or door frames was out of wack.  He could tell you if something was going to fall down in 10 years, just by looking at it.  At his wake last week, one of the project managers from a steel construction company that he worked on jobs for told me that they would save the interesting, most challenging jobs for him because they knew he would love it and do it right.
photo (1)I remember sitting with my dad at his huge drafting desk and seeing the drawings of the spiral stairs in the Statue of Liberty.  He talked to me about the trigonometry and the geometry of the circles that were necessary for the widths that were regulated for the number of people that they needed to walk up and down the stairs.  This all blew my mind at the time – that he needed to consider all of this.  So to be able to write problems that introduce slope to students about this was just a bit simpler to me.

If you take a look at my motivational problems on slope and equations of lines I believe it’s numbers 2 and 3 that refer to his work (excuse the small typo).  Over the years I’ve meant to go back and edit these a number of times.  If you are someone who has taken my course at the Anja S. Greer Math, Science and Technology Conference at Exeter, you are probably familiar with this series of questions because we have discussed these at length and talked about how students have reacted to them (and how different adult teacher-students have as well).  We have assumed no prior knowledge of slope (especially the formula) or the terminology at all.

Some questions that have come up: (with both students and the teacher-students I’ve worked with)

1. What does a graphical representation of “stairs” mean to students?
2. What does “steeper” mean and what causes stairs to be steep?
3.  Why are we given the “average” horizontal run for the spiral stairs? Would another measurement be better?
4. Why does the problem ask for the rise/run ratios?  Is there a better way to measure steepness?
5. (from a teacher perspective) why introduce the term “slope” in #3? can we just keep calling it steepness?

These are such rich and interesting questions. The questions of scaffolding terminology and when and how to introduce concepts are always the most difficult.  Those we grapple with specifically for our own students.  I always err on the side of allowing them to keep calling it steepness as long as they want, but as soon as we need to start generalizing to the abstract idea of the equation of the line or coming up with how to calculate that “steepness” a common language of mathematics will be necessary.  This is also where I take a lesson from my dad in terms of my teaching.  His great parenting style was to listen to me and my sisters and see where we were at – how much did we know about a certain situation and how we were going to handle it.  If he felt like we knew what we were doing, he might wait and see how it turned out instead of jumping in and giving advice.  However, if he was really worried about what was going to happen, he wouldn’t hesitate to say something like “Well, I don’t know…”  His subtle concern but growing wisdom always let us know that there was something wrong in our logic but that he also trusted us to think things through – but we knew that he was always there to support and guide.  There’s definitely been a bit of his influence in my career and maybe now in yours too.

Late night thoughts on Assessing Prior Knowledge

2 Comments

So it’s 11:50 pm on a Tuesday night, so what?  I can still think critically, right?  It was the last day of classes and I had an amazing day, but then all of a sudden Twitter started gearing up and lots of discussions began and my mind started racing.  I had planned on writing a blogpost about a student’s awesome inquiry project (which, it ends up, took me about 2 hours to figure out a way to make an iBook on my iPad into a video to try to post on my blog, so that will have to wait), but then I read a great post by Andrew Shauver (@hs_math_physics)

Mr. Shauver writes about the pros and cons of direct instruction vs. inquiry learning but has a great balanced viewpoint towards both of them. In this post, he is discussing the how and when teachers should or can use either method of instruction.  It is important, Shauver states to remember that “inquiry can work provided that students possess the appropriate background knowledge.”

I would totally agree, but I’m just wondering how we assess that – does it really work to lecture for a day and then say they now possess the appropriate background knowledge?  Do we lecture for two days and then give them a quiz and now we know they possess it?  I wonder how we know?  At some point, don’t we have to look at each student as an individual and think about what they are capable of bringing to a mathematical task?  We should set up the problems so that there is some sort of triggering of prior knowledge, communication between peers, resources available for them to recall the information?

Joseph Mellor makes a great point that in PBL most of the time you might plan a certain outcome from a problem, or set of problems, but the triggering didn’t work, or the kids didn’t have the prior knowledge that you thought.  He says that he is often either pleasantly surprised by their ability to move forward or surprised at how much they lack. In PBL, we depend on the students’ ability to communicate with each other, ask deep questions and take risks – often admitting when they don’t remember prior knowledge – hopefully to no suffering on their part. This can be a big hurdle to overcome and can often lead to further scaffolding, a deeper look at the writing of the problem sequence, fine tuning the awareness of their true prior knowledge (not just what the previous teacher said they “learned”) or yes, maybe a little direct instruction in some creative ways.  However, I do believe that given the opportunity a lot of students can be pleasantly surprising.  What do you think?