Author: Carmel

Teaching Pythagorean Distance with PBL

This is going to be the first of a series of commentary posts on the types of problems that I help teachers learn to use to teach math with problem-based learning.  The type of PBL that I am a supporter of is what I call Relational Problem-Based Learning in which the construction of knowledge comes from the discussion of scaffolded problems.  I’ll give specific examples of the problems that the students and teacher discuss and the ways in which the discussion builds on prior knowledge.

A great example of this is the way that the Pythagorean Theorem and the concept of Pythagorean Distace are connected so nicely. The prior knowledge that is assumed (and triggered with basic problems of finding legs, hypotenuses, simplifying radicals, etc.) is basic use of the Pythagorean Theorem.

Number 9 in the Avenues Math 2 book (adapted from the PEA Materials) says:

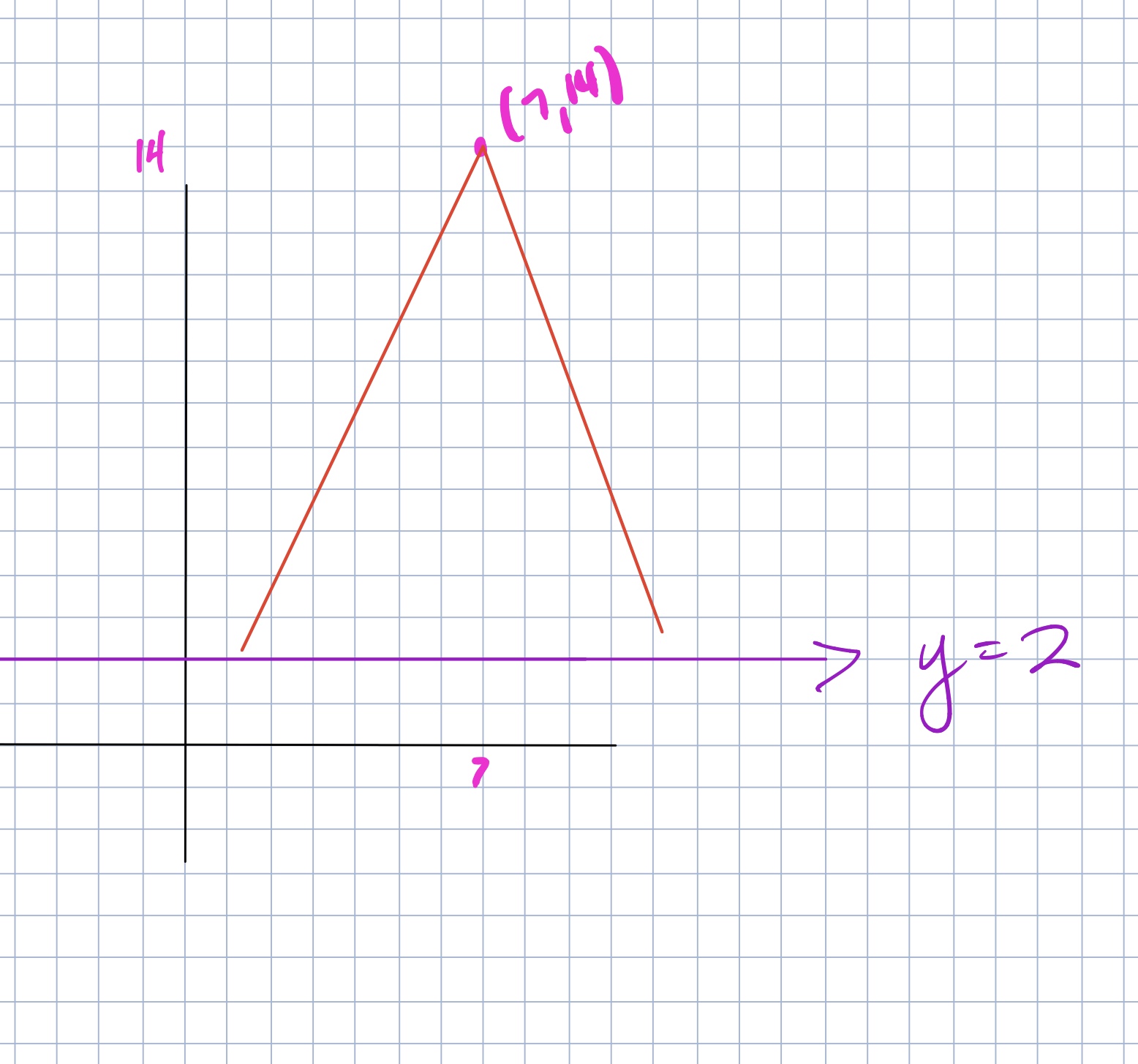
Two different points on the line y = 2 are each exactly 13 units from the point (7, 14). Draw a picture of this situation, and then find the coordinates of these points.

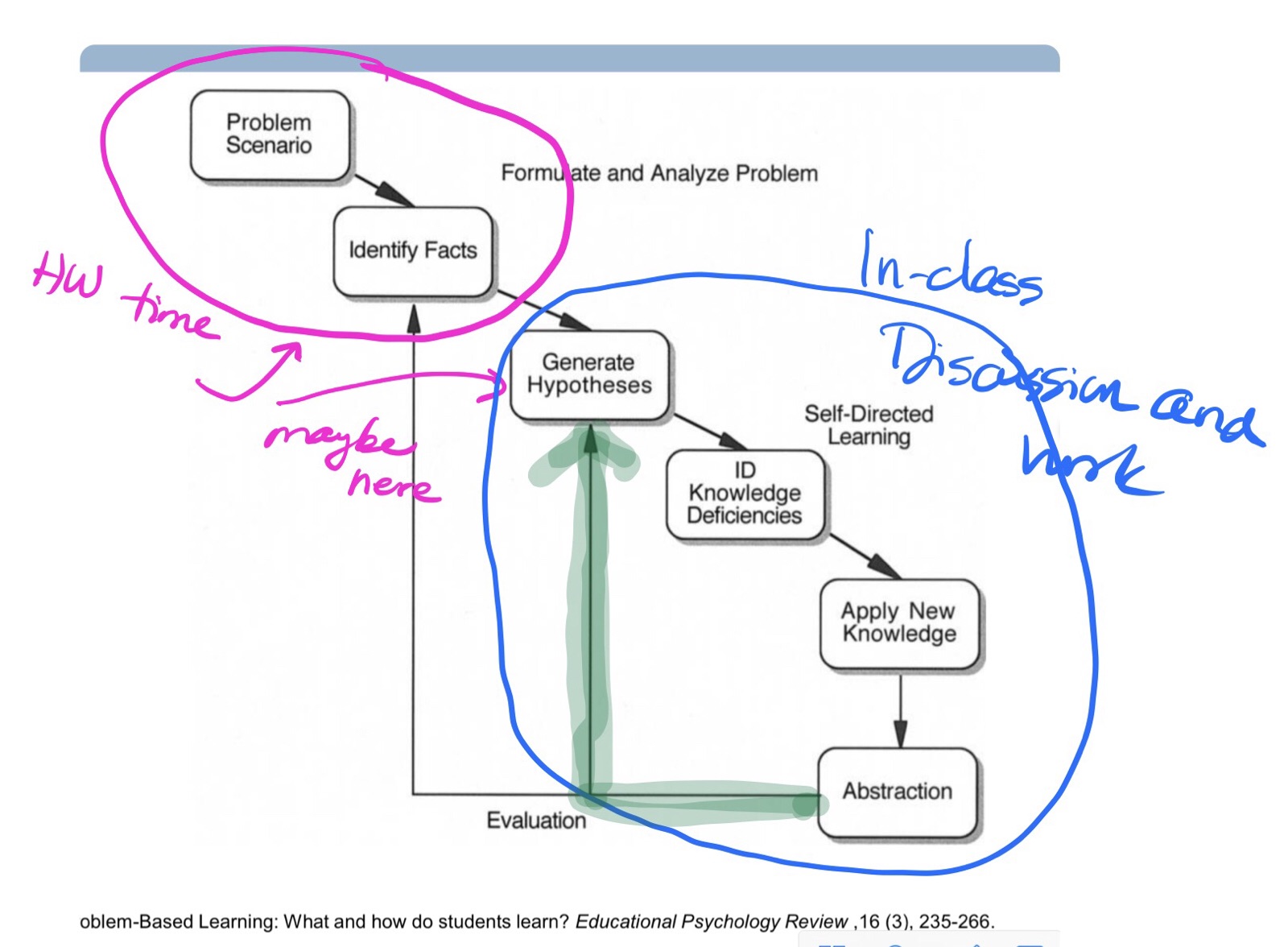
This problem is usually done within the first week or so of school. When doing this problem for homework without having previously discussed something like this in class, many students are capalble of graphing the line y=2 (although you can probably guess the most common error!) and the point (7,14).  However, many students often are still confused about what the distance “13 units” means. Many student come to class with something like this, which is a totally acceptable attempt actually.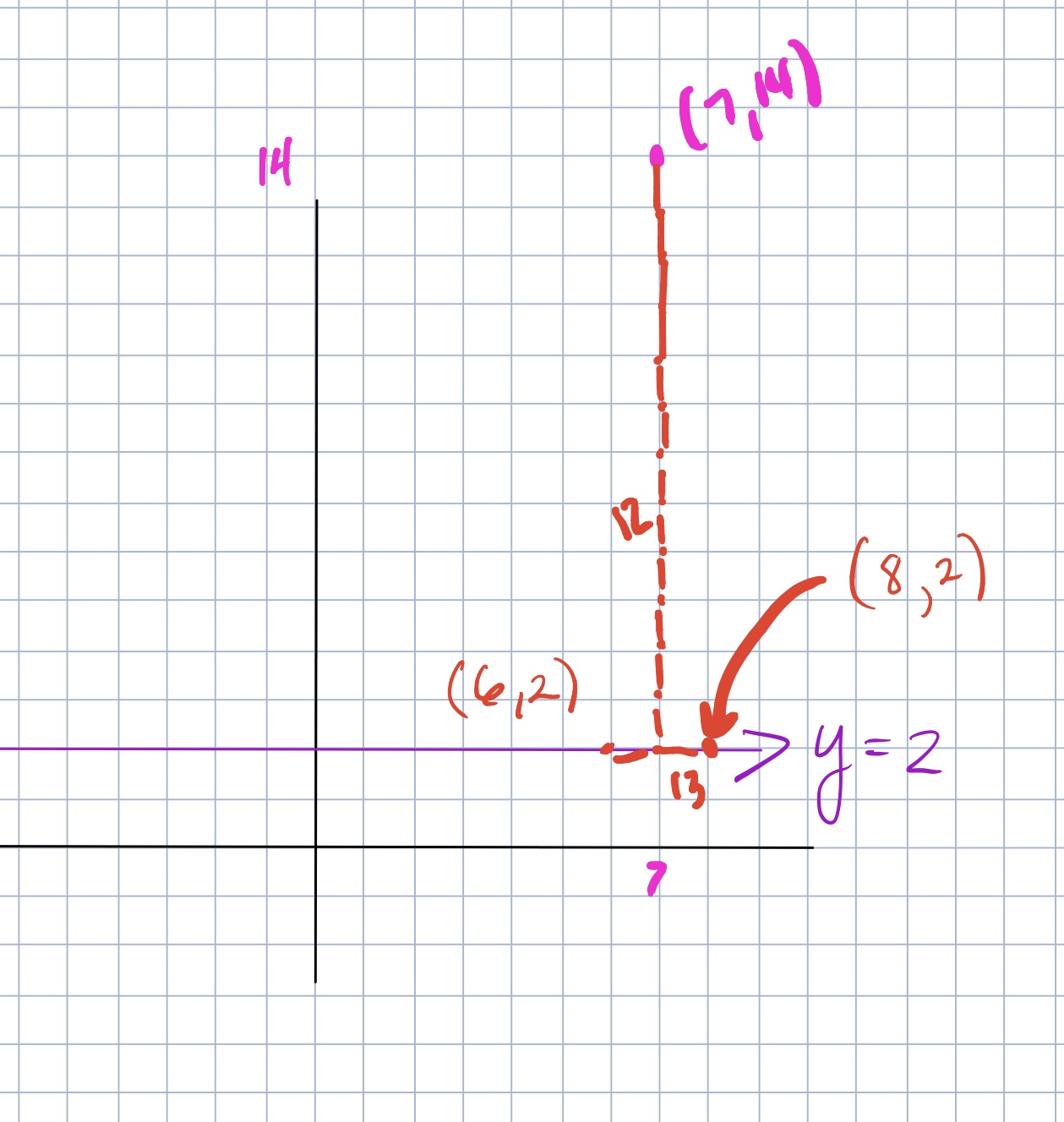

This first attempt is a great conversation starter about what Pythagorean distance in the geometry that we are studying means.  In fact for any kids who live in a city, it’s a great opportunity to talk about “Taxi-Cab” Geometry and how that is a different way of measuring distance.  The interesting thing is that many students who come to class with this type of inital definition of distance oftentimes live in a city.  I find it really important to validate their idea of distance but just to say that it’s just not the Pythagorean Definition of distance and if they want to learn more about Taxi-Cab Distance, I have readings on it. (see here and here).  This is consistent with Chris Emdin’s opening talk at the NCTM annual this year about privileging all students intuition about math.

Generally, the discussion that follows is that some other students says that they did not think of the distance that way.  They saw it “straight” there.  If not other students says this, which is usually rare, but could happen, Then it is the teachers responsibility to bring up the idea of a more direct distance.  What I usually do is ask “What other ways are there to think about distance?” Some student usually says something like “as the crow flies” or “straight there” – which is really funny.  They have the idea but don’t really know how to say what they mean.

They can sometimes draw a picture like this:

But the idea that they need to figure out the coordinates that are on the line y=2 is very difficult.  The students don’t know where to put the points there on the line y=2, so it’s hard for them to label them – what do they do?  At this point, if a student can’t say that the distance is supposed to be 13.  They need a question that is leading them to the right direction.  A few different directions can be taken:

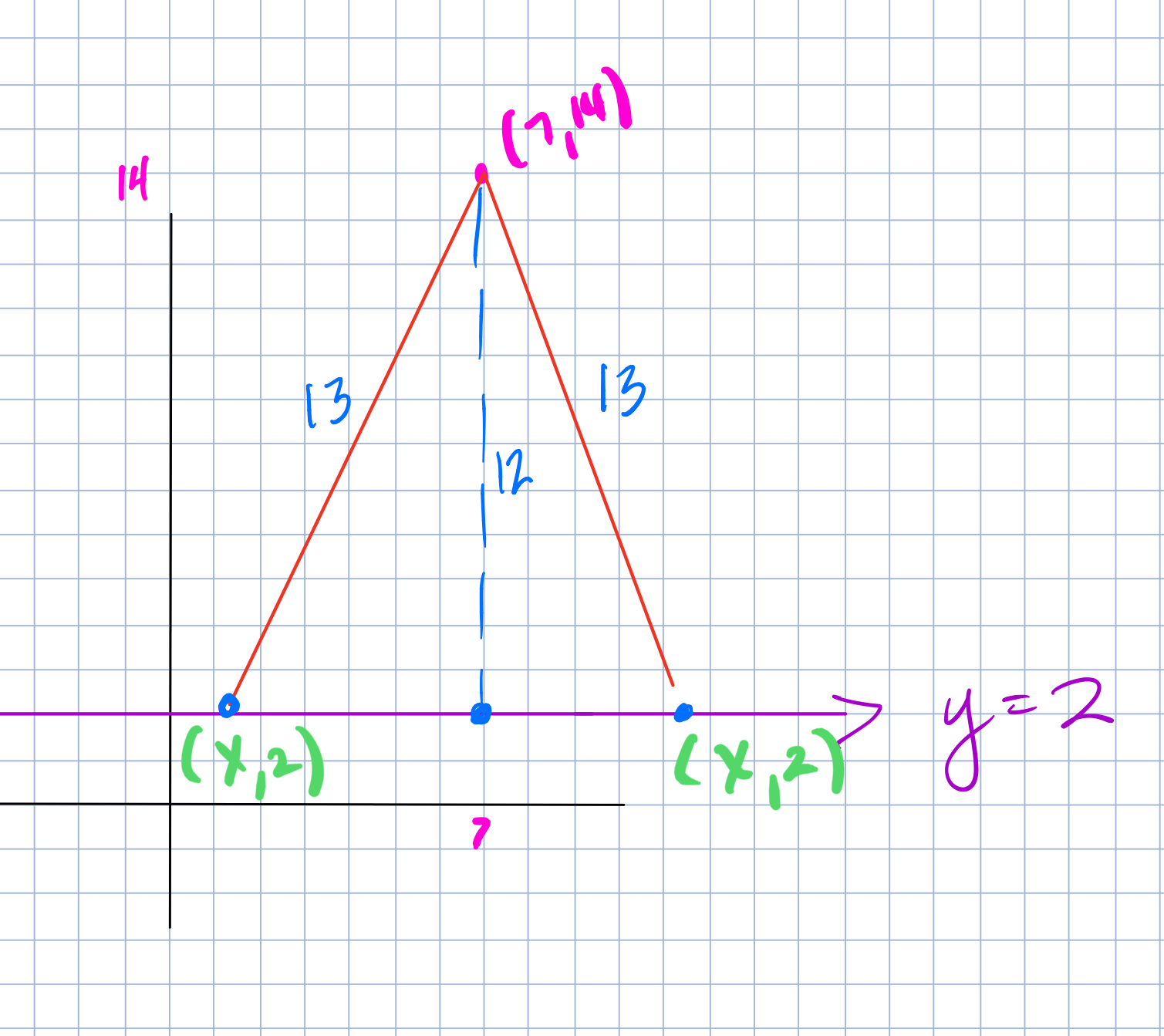
  1. Ask the students if the fact that the vertical direction was 12 is helpful at all – that was something that a student realized and is actually important to the solution of the problem.
  2. Ask the students where the distance that is supposed to be 13 is represented in the diagram they’ve drawn now
  3. have the students turn and talk to each other to think about ways in which they might visualize the “two different points that are 13 units away”

In my experience, what follows from these teacher actions is some productive struggle, as long as you are patient.  When students get to this point:

The next difficulty is figuring out the coordinates.  This is where the Pythagorean Theorem comes in.  Even if the students can see the 12 and the 13, it might be difficult for them to get to the point where they realize that there is a right triangle in the diagram.  This should be a whole class conversation in order to optimize the likelihood of a student seeing the right angle.  Finding the missing side, does not even guarantee being able to find the coordinates.

So in order to have students to be able to add and subtract 5 from 7, students need to be able to have the coordinates of the point that is directly below (7,14) on the line y=2, which is (7,2).  I always try my hardest not to just come out and ask “What are the coordiantes of the point right below (7,14) becasue that is just basically telling them what they need to find.  I try to ask them what do they need to know in order to find the coordinates.

It is very satisfying when students finally see that it is really just an application of the Pythagorean Theorem.  I wrote a blogpost about one conversation with a student about just this problem a while ago.

Just another note on alternate perspectives:  I have had students do this by looking at this problem as a circle intersecting the line y=2.  Of coruse, they don’t know how to do that right now, but students who are technologically savvy end up doing in on geogebra and having stuch a great concept of what 13 units away means that they get the right answers without using the Pythagorean theorem.. It is a great way to try to get students to even see that the “radius” they are using is the hypotenuse of a right triangle.

Resources for my NCTM Conference Talk Washington 2018

I hope there’s lots of interest in the lessons that I’ve learned from my years of having students journal. Here are some resources that you could use if you are interested in trying journals in your math classes.

Handout for NCTM Session Handout Schettino NCTM 2018

Blogposts about Journaling:

journals-paper-vs-digital-the-pros-and-cons/

what-i-get-out-of-student-writing/

revisiting-journals-getting-kids-to-look-back/

does-journaling-in-pbl-promote-resilience/

using-journal-writing-in-pbl/

Page: metacognitive-journaling/

Slides for Talk: Slides from Journal Presentation

PBL: High Expectations or Learning to be Self-Directed?

One issue that seems to arise after teachers have been teaching with PBL for some time is the question of how students can remain active learners while listening, taking notes, comparing solutions, being engaged in discussion, etc.  All student-centered mathematics classrooms now have this issue don’t they?  Can a student learn well when they are being active in their learning? How do you allow them to both have agency by being part of the construction of knowledge but also have ownership by taking responsibility for the active part of learning.

Here’s a scenario: Grade 8 class has a student at the board presenting a method of factoring that is obviously confusing everyone – you know, they learned “the box method” somewhere else and are presenting it like it’s just a given that you are supposed to know this.  I’m observing this and I’m seeing at least 5-7 looks of confusion, maybe 1-2 students who are following the student and at least 3-4 who have checked out totally – maybe drawing a tree in their notebook.

How do you maximize this moment?  It is imperative that the teacher move in and ask questions that get at the student presenter’s understanding, especially if the other students are not asking questions.  There may be an air of “oh god, I’m supposed to understand what this kid is talking about” and others will not be asking good questions.

The teacher can ask questions like:

“OK, good work that you have a method that works for you.  Can you back up and explain how this method is showing what the factors of the quadratic are?”

“Let’s slow down a minute and see if there are any questions.”

“Why don’t you explain why you chose the number and variable you did for each box and what those boxes represent?”

“Can everyone else write down a question for …. and then we’ll share out.” (this can include making up a problem for those who do understand and seeing the presenter do another example)

These will bring the moment back to the group, wake them up to the fact that it’s OK to have questions and maybe an alternate method as well.  The kids who have checked out might feel validated in checking out.  But at the same time, checking out shouldn’t be an option. . How can we teach students to remain connected even when they really feel like all is lost?  In PBL, it is most important for student to have the tools in order to do this.

Today I saw this infographic tweeted by Brian Aspinall (@mraspinall) that does an excellent job of summing up ways to have students remain engaged when they want to check out.

Screen Shot 2018-02-23 at 2.59.57 PM

So many of these relate to the expectations for students in the PBL classroom.  Some of my favorites are

1. Reflect in writing – hugely important for the introverts in the PBL classroom and to share the floor and authority.

2. Relate it – not only to “something” you’ve experienced but another problem that you might have done that is connected to it!

3. Control your environment – How engaged you are is really your decision – How can students minimize their own distractions?  Of course day-to-day this will vary, and is developmentally different from grade 8-12 of course, but students, when aware of being distracted, can often find ways to get back into the work.

4. Self-Assess – this is one of my favorites – it keeps them engaged, makes them think critically and thinking ahead.

Allowing kids to know that doing all of these different behaviors in the math classroom is not only OK, but expected and encouraged, is part of teaching with PBL and encouraging the “active” in active learning.

Online Journal Course PreSale Going on Now

OK, so my online course for math teachers who are interested in learning about using meta cognitive journals is all ready to go. The official start day is next Friday Dec. 1, but if you register during this week prior, you get $50 off the full registration fee.

Click here for information on registering: Registration with Coupon

Here’s a description of the course if you are interested:
This course is an on-demand course geared towards middle and high school mathematics teachers who want to learn about journal writing in math classes. There are four main course lessons that range from the reasoning of using journals to how to assess them. Interaction can occur between participants in this course via the discussion forums with as much or as little time committment as participants desire.

Please share with anyone you might think is interested in learning about using journals in math class. Thanks so much!

The “Wounded Healer” Archetype in the PBL Teacher

4 Comments

I have been doing a lot more work with teachers this year as I am not in the classroom.  I love watching people teach and talking to them about their teaching.  It is clearly a passion for so many people and the modeling of lifelong learning has been so inspirational for me and their students.

One issue that seems to arise in all PBL classrooms, no matter how progressive the teacher, is this feeling that they need to somehow, someday really just not allow the students to be frustrated.  Even those who buy into the whole PBL, student-centered, productive struggle pedagogy – deep inside they understand the belief from their own education, that math is black-and-white there needs to be some resolution that is acknolwedged and /or provided by the teacher.

I was talking to a friend about this dilemma a while ago (thanks @phiggiston!) and saying how interesting it is to me that a teacher’s belief from their past can, in the moment, while teaching, often override their beliefs in the current pedagogy.  In other words, if a teacher has not experienced independent learning as needed in PBL, it is extremely difficult to not give into the impulse to “save” the students from that feeling of struggle or unease.

Well, coincidentally, @phiggiston has a background in both religious work and in psychotherapy training, so the first the he says to me is, “it’s kind of like the patient-therapist relationship in a way.” And I’m thinking, my teaching is nothing like being a therapist, but of course, I listened intently.  I guess there is a Jungian theory that says that “sometimes a disease is the best training for a physician.”  In fact, Jung goes as far as to say that

“a good half of every treatment that probes at all deeply consists in the doctor examining himself, for only what he can put right in himself can he hope to put right in the patient.”

_____________________________________________________________________________

So what does this mean for PBL teaching?  I had to think of this for a while and also read some Jung as I am not up on the psychological theories that connect to education.  I wasn’t quite sure that this “Wounded Healter” achetype paralleled the PBL teacher as much as I originally thought.  Here are some points:

  • Jung says that for the wounded healer the therapeutic encounter should be regarded as a dialectical process  It’s not just I’m going to the doctor and she’s going to tell me what wrong with me.  There needs to be some kind of dialogue in order for a real healing to happen.  In the classroom, I would argue that this is true about the teacher-student relationship.  Traditionally, it has been that not having dialogue would result in learning that was not as long-lasting, effective and/or connected to the students own ideas.  It is pretty clear that the PBL teacher needs to create the dilectical process in order for the best learning to happen.
  • Jung argues that the physician must help create a safe space where the “patient’s “inner healer” is made available to her unconsciously.” At the same time the physician, should let go of the way she is activiated by the same wounds. This idea is extremely relevant in the PBL classroom.  Why do we want to make students comfortable and relieve their anxiety about mathematical learning?  My take would be because we hate the way it makes us feel. Knowing that struggle is all to close in our memory can actually help us hand over the power to “heal themselves.”  If we can get over that feeling, it will become more of the norm in the classroom.
  • There are risks to this type of teaching – the risk of being vulnerable because you are looking at your own wounds, and also looking fragile to the patient (or student).  This is a very common concern of teachers who are beginning PBL teaching.

“The experience of being wounded does not make him/her less capable of taking care of the patient’s disease; on the contrary, it makes him/her a companion to the patient, no longer acting as his/her superior.”

In other words, it is worth the experience of creating that open relationship.  I go back to Hawkins’ theory of learning (I-thou-It) in which the relationships that exist form a triangle between teacher-student-material.

Hawkins (1974)
Hawkins (1974)

All of these relationships must be nurtured in order for the best learning environment to exist. (For more on this check out Carol Rodgers presentation slides here.)

_____________________________________________________________________________

So does this mean if you did not have this type of experience learning math that you can’t learn to empower your own students in this way?  I think not.  When I ilook back on my own mathematical experiences many of them were extremely traditionally taught.  However, I think what you need to have inside you is both the belief that students are capable of owning and constructing their own knowledge and the ability to create a space that allows them to remain uncomfortable.  You have to be willing to let go of your own insecurities and anxieties about learning math and realize that the more you do that, the more the students will feel it as well.

I am currently working on a quasi-research project about this and when/how PBL teachers choose to intervene in class discussion.  If there is anyone who is interested in helping me out with this, I’d really appreciate it.

Reducing Cognitive Load in PBL

2 Comments

One of the things that I have been thinking about for a very long time is the idea of those who oppose PBL.  Namely those who prescribe to behaviorist and cognitive scientist theories of learning, which I know a great deal about because of my doctoral work.  So many teachers, parents and others have asked me about this over the past 25 years that you’d think I would have an answer.  I know I have thoughts but I do want to do more research in this area.

I do not pay lip-service to the ideas of cognitive load theory for sure and definitely respect those who follow these ideas.  I do think there is a place for thinking about this theory in PBL, but not an argument for why NOT to do it.  At its heart though, I believe the learning outcomes that are important in the different types of theory (CLT vs. constructivist learning for example) is what ends up differentiating them and also the way the knowledge is constructed.  I do believe in the importance of reducing the Cognitive Load for students so that their long-term memory can be triggered and practiced.

So I do believe there is a place for this in PBL – it just hasn’t been discussed a great deal.  There is always this us vs. them notion that one is right and the other is wrong – it comes from very strong belief systems and I totally understand where they are coming from.  However, if PBL is done well in a scaffolded, structured way, I believe that you can both reduce cognitive load and also ask students to think creatively.

Here is an image I saw from an article in the Guardian recently entitled Teachers: Your Guide to Learning Strategies that Really Work by Carl Hendrick. This graphic is describing the six ways to make your classroom best-ready for learning.

 

Positive Class room climate

 

When I was looking at this, the first thing I thought of is “This is my PBL classroom.”  However, I could tell there would have to be some discussion of the “reducing cognitive load” part.  All the other aspects, I believe you can find in some other blogpost of mine somewhere.  In a PBL classroom, the way that students get timely feedback is in so many ways (see my rubrics, journals, etc.).  The nightly homework is the scaffolding of learning and monitoring of independent practice – again when done well.  I won’t go through every one of these, but would love your takes (in the comments below) on each of them.

So then, how can we talk about reducing cognitive load in PBL – where is lecture and worked problems that the teacher does?  I would argue that the cognitive load is reduced by the scaffolding of the problems in the curriculum.  In other words, by triggering students’ prior knowledge the cognitive load is reduced in such a way that they are remembering something they have learned from the past, and then being asked to look at something new.  The “something new” goes through many phases of problems – concrete, multiple representations, all the way through to abstract – in order to slightly build up the cognitive load.  Again, this is all if it is done well and very deliberately with the idea of not to overload students’ thinking but to help to build the schemas that are needed for constructing knowledge both individually and socially.

The problems are worked by the students, yes – I will give you that.  But it is the teacher’s responsibility to make sure that the steps are correct, students get feedback on their thoughts and ideas, that on the board at the end of the discussion is a correct solution and so much more.  What this type of teaching does, in my view is both reduce cognitive load to a point, yet also allow students to gain agency and ownership of the material through their prior knowledge and experience.

Something else that Mr. Hendrick says in his article is:

“Getting students to a place where they can work independently is a hugely desired outcome, but perhaps not the best vehicle to get there. Providing worked examples and scaffolding in the short-term is a vital part of enabling students to succeed in the long-term.”

And I would ask, what does students’ success mean in this framework?  Some studies have shown that worked examples are beneficial in only some cases for student learning.  Others have shown that students that are taught with worked examples out-perform those who received individual instruction.  I could go on and on with the studies contradicting each other.  But what if they weren’t in contradiction?  What if there was a way that they could work together – both reducing cognitive load and also giving students agency and voice in the classroom?  Allowing students the freedom to become independent problem solvers but also scaffolding the learning in such a way that their cognition was not overloaded?  Maybe I’m an optimist, but I do believe there is a way to do both.

Looking at PBL Practice from a Thematic Perspective

2 Comments

So I’m here down in Florida – loving it (all sing-songy like Oprah would say).  I’ve been to so many talks that have been great learning experiences so far.  The weather is beautiful – I went for a very long walk and tried to think about what my talk was missing.  I did a bunch of edits and now I think I’m ready to post it.

Here’s the powerpoint of the talk:

Here’s the document that I handed out with some “threads” of themed topics:

Three Threads Document

Please contact me with any questions, comments or concerns – I love talking to people about PBL and my work.

How do you justify the time that PBL takes?

4 Comments

I just wanted to respond to a really great question that someone asked on Twitter the other day.

This is a common concern of teachers starting out with the idea of PBL. What does “Class Discussion” mean, first of all? I would agree that discussion does “eat up valuable” time in class on a daily basis, for sure. But what is actually happening in that discussion where something else would be normally happening in the math classroom? What does the discussion replace?

In my mind the discussion itself replaces the lecture, teachers ‘doing of problems” for the kids to then repeat, then kids often sitting on their own or in pairs doing problems that were just like the ones the teacher showed them how to do. The importance of the class discussion (which honestly is the main idea of PBL) is for students to share their ideas of prior knowledge, connections between problems, where they are confused and see where others were not confused and what prior knowledge and experience they brought to the problem.

Here’s a diagram that I use when doing PD work with PBL teachers to help explain all of what is supposed to be happening during class (it’s a lot!)


The student presentations are really just a jumping-off point. It is not just for students to explain “how they did a problem” – as they say – or they think what they’re supposed to do. The steps of Hmelo-Silver’s “process of learning in PBL” diagram that I’ve circled in pink is what students would/should do for homework. However, the part that is circled in blue is actually the learning process that happens in the class discussion – so is this time that has been “eaten up” in class or is it actually a very necessary part of the important learning, reflection and self-regulation of the process that needs to happen?

Is this harder for students? Heck, Yeah. There is so much more focus, listening, questioning and reflection that is needed in order for this process to be successful and productive. But there are ways to make it easier for students and that’s what the “class discussion” time is for. It takes a lot of practice and mastery on the teachers’ part to realize what is needed. Making mathematics discussion productive is a very important part of teaching in PBL and definitely not a part that should be seen as subtle, intuitive or straightforward.  There is so much more to this that I can not put in a single blog entry, but it’s definitely worth beginning the discussion.  Would love to hear others’ thoughts.

I’ve looked at life from both sides now…

4 Comments

This past July, I spent a few days at the MAA Mathfest in Chicago for the first time. The main reason I went was because the Academy of Inquiry-Based Learning was having a Conference within the Mathfest with the theme of “Diversity in IBL.”  IBL is generally what college faculty call the type of teaching and learning that many of us at the secondary level has been calling PBL for years.  I was so interested to hear many mathematics professors talking about the struggles of writing curriculum, dealing with facilitating discussion, using writing – all of the same parts of this type of teaching that we may have been talking about for so any years.  I highly suggest that we could benefit from talking to each other.  If you would like to get involved with this movement, Stan Yoshinobu, the Director of the Academy of Inquiry-Based Learning, has put forth some challenges for his community.  Check them out.

One of the most interesting talks that I attended was by a professor from Denison University, Lew Ludwig, titled, “Applying Cognitive Psychology to the Mathematics Classroom.”  As a devout social constructivist, I generally like going to talks where I can learn more about other views of education.  Seeing both sides definitely helps me understand many of the views of my colleagues and see if evidence supports my own perspective. Ludwig had published a review of another article that was titled, “Inexpensive techniques to improve education:  Applying cognitive psychology to enhance educational practice”(Roediger and Pye, 2012).

Basically, the presentation summarized three simple techniques that cognitive psychology had evidence helped student learning. The three techniques were called

  1. The distribution and interleaving of material and practice during learning.
  2. Frequent assessment of learning (test-enhanced learning, continual assessment)
  3. Explanatory questioning (elaborative interrogation and self explanation; having students ask themselves questions and provide answers or to explain to themselves why certain points are true).

In the original article, the authors write:

“Repetition of information improves learning and memory. No
surprise there. However, how information is repeated determines
the amount of improvement. If information is repeated back to back
(massed or blocked presentation), it is often learned quickly but
not very securely (i.e., the knowledge fades fast). If information is
repeated in a distributed fashion or spaced over time, it is learned
more slowly but is retained for much longer”

When this was reported, I was first in shock.  I couldn’t believe I was hearing something in a presentation about Cognitive Psychology that was actually supported by the definition of PBL that I use.  The curriculum I use takes the idea of looking at topics and teaching them over a longer time span, but distributed among other topics.  I have called this decompartmentalization of topics, which helps students see the connectedness of mathematics.

The second idea, consistent assessment, is based on the concept that testing is not really a great measure of how much a student has learned, but it actually solidifies the learning that has occurred.  So three groups of students were given different ways of learning by reading a passage of information. The first group read a passage four times. The second group read the passage three times and had test.  The third group read the passage once and was tested three times.  Their performances on tests on the information in the passage 5 minutes later and then one week later.

Diagram of retention testing research
from Roediger & Pye (2012) p.245

So if we connect the idea that testing is not the best method of seeing how much students have learned and the fact that consistent assessment actually helps students retain their knowledge, what I do in my PBL classrooms, is not only “test” but do all sort of forms of assessment (writing, oral assessment, hand-in homework with feedback, labs, quizzes, problem sets, self-assessment, etc.) alternately throughout the term.  There is probably not a week where students are not assessed in at least 2 ways. I feel that this has led students to have good retention of material and the assessments are strong measurements of their learning.

The last one was the one I was most excited to hear about – explanatory questioning.  This seemed to give students so much more responsibility for their own learning than traditional cognitive psychology as I had understood it.  The authors of this study claim that explanatory questioning can be broken in to two areas:

Elaborative Interrogation – students generating plausible explanations to statements while they are studying and learning.  This speaks directly to the idea of mathematical discussion and how students generate explanations when they ask themselves “why?”

Self-Explanation – students monitoring their learning and describing, either aloud or silently some features of their learning.  This idea can be found all over the PBL classroom but in mine, it’s generally found most in metacognitive journaling where students use self-explanation the most.

“Obviously, the elaborative interrogation and self explanation are related because both strategies encourage or even require students to be active learners, explaining the information to themselves (perhaps rephrasing in language they understand better) or asking themselves why the information is true.”

I honestly couldn’t believe what I was reading – this is an article on educational methods based on cognitive psychology that is suggesting that we require students to be active learners and “explain the infomation to themselves”?  This is lunacy.  I have been teaching for 25 years where students have been complaining to their parents that they have had to explain things to themselves – who would’ve known that I was applying cognitive psychology?

My guess is that these ideas are only enhanced by the social aspect of the classroom and other constructivist ideas – clearly the constructivitst classroom in enhanced by or agrees with some of these cognitive psychology methods as well.  Listening to both sides of the theories is actually helpful and I’m seriously going to continue doing this! Although I never thought that there might be strong connections between cognitive psychology theories and PBL, I do know that it’s life’s illusions I recall and I “really don’t know life, at all.”