James Henry Trotter: “When I had a problem, my mum and dad would tell me to look at it another way.” (Roald Dahl)

I’ve always thought that PBL fostered creative problem solving as opposed to memorization of pneumonic devices.  One of my students today proved me right when I gave a “quick quiz” on the use of the idea of tangent.  We had discussed tangent in class for only two days and in two ways – one as a slope of a line with a given angle and from that idea we discussed how it could be interpreted as the ratio of the sides of a right triangle (if you put a right triangle under the line).

Of course, during this conversation some student who had studies the ever popular SOHCAHTOA before mentioned this in class and told everyone that they had just memorized this and that’s how they knew it.  I said that’s fine but I’d like them to try to think about the context of the problems and see if this helps make any sense of it for them.

So today on the quiz one student was attempting this problem – very basic, very procedural, not at all something that I would call atypical of a textbook-like problem on tangent.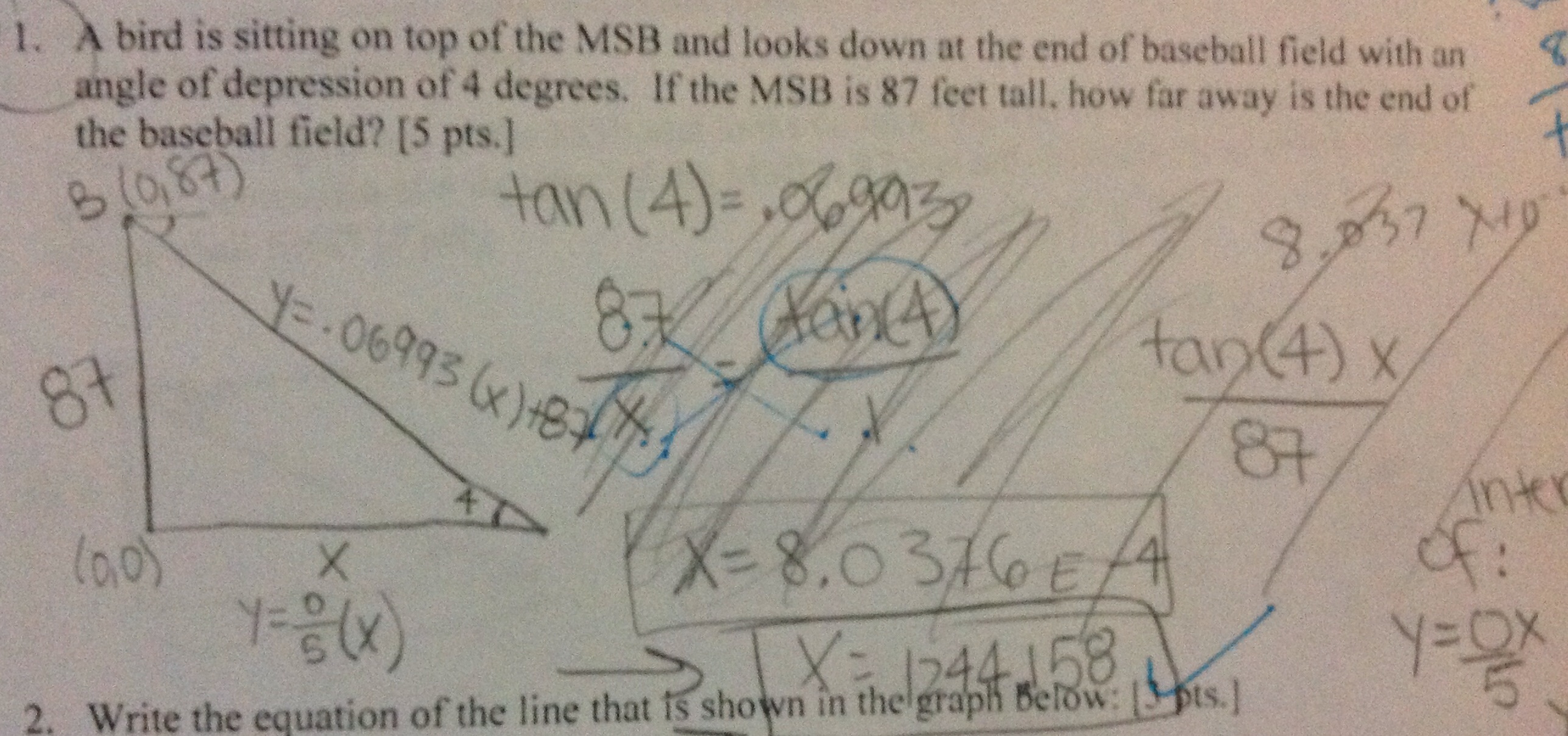

A bird is sitting on top of the Main School Building and looks down at the end of the baseball field with an angle of depression of 4 degrees.  If the MSB is 87 feet tall, how far away is the end of the baseball field?

So the student attempts to create a ratio with the sides of the triangle and even sets it up correctly.  However, because she does the algebra incorrectly, she gets an answer that is extremely small 8.037 x 10^-4.  In fact, during the quiz, she calls me over and asks what it means, she doesn’t remember scientific notation and starts getting all anxious because we didn’t do anything like this in the problems in the previous two days?  How can the answer be that small?  I said well, you better go back and think of something else.

In most classes, a student in this situation might stress out, try to do the problem over again with the limited perspective of “TOA” or of just viewing the right triangle in one way.  However, because this students had also learned other students’ perspectives of tangent as slope of a line what this girl did at this point was to see it from a different way.  Interestingly, this is what she did.  In an alternative, albeit confusing way of writing the equation of the x-axis, she wrote y=0x to represent the ground.  Then she found the tangent of 4 degrees and used that as the slope of a line.  She put the bird at the point (0,87)

She writes the equation y= – (tan4)x + 87 and explains that this is the equation of a line that makes a 4 degree angle with the x axis and has a y-intercept of 87.  Then she realizes that if she finds the intersection of that line and the x-axis, she would find how far the building is from the baseball field.  This is what she does and uses her graphing calculator to get the right answer.

When she hands in this quiz to me, I half expected that tiny little answer as her distance to the baseball field.  But what I got was an amazingly inventive solution and a correct answer.  With a problem that didn’t make sense, she looked at it a different way and ended up getting the right answer.  It was amazing what changing your perspective could do and this was great evidence that even under pressure, the habits of creativity and connection were paying off.