One of my goals in my work is often to help classroom mathematics teachers to be more deliberate in the ways in which they assess problem solving.  Although many people can be cynical about rubrics, I think that students can find them at least helpful to know what a teacher expects of them.  I have some students who told me that they pull out my rubric for grading journal writing almost every time they go to write a journal entry this fall.

However, a rubric that is vague and ambiguous about expectations can cause more harm than good.  Just throwing a rubric around that students can look at, or one that you can post on your website that you can show an administrator and say, “See, I have a rubric for that” isn’t necessarily a good thing.  Especially for problem solving.  Problem solving as a process is a very difficult thing to nail down for students especially in terms of the levels of how they can improve in their work.

I recently ran across this rubric that posted on a website under the title “Awesome Problem Solving Rubric for Teachers.”

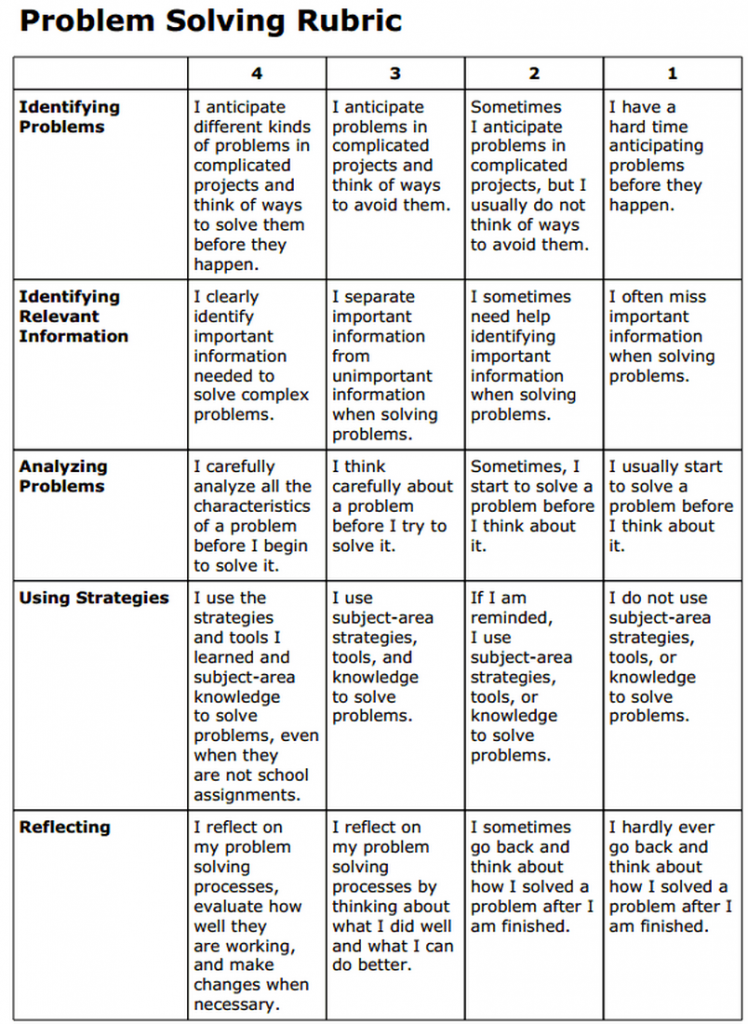
As I read through this, at first glance the categories look pretty good – Identify the problem, identify relevant information, analyze the problem, use strategies and reflect on the process.  Sounds like a pretty standard problem solving process –very similar in many ways to Polya’s process or the steps that Jo Boaler discussed in her online course How to Learn Math this summer.

The graded level descriptors of how a student might be able to see where their work “fits” in the rubric seems to only put the behaviors on a “continuum” of Always- sometimes- never instead of trying to describe actions that the student could do that describe a mediocre way of using a strategy.    For example, analyzing a problem can be so much more descriptive than just “I think carefully” about the problem before a student starts.

They could:

1. listen deliberately to others’ ideas and reflect on them in writing or verbally

2. question the given information of a problem – does it make sense in a realistic way?

3. think about the representations they can come up with for the problem – does a graphical approach make the most sense?  Why?  Would making a geometric representation be better, if so why?

4.  In comparing a new problem to ones I’ve already done, can I list the similarities and differences?  What is this question asking that others I’ve done not asked?

How many students can really ascertain what “thinking carefully” about a problem is?  I have found that more and more we need to erase as much ambiguity as possible to help students learn to be critical thinkers.  As we feel the need to teach critical thinking, reasoning skills and sense making, it is even more imperative to have rubrics that are as precise as possible.

Now, I don’t claim that mine are perfect, but my rubrics and student feedback forms have gotten some pretty good reviews from teachers and successful feedback from students.  I work on them every summer and am continually editing in order to be more deliberate about the feedback I give my students.

I also highly recommend the rubrics from the Buck Institute Website under their “tools” category.  I also adapted one of their critical thinking rubrics that was aligned to the Common Core and changed it directly for my PBL curriculum – more for presentation of problems and novel problem solving.  I’m still working on it because I have to think about exemplars for what would be above standards, but let me know if you have any feedback.

Critical Thinking rubric for PBL

So, I would just warn anyone to beware of “awesome rubrics” for teachers that they find on the internet because something that might seem awesome at first glance might end up doing more harm than good.